

【同步教案】北师大版数学七年级上册-- 第4章 基本平面图形 章末复习教案
展开第4章 基本平面图形
一、复习目标
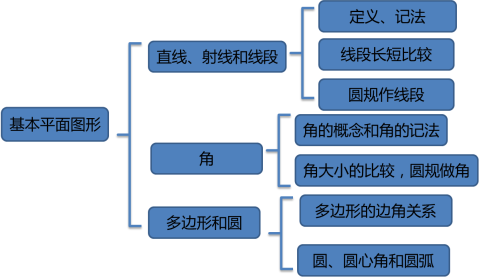
二、课时安排
2课时
三、复习重难点
(1)线段、射线和直线的概念以及线段长短的比较
(2)角的概念和角的大小比较
四、教学过程
(一)知识梳理
1.直线、射线和线段的概念。
2.如何比较线段的长短
3.角的概念
4.如何比较两个角的大小
5.多边行和圆的性质
(二)题型、方法归纳
1. 下列说法中,正确的有( )个
①过两点有且只有一条直线 ②连接两点的线段叫做两点间的距离
③两点之间,线段最短 ④若AB=BC,则点B是线段AC的中点
⑤射线AB和射线BA是同一条射线 ⑥直线有无数个端点.
A.2个 B.3个 C.4个 D.5个
2. 下列说法不正确的是( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C,三点不在一直线上,则AB<AC+BC
3. 一艘轮船行驶在B处同时测得小岛A,C的方向分别为北偏西30°和西南方向,则∠ABC的度数是( )
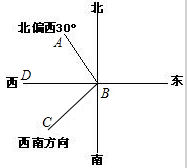
A.135° B.115° C.105° D.95°
4. 用一副三角尺,你能画出下面那个度数的角( )
A.65度 B.105度 C.85度 D.95度
5. 七边形的对角线总共有( )
A.12条 B.13条
C.14条 D.15条
(三)典例精讲
例1. 已知线段AB=6cm,在直线AB上画线段AC=2cm,则线段BC的长是多少.
![]()
![]()
解:如右图所示,可知:
①当点C在线段AB上时,BC=AB-AC=4;
②当点C在线段BA的延长线上时,BC=AB+AC=8.
例2、已知,AF平分∠BAC,DF平分∠BDC,若∠B=70°,∠C=50°,求∠AFD的度数
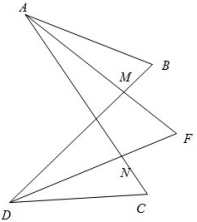
解:如图所示,设AF和BD相交于M,DF和AC相交于N,
∵∠BMF=∠B+∠BAF,∠BMF=∠F+∠FDB,
∴∠B+∠BAF=∠F+∠FDB,
∴∠BAF-∠FDB=∠F-∠B,
∵∠FNC=∠F+∠FAC,
∠FNC=∠C+∠CDF,
∴∠F+∠FAC=∠C+∠CDF,
∴∠FAC-∠CDF=∠C-∠F,
∵∠BAF=∠FAC,∠FDB=∠CDF,
∴∠BAF-∠FDB=∠FAC-∠CDF,
∴∠F-∠B=∠C-∠F,
∴2∠F=∠B+∠C=70°+50°=120°,
∴∠F=60°.
例3:如图,将圆分成A、B、C三个扇形,且半径为3 cm.
(1)求扇形C的面积;
(2)求扇形A和B圆心角的度数.
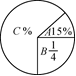
解: (1)C所占的比例是1-15%-=60%,
扇形C的面积为60%×3.14×32=16.956(cm2)。
(2)扇形A的圆心角是360°×15%=54°,扇形B圆心角是360°×=90°
(四)归纳小结
1.线段、射线和直线
直线、线段和射线的概念和记法。两点确定一条直线。
- 线段长短的比较
用圆规做一条线段等于已知线段。两点之间线段最短。线段中点的概念。
- 角的概念
角的表示:角用符号“∠”表示,常见有以方法:
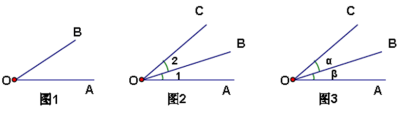
(1) 用三个大写英文字母表示:如图1,可记作∠AOB 或∠BOA,其中O 是角的顶点,必须写中间,A、B 分别是角的两边上的一点,写在两边,可以交换位置
(2) 用一个大写英文字母表示:如图1,可记作∠O。用这种方法表示的前提是同一个点作顶点的角只有一个时,否则不能用这种表示方法。如图2,∠AOC 就不能记作∠O,因为此时以O 为顶点的角不止一个,容易引起混淆。
(3) 用数字或希腊字母来表示,用这种方法表示角时,要在靠近顶点处加上弧线,注上阿拉伯数字或小写希腊字母α、β、γ等,如图2 中,∠AOB 可记作∠1,∠BOC 记作∠2,如图3 中,∠AOB 记作∠β,∠BOC 记作∠α。
把一个平角180 等分,每一份就是1 度的角,为了更精密地度量角,把1°的60 等分,每份叫做1 分的度,记作1′,又把1′的度60 等分,每一份叫做1 秒的角,记作1″。即:1°的![]() 为1分,记作1’,即1°=60’
为1分,记作1’,即1°=60’
1’的![]() 为1秒,记作1’’,即1’=60’’
为1秒,记作1’’,即1’=60’’
- 角的比较
角大小的比较方法。角的和、差、倍、分。角平分线:从一个角的顶点,引出一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
- 多边形的
多边形 | 四边形 | 五边形 | 六边形 | n边形 |
图形 |
|
|
|
|
从一个顶点发出 的对角线的条数 | 1条 | 2条 | 3条 | (n-3)条 |
分成三角 形的个数 | 2个 | 3个 | 4个 | (n-2)个 |
内角和 | 360° | 540° | 720° | (n-2)×180° |
各边相等,各角也相等的多边形叫做正多边形。
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆。固定的端点O称为圆心,线段OA称为半径。圆上任意两点A、B间的部分叫做圆弧,简称弧,记作(AB) ̂,读作“圆弧”或弧AB;由一条弧AB和经过这条弧的端点的两条半径OA、OB组成的图形叫做扇形;顶点在圆心的角叫做圆心角。
五、板书设计
1..直线、射线和线段
2.线段长短的比较
3.角的概念
4.角大小的比较
5.多边形和圆
六、作业布置
完成单元检测
七、教学反思
借助多媒体形式,使同学们能直观感受本章重点内容,以促进学生对所学知识的充分理解与掌握。采用启发、诱思、讲解和讨论相结合的方法使学生充分掌握这一章节的知识。进行多种题型的训练,使同学们能灵活运用本章重点内容。









