初中数学北师大版七年级上册5.1 认识一元一次方程精品教学设计

5.1 认识一元一次方程

一、教学目标

1、通过对多种实际问题的分析，感受方程作为刻画现实世界有效模型的意义．

2、通过观察，归纳一元一次方程的概念．

3、体验数学与日常生活密切相关，认识到许多实际问题可以用数学方法解决．

二、课时安排

1课时

三、教学重点

建立一元一次方程的概念．

四、教学难点

根据具体问题中的等量关系，列出一元次方程感受作为刻画现实世界有效模型意义．

五、教学过程

（一）情境导入

我 能猜出你们的年龄，相信吗？只要任何一个同学回答问题就马上到他是多少岁我 能猜出你们的年龄，相信吗？

问：你的年龄乘以 问：你的年龄乘以 2加 3等于多少？ 等于多少？

学生说出结果，教师猜测年龄并问：你们知道我是怎么做的吗？

学生讨论并回答

（二）讲授新课

1、小彬和明也在进行猜年龄游戏，我们来看一看

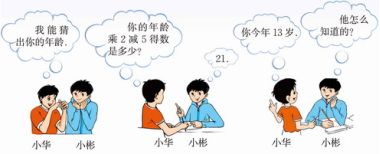
找出这道题中的等量关系，列出方程

大家观察，这个式子有什么特点？

讨论并回答：什么是方程？方程有哪些特点？

方程是含有未知数的等式。

2．判断下列式子是不方程？

（1）x＋2＝3（是） （2）x＋3y ＝6（是）

（3）3x－6（不是） （不是） （4）1＋2＝3（不是）

（5）x＋3＞5（不是） （6）y－12 ＝5（是）

3、如果告诉我们一些实际生活中的问题，大家能够自己列出方程吗？

情景一、小颖种了一株树苗，开始时树苗高位40cm，栽种后每周树苗长高约10cm。大约几周后书面长到1m？

你能找出题中的等量关系吗？怎么列方程？由此你们想到了些什么？

如果设x周后树苗长高到1m，那么可以得到方程：                  。

情景二、第五次全国人口普查统计数据（2001年3月28日）

截止2000年11月1日0时，全国每10万人中具有大学文化程度的人数为3611人，比1990年7月1日0时增长了153.94%，1990年6月底每10万人中约有多少人具有大学文化程度？

如果设2000年第五次全国人口普查时每10万人中约有x人具有大学文化程度，那么可以得到方程：                  。

情景三、西湖中学的体育场的足球场，其周长为200米，长和宽之差为12米，这个足球场的长和宽分别为多少？

如果设这个操场的宽为x米，那么长为（x+25）米，由此可以得到方程：       。

在一个方程中，只含有一个未知数，且未知数的指数都是1，这样的方程叫做一元一次方程。使方程左右两边的值相等的未知数的值，叫做方程的解。

大家刚才都已经自己列出了方程，那个同学能够说一下你是怎么样列出方程的，列方程应该分为那几步？

一、找等量关系；二、设未知数；三、列方程

（三）重难点精讲

列方程的步骤

（四）归纳小结

1、什么是方程

2、一元一次方程

3、列方程的步骤

（五）随堂检测

1、从正方形的铁皮上，截取2cm宽的一个长方形条，余下的面积是80cm2，那么原来的正方形铁皮的边长是多少？

2、已知ax2+5x+14=7x2-2x+5a是关于x的一元一次方程，则其解为   x=3．

3、已知关于y的方程3（m2-1）y2-（m-1）y+5=0是一元一次方程，则2m2-3m+1=6

六、板书设计

5.1 认识一元一次方程

概念                      例题                    练习

七、作业布置

1.家庭作业：完成本节课的同步练习；

2.预习作业：完成导学案5.2《求解一元一次方程》探究案