
北师大版七年级上册5.2 求解一元一次方程一等奖教学设计及反思
展开5.2.1 求解一元一次方程
一、教学目标
1、学会利用等式基本性质解方程;
2、理解移项的概念;
3、学会移项。
二、课时安排
1课时
三、教学重点
利用等式基本性质解方程及移项法则;
四、教学难点
利用等式基本性质来解释方程的变形.
五、教学过程
(一)情境导入
1、上节课的想一想引入新课:等式和方程之间有什么区别和联系?
方程是等式,但必须含有未知数;等式不一定含有未知数,它不一定是方程。
2、下面的一些式子是否为方程?这些方程又有何特点?
(1)、5x+6=9x ; (2)、3x+5;(3)、7+5×3=22 ;(4) 4x +3y =2.
由学生小议后回答:(1)、(4)是方程。分析这些方程得(1)等式两边都是一次式或等式一边是一次,另外一边是常数,(2)这些方程中有的含有一个未知数,有的含有两个未知数。我们先来研究最简单的(只含有一个未知数的 )的一元一次方程。
3、一次方程:我们把等号两边是一次式、或等号一边是一次式另一边是常数的方程叫做一次方程。注意:一次方程可以含有两个或两个以上的未知数:如上例的(4)。
4、复习一元一次方程和一元一次方程的解。怎么样解方程?
(二)讲授新课
1、等式性质基本性质:
(1)、等式两边同时加上(或减去)同一个代数式,所得的结果仍是等式。
(2)、等式两边同时乘同一个数(或除以同一个不为零的数),所得的结果仍是等式。
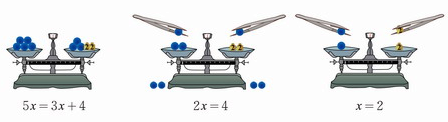
出示天平称,在天平平衡的两边同时都添上或拿去质量相同的物体,天平仍保持平衡,指出:等式也有类似的情形.
强调关键词:“两边”、“都”、“同”、“等式”.
2、利用等式基本性质解方程
例1、解方程:x+2=5
分析:要把原方程变形成x=?只要把方程两边同时减去2即可.
注意:解题格式.
例2、解方程5x=7+4x
分析:方程两边都有含x的项,要解这个方程就需要把含x的项集中到一边,即可把方程变形成x=?(一般是含x的项集中到方程的左边,使方程的右边不含有x的项),此题的关键是两边都减去4x.
(解略)
解完后提问:如何检验方程时的计算有没有错误?(由学生回答)
只要把求得的解代替原方程中的未知数,检查方程的左右两边是否相等,(由一学生口头检验)
观察前面两个方程的求解过程:
x+2=5 5x=7+4x
x=5-2 5x-4x=7
思考:(1)把+2从方程的一边移到另一边,发生了什么变化?
(2)把+4x从方程的一边移到另一边,又发生了什么变化?(符号改变)
3、移项:
从变形前后的两个方程可以看到,这种变形相当于:把方程中的某一项改变符号后,从方程的一边移到另一边,我们把这种变形叫做移项.
注意:①移项要变号;
②移项的实质:利用等式基本性质对方程进行变形.
例3、解方程:3x+4=2x+7
解:移项,得3x-2x=7-4,
合并同类项,得x=3.
∴x=3是原方程的解.
归纳:①格式:解方程时一般把含未知数的项移到方程的左边,把常数项移到方程的右边,以便合并同类项;
②解方程与计算不同:解方程不能写成连等式;计算可以写成连等式;
③一个方程只写一行,每个方程只有一个等号(理由:利用等式基本性质对方程进行变形,前后两个方程之间没有相等关系).
(三)重难点精讲
移项
(四)归纳小结
1、 等式的基本性质
2、 求解一元一次方程
3、 移项
(五)随堂检测
1、在等式-5x+3=-2的两边都加 得等式-5x=-5,然后两边都除以 ,得到x= .
2、已知(a-3)x|a|-2+6=0是关于x的一元一次方程,则方程的解为 .
3、如果3x-7=14-4x,那么 .
六、板书设计
5.2 求解一元一次方程(1)
概念 例题 练习
七、作业布置
1.家庭作业:完成本节课的同步练习;
2.预习作业:完成导学案5.2《求解一元一次方程(1)》探究案
初中数学北师大版七年级上册5.2 求解一元一次方程第3课时教学设计: 这是一份初中数学北师大版七年级上册<a href="/sx/tb_c77558_t8/?tag_id=27" target="_blank">5.2 求解一元一次方程第3课时教学设计</a>,共6页。
北师大版七年级上册第五章 一元一次方程5.2 求解一元一次方程第2课时教案及反思: 这是一份北师大版七年级上册<a href="/sx/tb_c77558_t8/?tag_id=27" target="_blank">第五章 一元一次方程5.2 求解一元一次方程第2课时教案及反思</a>,共6页。
初中数学北师大版七年级上册5.2 求解一元一次方程第1课时教案: 这是一份初中数学北师大版七年级上册<a href="/sx/tb_c77558_t8/?tag_id=27" target="_blank">5.2 求解一元一次方程第1课时教案</a>,共6页。












