初中数学北师大版八年级上册2 平方根优秀教案

6.1.3平方根

一、教学目标：

知识与技能：1、掌握平方根的概念，明确平方根和算术平方根之间的联系和区别；

2、能用符号正确地表示一个数的平方根，理解开方运算和乘方运算的互逆关系；

过程与方法:通过探索平方根和算术平方根的区别与联系，学会利用算术平方根解决平方根的问题；

情感态度与价值观：学习从特殊到一般的数学思想方法，培养学生从实践到理论，从具体到抽象的辨证唯物主义观点；

二、教学重点和难点
重点： 平方根的概念；

难点：平方根和算术平方根之间的联系和区别；

三．教学方法
1、本着以人为本的教育理念，主动地发展学生的个性特长，让学生学会学习，培养学生可持续发展学习的能力，本节课主要采用探究式和启发式的教学方法。
2、使用现代教育技术和引导学生动手实践，使学生能充实地学习数学，把注意力集中在决策、反思、归纳、推理和问题解决上。

四、教学设计：

（一）复习回顾：什么叫做算术平方根？怎么表示？有什么性质？

练：判断下列各数有没有算术平方根，如果有求出它们的算术平方根。（口答）

（1）9；（2）100；（3）；（4）0.25；（5） 0；（6）－25；

思考：因为，所以3是9的算术平方根，，叫做9的什么？

学生活动：回忆上节课内容，并完成练习.

设计意图：通过对回忆上节课内容，并完成练习.巩固上节课知识点，为学习平方根做准备.

（二）新知探索

1、概念引入：（让学生体会平方与开方的互逆关系）

     =  

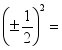
平方根：一般地，如果一个数的平方等于a,那么这个数叫做a的平方根（或二次方根）（由学生下定义，教师板书定义）

学生活动：通过感受平方与开平方的互逆过程，自己得出平方根的概念.

设计意图：通过感受平方与开平方的互逆过程，自己得出开平方运算以及平方根的概念，培养学生的分析能力以及概括能力.

例4：下列各数的平方根：（教师板书第（1）题，学生板书（2）（3）；）

（1）100；（2）；（3）0.25；

解：（1）因为，所以100的平方根是；

（2）因为，所以的平方根是；

（3）因为，所以0.25的平方根是；

学生活动：学生自己独立完成例题并且板书.

设计意图：通过对例题的解决，加深学生对新知识的理解与掌握，同时培养学生的说理能力，为以后进一步推理打下基础.

2、平方根的性质和表示

填下面表格，你发现了什么？

学生观察讨论归纳：（组内探究归纳性质）

正数有正、负两个平方根，它们互为相反数；正的平方根是它的算术平方根；

零的平方根是零；负数没有平方根；

学生活动：学生小组讨论，组内一起归纳出平方根性质.

设计意图：通过学生小组讨论，培养学生的合作探究能力，段炼学生的观察、分析、思维能力.

（三） 练习巩固，理解概念及性质

例5： 求下列各数的值；

（1）；（2）；（3）；

解：（1）因为，所以的值是；

（2）因为，所以的值是；

（3）因为，所以的值是；

学生活动：学生自己独立完成例题并且板书.

设计意图：让学生板书，一是加深学生的印象，二是培养学生的能力.

（四）小结：

（五）运用新知，体验成功

练习： 1. 下列说法正确的是（  ）

A.49的平方根是7                   B.-5是25的平方根

C.如果 有算术平方根，则  >0    D.

2.下列说法正确的是（  ）

A.平方根等于它本身的数是0和1     B.平方根等于本身的数是0

C.算术平方根等于它本身的数只有1  D.一个数一定大于它的算术平方根

3.    的平方根是      .    的平方根是      .

4.   的平方根是      .    

5.当 a=     时，     的平方根是    .

（六）课后拓展：（学生单独完成，小组讨论得出最后结果）

1.正数的两个平方根分别是和，求这个数.

 2.求下列各式中x的值：

（1）5；    (2)

（七）布置作业：必做：1-8题

                 选做：13题

五、板书设计：