


【同步教案】北师大版数学八年级上册--第三章 位置与坐标 回顾与思考教案
展开《第三章 位置与坐标回顾与思考》教学设计
【北师大版八年级上学期】
【教学内容分析】
1.课标要求
(1)结合实例进一步体会用有序数对可以表示物体的位置..
(2)了解平面直角坐标系的有关概念能画出平面直角坐标系;在给定的平面直角坐标系中,能根据坐标描出点的位置、由点的位置写出它的坐标.
(3)在实际问题中,能建立适当的直角坐标系,描述物体的位置.
(4)对给定的正方形,会选择合适的直角坐标系,写出它的顶点坐标,体会可以用坐标刻画一个简单图形.
(5)在平面上,能用方位角和距离刻画两个物体的相对位置.
2.教材分析
本节课是北师大版八年级(上)第三章《位置与坐标》的章末复习课.“图形与坐标”是“图形与几何”领域的重要组成部分,它是发展学生空间观念的重要载体.本章《位置与坐标》将引领学生感受确定物体位置方法的多样性,抽象出平面直角坐标系的概念,进而利用平面直角坐标系确定图形的位置,并从坐标的角度描述学习过的轴对称,进一步认识轴对称,将几何和代数通过点与坐标联系在一起.同时,平面直角坐标系是表示变量之间关系的重要工具,因此本章是本册下一章“一次函数”学习的重要基础,也是今后学习九上“反比例函数”、九下“二次函数”学习的重要工具..
本章所涉及的数学思想主要是数形结合思想,通过本章的学习,要让学生初步感受数形结合的思想,让学生看到平面直角坐标系的引入,架起了数与形的桥梁,加强了知识间的相互联系,它是解决数学问题的一个强有力的工具.
3.学情分析
学生七上已经学习了变量之间的关系,对平面直角坐标系不陌生,关于图形的轴对称性小学就接触过,经过这一章的学习之后,学会了在具体的问题情境中建立适当的直角坐标系,知道平面直角坐标系中的点和点的坐标是一一对应关系,认识到图形的轴对称与图形的坐标变化之间的关系.但对于坐标系内的图形变化、数量关系容易混淆,比较薄弱,缺乏综合运用知识解决较复杂问题的经验,需要进一步发展观察、归纳、类比、概括等能力,,发展有条理的思考及语言表达能力,学生的空间观念、数形结合能力、形象思维能力还有待提高.
【教学目标】
1.通过复习,掌握本章的知识网络结构及相互关系,在现实情境中能灵活运用不同的方式确定物体的位置;
2.通过复习,进一步加深对平面直角坐标系的认识,了解并掌握点的坐标及特殊的坐标特点,感受图形变换后点的坐标的变化;
3.通过总结回顾全章知识,综合运用图形与坐标的知识解决一些简单的实际问题,体会数形结合的数学思想,感受学习数学的乐趣,增强学习数学的信心.
【知识重点】
1.能结合具体情境灵活运用多种方式确定物体的位置,发展空间观念;
2.认识并能画出平面直角坐标系,会根据坐标描出点及由点的位置写出其坐标,掌握特殊位置点的坐标特点.
【教学难点】
1.能在同一直角坐标系中感受图形变化和点的坐标变化之间的关系,并会表示对称点的坐标;
2.综合运用图形与坐标的知识解决一些简单的实际问题.
【教学过程】
一.知识框架
我们前几节一起学习了第三章位置与坐标,你能否在脑海中形成一个本章知识框架图?本节课,我们一起来回顾!
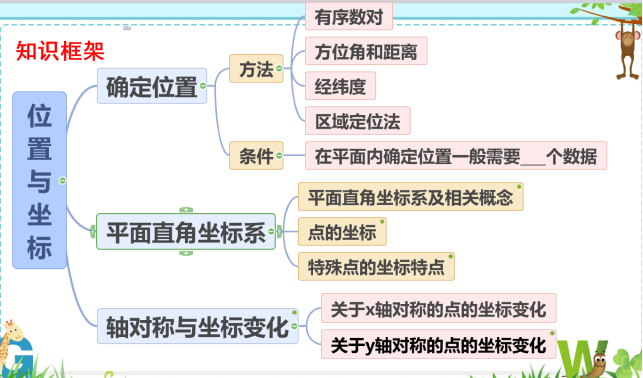 设计意图:提问并让学生回顾本章共几部分内容,每一部分下包含哪些具体知识,层层递进,让学生掌握本章的知识网络结构及相互关系. 确定位置问题引导学生在现实情境中感受确定物体位置的多种方式方法,并能灵活地运用不同的方式确定物体的位置.在学生感受了多种平面定位方式后,最后对各种定位方式的共性进行揭示:在平面内,确定一个物体的位置一般需要两个数据 .
设计意图:提问并让学生回顾本章共几部分内容,每一部分下包含哪些具体知识,层层递进,让学生掌握本章的知识网络结构及相互关系. 确定位置问题引导学生在现实情境中感受确定物体位置的多种方式方法,并能灵活地运用不同的方式确定物体的位置.在学生感受了多种平面定位方式后,最后对各种定位方式的共性进行揭示:在平面内,确定一个物体的位置一般需要两个数据 .
二.知识梳理(借助知识框架图将主要知识点逐个梳理)
1、平面直角坐标系及相关概念:
在平面内,两条互相______且具有公共______的数轴组成平面直角坐标系,其中水平方向的数轴叫______或______,取向_____为正方向;竖直方向的数轴叫_______或______,取向______为正方向两条数轴交点叫平面直角坐标系的_______,把x轴和y轴合在称之为坐标轴.
在平面直角坐标系中,两条坐标轴把平面成_______,右上方的部分叫做 ,其他三部分按逆时针方向依次叫做第二象限、第三象限、第四象限.坐标轴上的点不属于 .
2、点的坐标:
对于平面内任意一点P,过点P分别向x轴、y轴做垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的 、 ,有序数对P(a,b)叫做点P的坐标.
在平面直角坐标系中,对于平面上的任意一点,都有唯一的一个 与它对应;反过来,对于任意一个 ,都有平面上唯一的一点与它对应.坐标平面上的点与有序实数对一一对应.
点的坐标与点到坐标轴的距离关系:
点(a,b)到x轴的距离是 , 点(a,b)到y轴的距离是 .
3、特殊点的坐标特点:
各象限点的坐标特点:第一象限______,第二象限_____,第三象限______,第四象限 .
坐标轴上点的坐标特点:横轴上的点纵坐标为______,纵轴上的点横坐标为______.
与坐标轴平行的直线上的点坐标特点:平行于x轴的直线上的各点的 相等,
平行于y轴的直线上的各点的 相等.
各象限角平分线上点的坐标特点:一、三象限角平分线上的点的横纵坐标 ,
二、四象限角平分线上的点的横纵坐标 .
4、关于坐标轴对称的点的坐标特点:
图形变换与坐标变化规律:
一个图形上的点的纵坐标不变,横坐标×-1,得到的图形与原来的图形的位置关系是
一个图形上的点的横坐标不变,纵坐标×-1,得到的图形与原来的图形的位置关系是
一个图形上的点的纵坐标与横坐标同时×-1,得到的图形与原来的图形的位置关系是
关于x轴对称的两个点横坐标 ,纵坐标 .
关于y轴对称的两个点横坐标 ,纵坐标 .
设计意图:以知识框架为载体,以填空的形式给出,能够引起学生注意加深印象,逐一回忆本章知识点,使全章知识系统化、条理化、全面化 .让学生经历文字语言、图形语言、符号语言的相互转化,体验数形结合思想 .在教学过程中,教师要充分耐心倾听学生的发言,注意及时规范学生的不准确的表述 .平行于坐标轴直线上点的坐标和对称点的坐标特点用几何画板演示,形象直观,便于学生更容易理解记忆 .
三、知识应用
针对本章所学知识点,选取相应的典型题进行分类巩固.
(一)分点训练 打好基础
1.点P的坐标是(2,-3),则点P在第 象限;
若点P(x,y)的坐标满足xy <0,且在x轴上方,则点P在第 象限;
若点P(x,y)的坐标满足xy >0,则点P在第 象限.
2.若点P(x,y)在第四象限,|x|=2,|y|=3,则点P的坐标是 .
若点P(x,y)在第三象限,|x|=2,y2=9,则点P的坐标是 .
3.点A的坐标是(3,-4),到x轴的距离为 ,到y轴的距离为 .
4.点P到x轴、y轴的距离分别是2、1,则点P的坐标为 .
5.点P(a-1,a2-4)在x轴负半轴上,则P点坐标是 .
6.已知点A(1,2),直线AB∥x轴,且AB = 5,则点B的坐标为 .
7.点A(a,2a+1)在一、三象限的两坐标轴夹角的平分线上,则a= ;
点A(a,2a+1)在二、四象限的两坐标轴夹角的平分线上,则a= .
8.点(4,3)与点(-4,3)的关系是 ;点(4,3)与点(4,-3)的关系是 .
9.若点P(a,b)与点Q(1,2)关于x轴对称,a+b= ,关于y轴对称,a+b= .
(二)综合应用 思维拓展
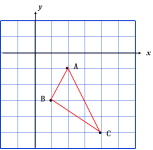 10.如图,△ABC三个顶点的坐标分别A(2,-1),B(1,-3),C(4,-5).
10.如图,△ABC三个顶点的坐标分别A(2,-1),B(1,-3),C(4,-5).
(1)已知点P是y轴上的一点,则PA+PB的最小值是 .
(2)△ABC的面积是多少?
(3)若AD平行于x轴,△ABD的面积为3,求点D的坐标.
设计意图:分点训练打好基础这一环节的试题由学生独立思考作答,有问题的由学生来讲解补充.综合应用思维拓展的试题以学生板演为主,规范解题过程.巩固学生对所学知识的进一步理解和应用,提高学生应有数学知识解决问题的能力,体会数形结合、分类讨论、割补法、方程的思想方法.
四、知识小结
通过本节课的复习,你有哪些收获?还存在哪些疑惑?
设计意图:鼓励学生大胆发言,让学生总结本节课的收获,只要正确就要给予鼓励,发展学生调理的思维能力和合理的数学表达.
五、当堂检测:
1.下列数据不能确定平面内物体位置的是( )
A.4楼9号 B.北偏东300 C.希望路25号 D.东经1180、北纬450
2.在坐标平面内,有一点P(a,b),若ab=0,那么点P的位置在( )
A.原点 B.x轴上 C.y轴 D.坐标轴上
3.若点M (a,b)在第四象限,则点M(b,a)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在直角坐标系中,已知A(1,3), B(-1,3),则下列说法正确的是( )
A.点A、B关于x轴对称 B.直线AB平行于y轴 C.A、B间的距离是2 D.A、B间的距离是6
5. 点P(a+5,a-2)在x轴上,则a =________.
6.A(8,-7)和点M关于y轴对称,则M点坐标为________.
7.在已知M(3,-4),在x轴上有一点与M的距离为5,则该点的坐标为________.
8.已知点A(2,-3)它关于x轴的对称点为A1,它关于y轴的对称点为A2,则A1、A2的位置关系是________.
9.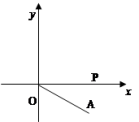 如图,坐标平面内一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的等腰三角形,那么符合条件的动点P的个数为 ________.
如图,坐标平面内一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的等腰三角形,那么符合条件的动点P的个数为 ________.
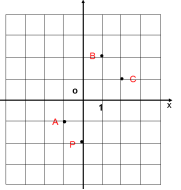 10.如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,如此下去。
10.如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次跳到点N关于点C的对称点处,…,如此下去。
(1)在图画出点M,N,并写出点M,N的坐标;
(2)求经过第2019次跳动之后,棋子落点与点P的距离。
设计意图:当堂检测旨在知识的巩固和深化,使学生反复训练本章的重要内容,同时教师可以及时地了解学生对知识的掌握情况,为下一步教学做好准备.
六、布置作业:
1.课本71页复习题的1-14.
2.拓展作业:查阅有关平面直角坐标系的相关资料,与同学分享.
设计意图:布置作业为了巩固本章所学知识,使学生深化本章的重要内容,同时检测一下学习的效果 .









