湘教版八年级上册4.1 不等式获奖教学设计

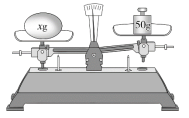
教学目标

1.了解不等式及其概念.

2.能准确运用不等式表示数量之间的不等关系.

教学重难点

重点：不等式的概念.

难点：运用不等式表示数量之间的不等关系.

教学过程

导入新课

老师展示生活中需要比较的事件的图片.

现实生活中，数量之间存在着相等与不相等的关系.对于不相等的关系问题，我们如何用式子来表示它们呢？

例如，小明的身高为155 cm，小聪的身高为156 cm，则我们可以用不等号“>”或“<”来表示他们的身高之间的关系.

如：156 > 155或155 < 156.

探究新知

1.不等式的概念

问题1：如图1所示，处于平衡状态的托盘天平的右盘放上一质量为50g的砝码，左盘放上一个圆球后向左倾斜，问圆球的质量x g与质量为50g的砝码之间具有怎样的关系？

图1

学生观察进行回答：圆球的质量大于砝码的质量，即x > 50.

问题2：一辆轿车在一条规定车速应高于60 km/h，且低于100 km/h的高速公路上行驶，如何用式子来表示轿车在该高速公路上行驶的路程s（km）与行驶时间x（h）之间的关系呢？

学生回答：根据路程与速度、时间之间的关系可得： s>60x，且s<100x.

老师提出：观察由上述问题得到的关系式：156>155，155<156，x>50，s>60x，s<100x，它们有什么共同的特点？

学生：左右不相等

归纳：像156>155，155<156，x>50，s≥60x，s≤100x 这样，我们把用不等号（>，<，≥，≤，≠）连接而成的式子叫作不等式.

例1  下列式子哪些是不等式？

（1）-3<0；（2）4x+3y>0；（3）x＝3；（4）x2+xy+y2；

（5）x≠5；（6）x+2>y+5.

解：不等式有（1）（2）（5）（6）.

2.用不等式表示数量关系

例2　用不等式表示下列数量关系：

（1）x的5倍大于-7；

（2）a与b的和的一半小于-1；

（3）长、宽分别为x cm，y cm的长方形的面积小于边长为a cm的正方形的面积.

解：（1）5x >-7；（2）；（3）xy<a2.

做一做：已知一支圆珠笔x元，签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔，若付50元仍找回若干元，则如何用含x，y的不等式来表示小华所需支付的金额与50元之间的关系？

答案：3x+10（x+y）<50

课堂练习

1.x的3倍减去2的差不大于0列出不等式是 （   　 ）

A.3x2≤0 　B.3x2≥0 

C.3x2＜0               D.3x2＞0

2.用不等式表示下列关系.

（1）x的一半不小于-1；  
（2）y与4的和大于0.5；
（3）a是负数；
（4）b是非负数.

参考答案

1.A   2.（1）0.5x≥-1. （2）y+4＞0.5. （3）a＜0 .（4）b≥0.

课堂小结

1.用不等号（>，<，≥，≤，≠）连接而成的式子叫作不等式.

2.用不等式表示数量关系.

布置作业

教材第132页习题4.1第1，2题.

板书设计

教学反思

教学反思