初中数学湘教版八年级上册4.1 不等式优质课教案

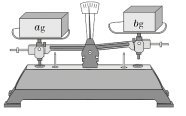
教学目标

1.掌握并能熟练应用不等式的基本性质进行不等式的变形.

2. 理解不等式的基本性质与等式基本性质之间的区别与联系. 

3.会利用不等式的基本性质将简单的不等式化为“”或“”的形式.

教学重难点

重点：不等式的基本性质2，3.

难点：不等式基本性质2，3的应用.

教学过程

导入新课

探究：用不等号填空

（1） 6＞4，6×2   4×2 ，6÷（-2）    4÷（-2）；

（2） -2＞-4，（-2）×2   （-4）×2，（-2） ÷（-2）   （-4）÷（-2）.

你能发现什么规律？

探究新知

1.不等式的基本性质2，3

让学生回答下列问题：

（1）已知苹果的价格是a元/kg，梨的价格是b元/kg，且a > b.小李各买了3 kg苹果和梨，则买哪种水果花钱较多？

用不等号填空： 3a       3b.

（2）在某次知识抢答赛中，甲、乙两队的总得分分别为a，b，其中a>b.已知每队人员均为3名，则哪队的平均得分高？

用不等号填空：a÷3        b÷3.

（3）如图1所示，托盘天平的右盘放上一质量为b g的立体木块，左盘放上一质量为a g的立体木块，天平向左倾斜.

图1

用不等号填一填：

a     b ；2a    2b；    

你发现了什么？

不等式的两边都乘（或除以）同一个正数，不等号的方向不变.

总结：

不等式的基本性质2：　不等式的两边都乘（或除以）同一个正数，不等号的方向不变.

即，如果a > b，c > 0，那么 ac > bc， > .

探究：

利用不等式的基本性质1，将不等式a>b的两边分别加上-a-b，得到-b>-a，

即（-1）×a<（-1）×b，所以不等式两边同乘-1，不等号方向改变.

猜想：不等式两边同乘一个负数，不等号方向改变.

让学生自己写一个不等式，分别在它的两边都乘或除以同一个负数，看看又是怎样的结果？与同桌互相交流，你们发现了什么规律？

总结：

不等式基本性质3   不等式的两边都乘（或除以）同一个负数，不等号的方向改变.

即，如果a > b，c < 0，那么 ac < bc，

例1　用“>”或“<”填空：

（1）已知 a>b，则3a          3b ；

（2）已知 a>b，则-a          -b .

（3）已知 a<b，则          .

解：（1）因为 a>b，两边都乘3，

由不等式基本性质2，得 3a > 3b.

（2）因为 a>b，两边都乘-1，

由不等式基本性质3，得-a<-b.

（3）因为 a<b，两边都除以-3，

由不等式基本性质3，得.

因为，两边都加2，

由不等式基本性质1，得.

利用数学上逻辑推理的方法可以得出：

不等式的性质4：如果（或），那么（或）.（对称性）

不等式的性质5：如果，，那么.（同向传递性）

补充：如果，那么，为什么？请学生思考并说明理由！

利用不等式的基本性质判断不等式的变形是否正确.

     例2　若x＜y，则下列结论中一定成立的是（　　）

A. -2+x＞-2+y  　　B.x2＜xy    C. -＞- D.x2＜y2

解析：A.因为x＜y，所以-2+x＜-2+y，所以原变形不成立，故此选项不符合题意；B.因为x＜y，所以x2＜xy（x＞0）或x2＞xy（x＜0），所以原变形不一定成立，故此选项不符合题意；C.因为x＜y，所以-＞-，所以原变形一定成立，故此选项符合题意；D.因为x＜y，所以当x＝-3，y＝1时，x2＞y2，所以原变形不一定成立，故此选项不符合题意.

答案：C

注意：判断不等式的变形是否正确时，要先观察比较已知不等式与变化后的不等式两边的变化情况，再确定应用的是不等式的哪一条基本性质，最后判断不等式的变形是否正确.

2.不等式的基本性质和等式的基本性质的联系和区别.

归纳：不等式与等式的基本性质的异同.

3.利用不等式的基本性质将简单的不等式化为“”或“”的形式.

例3　利用不等式的性质，将下列不等式化成“”或“”的形式.

（1）；        （2）；

（3）；　 　     （4）.　　　

分组活动.先独立思考，然后请4名学生上来板演，其余同学组内相互交流，最后教师作总结讲评并示范解题格式.

解：（1） ，为了使不等式中不等号的一边变为，根据不等式的性质１，不等式两边都加7，不等号的方向不变，得

                          ，    

                              .

（2），为了使不等式中不等号的一边变为，根据不等式的性质1，不等式两边都减去，不等号的方向不变.

，

.

通过（1）（2）两小题得到：解不等式时也可以“移项”，即把不等式的一边的某项变号后移到另一边，而不改变不等号的方向.

（3），为了使不等式中不等号的一边变为，根据不等式的性质2，不等式的两边都乘，不等号的方向不变，得.

（4），为了使不等式中的不等号的一边变为x，根据不等式的性质3，不等式两边都除以-4，不等号的方向改变，得.

（3）（4）的求解过程，类似于解方程两边都除以未知数的系数（未知数系数化为１），解不等式时要注意未知数系数的正负，以决定是否改变不等号的方向.来

课堂练习

    1.下列不等式的变形正确的是（　　）

A.若a＜b，且c≠0，则ac＜bc B.若a＞b，则1+a＜1+b 

C.若ac2＜bc2，则a＜b               D.若a＞b，则ac2＞bc2

2.利用不等式的性质，将下列不等式化成“”或“”的形式.

（1）；      （2）-8x ＜ 10；

（3）7-3x≤10；      （4）2x-3 ＜ 3x＋1.

参考答案

1.C　2.（1）x＜6；（2）x＞-；（3）x≥-1；（4）x＞-4.

课堂小结

1.这节课的主要内容是什么？

2.通过学习，你取得了哪些收获？

3.还有哪些问题需要注意？

让学生自己归纳，教师仅做必要的补充和点拨.

布置作业

教材第137页习题4.2第3，4，5题.

板书设计

教学反思

教学反思

教学反思

教学反思