初中数学湘教版八年级上册5.1 二次根式获奖教学设计

这是一份初中数学湘教版八年级上册5.1 二次根式获奖教学设计，共4页。教案主要包含了商的算术平方根，二次根式的除法法则，二次根式乘除混合运算等内容，欢迎下载使用。
第5章　二次根式5.2　二次根式的乘法和除法第2课时　二次根式的除法教学目标1.掌握二次根式商的算术平方根的性质，会用它进行二次根式的化简和计算.2.掌握二次根式的除法法则，能熟练地应用它进行二次根式除法运算.教学重难点重点：理解（a≥0，b>0），（a≥0，b>0）并利用它们进行计算和化简.难点：二次根式的除法运算及化简.教学过程导入新课复习引入：请同学们回答下列问题.1.写出二次根式的乘法法则及逆向等式.2.计算：（1）；（2）；（3）（xy >0）；（4）.师生活动：教师出示题目，学生独立完成.根据学生的完成情况进行讲解、强调.通过上面的复习了解同学们对二次根式的乘法的掌握情况，结合实数的乘除运算，引出本节课的课题——二次根式的除法.探究新知一、商的算术平方根问题：计算下列各式，观察计算结果，你能发现什么规律？（1）＝　　　　，＝　　　　；（2）＝　　　　，＝　　　　；（3）＝　　　　，＝　　　　.师生活动：教师出示题目，学生进行计算，并观察计算结果，总结规律，根据学生回答情况，师生共同总结得出：（a≥0，b>0）.利用它可以进行二次根式的化简.问题：在前面发现的规律中，a，b的取值范围有没有限制呢？归纳总结：二次根式商的算术平方根的性质.文字叙述：被开方数商的算术平方根等于算术平方根的商.当二次根式根号外的因数（式）不为1时，可类比单项式除以单项式法则，易得.例1　化简：（1）；（2）.解：（1）.（2）.练一练：1.能使等式成立的x的取值范围是（　）A.x≠2          B.x≥0           C.x＞2           D.x≥2 2.化简：解：.二、二次根式的除法法则把二次根式的商的算术平方根的性质反过来，就得到：一般地，二次根式的除法法则是（a≥0，b>0）.文字叙述：算术平方根的商等于被开方数商的算术平方根.当二次根式根号外的因数（式）不为1时，可类比单项式除以单项式法则，易得.例2　计算：（1）；　（2）；（3） .师生活动：教师出示题目，师生共同分析题目特点，（1）题可以直接套用二次根式的除法法则，（2）题是二次根式除法的另一种表示方法，可以直接套用除法法则进行解题.找两个学生板演解题过程，其他同学做在练习本上.解：（1）；（2）；（3）.注意：（1）除式是分数或分式时，先要转化为乘法再进行运算.（2）被开方数中含有带分数，应先将带分数化成假分数，再运用二次根式除法法则进行运算.三、二次根式乘除混合运算二次根式的乘除混合运算按照从左到右的顺序进行计算，如果有括号，应先算括号里面的.在二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式.例3　计算：.解：＝ ＝.课堂练习1.化简 的结果是（　　）A.9         　 B.3         　 C.           D.  2.下列各式的计算中，结果为 的是（　　）A.                   B. C.                   D. 3.若使式子成立，则实数k的取值范围是（　　）A.k≥1        B.k≥2   　　　　C. 1＜k≤2       D. 1≤k≤2 4.化简：（1）；（2）；（3）.参考答案1.B　2.C　3.B　4.解：（1）.（2）.（3）.课堂小结教师和学生一起回顾本节课所学内容，并请学生回答以下问题：（1）二次根式的除法法则是什么？商的算术平方根的性质表示为　　　　　　　.（2）在二次根式除法计算、化简时要注意什么？布置作业教材第164页练习习题5.2第2，3题.板书设计5.2　二次根式的乘法和除法（第2课时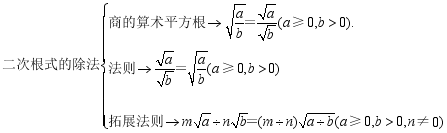） 例1　　　　　　　　例2            例3教学反思                         教学反思                              教学反思                              教学反思