【同步教案】苏教版数学五年级上册--2.5梯形的面积练习 教案

年级

五

学科

数学

主题

梯形的面积练习

主备教师

课型

新授

课时

1

时间

导学教师

教学目标

1、使学生通过实际问题的解答，进一步巩固梯形的面积公式，能应用公式正确计算平行四边形和梯形的面积，解决生活中的实际问题。

2. 使学生经历观察、操作、测量、填表、讨论、推理等数学活动过程，进一步体会转化的思想方法，培养空间观念，发展初步的逻辑思维。

3、使学生在解决实际问题的过程中中，进一步增强与同伴合作交流的意识，增强探索学习的兴趣和信心。

教学

重、难点

教学重点：通过实际问题的解答，进一步巩固梯形的面积公式，能应用公式正确计算平行四边形和梯形的面积，解决生活中的实际问题。

教学难点：巩固梯形的面积公式，

导学方法

引导学生在经历解决生活中实际问题的过程，进一步巩固梯形的面积公式，能应用公式正确计算梯形的面积，解决生活中的实际问题。

导学步骤

导学行为（师生活动）

设计意图

导学教师复备

回顾旧知，引出新课

一、导入新课

复习：

1、三角形的面积和梯形计算方法是什么？是怎样研究的？

2、在下面的图形中，你会求哪些图形的面积？

这节课我们一起来进行梯形的面积的练习。

通过谈话激发学生的学习兴趣。

新知探索

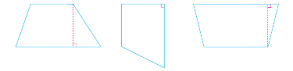
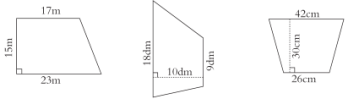
例题

精讲

二、基本练习

1、量出每个梯形的上底、下底和高，算出面积

指一指每个图形的底和高分别在什么位置，再说说测量的结果，然后再计算。

生独立完成后交流：

小结：要想求梯形的面积，需要测量出梯形的上底和下底，中间的梯形是直角梯形，直角梯形中与上底和下底垂直的那条腰的长度就是梯形的高；三个图形的上底、下底和高依次是：2厘米，4厘米，2厘米；2厘米，3厘米，2厘米；4厘米，3厘米，2厘米。

2、水渠的横截面积与拦河坝的横截面的形状如下图：你能分别算出水渠与拦河坝的横截面的面积吗？

先说说水渠和拦河坝的横截面分别是指图中的哪个部分？图中标出的条件各是梯形的什么？

生独立完成后交流

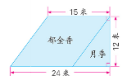
3、一个梯形花坛，分成了一个平行四边形和一个三角形，分别种了郁金香和月季（如下图）这两种花占地面积各是多少？

花坛是由左边的平行四边形和右边的三角形组合而成的，先说说图中平行四边形和三角形的底和高各是多少？

小结：平行四边形的底是15米，与之相对应的高是12米；右边的三角形是直角三角形，它的两条直角边就是一组底和高，分别是9米、12米。

生独立解答后交流算式。

三、回顾总结：

在计算梯形的面积时，先找出它们的上底、下底和高，注意它们的底和高必须是相对应的，在计算梯形的面积时，一定不要忘记除以2。

让学生通过画梯形了解梯形的面积与什么有关。

让学生了解

在求梯形的面积时应注意的问题。

课堂检测

四、自主练习：

1、一块白菜地的形状是梯形，上底是9米，下底是12米，高是18米。如果平均每棵白菜占地9平方分米，这块地一共可以种白菜多少棵？

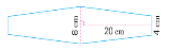
2、“银苏号”滑翔机的尾翼是由两个完全相同的梯形组成的，它的面积是多少？

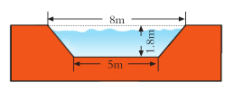
小结：滑翔机模型的尾翼是由两个完全一样的梯形组合而成的，计算它的面积，可先算出一个梯形的面积，再乘2；也可以把这两个梯形拼成一个平行四边形再计算面积，列式为：（8+4）×20。

3、某水渠的横截面是梯形。渠口宽8米，渠底宽5米。渠深1.8米。求它的横截面面积。

课堂练习的巩固梯形的面积的计算方法。

总结提升

课堂小结：

谈谈你这节课的收获：

板书设计

梯形的面积的练习

在计算梯形的面积时，先找出它们的上底、下底和高，注意它们的底和高必须是相对应的，在计算梯形的面积时，一定不要忘记除以2。

本课作业

1、   （48+96）×12÷18        132+25×（40-4）

2、   计算下面梯形的面积

本课教育评注（实际教学效果及改进设想）