


初中数学北师大版七年级上册2.5 有理数的减法精品一课一练
展开
2.5有理数的减法
一、选择题
1.计算:![]() ,结果是( )
,结果是( )
A.0 B.6 C.-6 D.9
2.2022年2月5日,杭州某区最高气温为8℃,最低气温为-1℃,那么这天的最高气温比最低气温高( )
A.7℃ B.-7℃ C.9℃ D.-9℃
3.A为数轴上表示 3的点,将点A沿数轴平移7个单位到点 B,则点B表示的数是( )
A.4 B.10 C.-4 D.-4或10
4.如图,![]() 、
、![]() 是数轴上的两个数,则
是数轴上的两个数,则![]() 一定是( )
一定是( )
![]()
A.负数 B.0 C.整数 D.正数
5.若|a|=3,|b|=4,且a+b>0,则a-b的值是( )
A.-1或-7 B.-1或7 C.1或-7 D.1或7
6.绝对值是![]() 的数减去
的数减去![]() 所得的差是( )
所得的差是( )
A.![]() B.-1 C.
B.-1 C.![]() 或-1 D.
或-1 D.![]() 或1
或1
7.北京与西班牙的时差为7个小时.比如,北京时间中午12点是西班牙的凌晨5点,2022年2月4日晚8时北京冬奥会开幕式正式开始,在西班牙留学的嘉琪准时观看了直播,直播开始的当地时间为( )
A.凌晨1点 B.凌晨3点 C.17:00 D.13:00
8.计算![]() 的结果是( )
的结果是( )
A.1 B.-1 C.5 D.-5
9.下面说法中正确的有( )
(1)一个数与它的绝对值和一定不是负数;(2)一个数减去它的相反数,它们的差是原来的2倍;(3)零减去一个数一定是负数;(4)正数减负数一定是负数;(5)数轴上原点两侧的数互为相反数
A.2个 B.3个 C.4个 D.5个
10.已知a是最大的负整数,b是绝对值最小的整数,c是最小的正整数,则|a+b-c|等于()
A.-1 B.1 C.0 D.2
11.已知实数a,b在数轴上的位置如图所示,下列结论中错误的是( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.计算:![]() ______.
______.
2.珠穆朗玛峰的海拔高度是8848.43m,吐鲁番盆地海拔高度为![]() 米,珠穆朗玛峰的海拔高度比吐鲁番盆地海拔高度高______米.
米,珠穆朗玛峰的海拔高度比吐鲁番盆地海拔高度高______米.
3.在数轴上,与表示![]() 的点的距离是4的数为__.
的点的距离是4的数为__.
4.有理数x和y在数轴上的位置如图所示,则![]() ________0.(填<,>号)
________0.(填<,>号)
![]()
5.已知![]() ,且
,且![]() ,则x—y=______.
,则x—y=______.
6.如果全班某次数学测试的平均成绩为90分,某位同学考了93分,记作+3分,那么得分86分应记作______.
7.某天温度最高是8℃,最低是-9℃,这一天日温差是______℃.
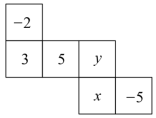
8.如图,是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x-y=_____.
9.已知|x|=1,|y|=3,若![]() ,则x-y=____
,则x-y=____
10.数轴上表示点A的数是最大的负整数,则与点A相距4个单位长度的点表示的数是_______.
11.a、b、c在数轴上的位置如图所示:
a-b___0 ; b-c ___0 ; -b-c___0 ; a-(-b)_____0 (填>,<,=)
![]()
三、解答题
1.计算 ![]() .
.
2.下表是某班5名同学某次数学测试成绩.根据信息完成下表,并回答问题.
姓名 | 王芳 | 刘兵 | 张昕 | 李聪 | 江文 |
成绩 | 89 |
|
| 84 |
|
与全班平均分之差 |
|
| 0 |
|
|
五人中分数最高的是谁?谁的分数与全班平均分最接近?
3.我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离.若点M表示的数m,点N表示的数是n,点M在点N的右边(即![]() ),则点M,N之间的距离为
),则点M,N之间的距离为![]() ,即
,即![]() .
.
(1)数轴上表示2和7的两点之间的距离是_______;数轴上表示![]() 和7的两点之间的距离是_______.
和7的两点之间的距离是_______.
(2)若数轴上分别表示m和![]() 的两点A和B之间的距离
的两点A和B之间的距离![]() ,求m的值.
,求m的值.
4.已知![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
5.若a,b,c是有理数,|a|=3,|b|=10,|c|=5,且 a,b异号,b,c 同号,求a-b-(-c)的值.
6.已知M,N都为数轴上的点,当M,N分别表示下列各数时:
①+3和+6;②-3和+6;③3和-6;④-3和-6.
(1)请你分别求点M,N之间的距离.
(2)根据(1)的求解过程,你能从中得出求数轴上任意两点间的距离的规律吗?试试看.
7.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:![]() )依先后次序记录如下:
)依先后次序记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)出租车在行驶过程中,离鼓楼最远的距离是多少?
(3)出租车按物价部门规定,起步价(不超过![]() 千米)为
千米)为![]() 元,超过
元,超过![]() 千米的部分每千米的价格为
千米的部分每千米的价格为![]() 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少?
答案
一、选择题
B.C.D.D.A.C.D.A.A.D.C
二、填空题
1.![]() .
.
2.9003.43.
3.1或![]() .
.
4.<
5.1或9.
6.![]()
7.17.
8.5
9.-2或-4.
10.![]() 或3.
或3.
11.>;>;>;<.
三、解答题
1.解:原式=![]()
=![]()
=![]()
=![]()
2.解:全班平均分为:84-(-6)=90(分)
王芳的测试成绩与全班平均分之差为:89-90=-1(分);
刘兵的数学测试成绩为:90+(+2)=92(分);
张昕的数学成绩为:90+0=90(分);
江文的数学成绩为:90+(-2)=88分;
完成表格得
姓名 | 王芳 | 刘兵 | 张昕 | 李聪 | 江文 |
成绩 | 89 | 92 | 90 | 84 | 88 |
与全班平均分之差 | -1 | +2 | 0 | -6 | -2 |
故答案为分数最高的是刘兵,分数最低的是李聪,张昕的分数与全班平均分最接近.
3.(1)
解:数轴上表示2和7的两点之间的距离是:7−2=5;
数轴上表示−2和7的两点之间的距离是:7−(−2)=7+2=9;
故答案为:5;9.
(2)
解:当点A在点B的左侧时,m=−2−24=−26;
当点A在点B右侧时,m=−2+24=22;
故m的值为−26或22.
4.(1)
∵|x|=3,|y|=2
∴![]()
∵x>0,y<0
∴x=3,y=-2,
∴x+y=3+(-2)=1;
所以x+y的值为1;
(2)
由|x|=3,|y|=2.x<y,可得x=-3,y=2或x=-3,y=-2,
当x=-3,y=2时,x-y=-3-2=-5,
或x=-3,y=-2时,x-y=-3-(-2)=-1,
所以x-y的值为-5或-1.
5.因为|a|=3,所以a=3或a=-3.
因为|b|=10,所以b=10或b=-10.
因为|c|=5,所以c=5或c=-5.
又因为a,b 异号,b,c 同号,
所以a=-3,b=10,c=5或a=3,b=-10,c=-5.
当a=-3,b=10,c=5时,a-b-(-c)=-3-10-(-5)=-8 ;
当a=3,b=-10,c=-5时, a-b-(-c)=3-(-10)- 5=8.
所以a-b-(-c)的值为8或-8.
6.如图.
![]()
(1)①点M,N之间的距离为|6|-|3|=6-3=3.
②点M,N之间的距离为|6|+|-3|=6+3=9.
③点M,N之间的距离为|-6|+|3|=6+3=9.
④点M,N之间的距离为|-6|-|-3|=6-3=3.
(2)能.在(1)中,①可以写成|6|-|3|=|6-3|=3;②可以写成|6|+|-3|=|6-(-3)|=9;③ 可以写成|-6|+|3|=|-6-3|=9;④可以写成|-6|-|-3|=|-6-(-3)|=3,
所以点M,N之间的距离为这两个点所表示的数的差的绝对值.
故求数轴上任意两点间的距离可以转化为求这两点在数轴上所表示的数的差的绝对值.
7.(1)+9﹣3﹣5+4﹣8+6﹣3﹣6﹣4+10=0.
故出租车离鼓楼出发点0km,出租车在鼓楼;
(2)+9﹣3=6,6﹣5=1,1+4=5,5﹣8=﹣3,﹣3+6=3,3﹣3=0,0﹣6=﹣6,﹣6﹣4=﹣10,﹣10+10=0.
故离鼓楼最远的距离是10km;
(3)﹙|+9|+|﹣3|+|﹣5|+|+4|+|﹣8|+|+6|+|﹣3|+|﹣6|+|﹣4|+|+10|﹣3×10﹚×1.4+8×10=39.2+80=119.2(元).
故司机一个下午的营业额是119.2元.
初中数学北师大版七年级上册2.5 有理数的减法复习练习题: 这是一份初中数学北师大版七年级上册<a href="/sx/tb_c9912_t7/?tag_id=28" target="_blank">2.5 有理数的减法复习练习题</a>,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版七年级上册2.5 有理数的减法达标测试: 这是一份北师大版七年级上册<a href="/sx/tb_c9912_t7/?tag_id=28" target="_blank">2.5 有理数的减法达标测试</a>,共4页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级上册2.5 有理数的减法综合训练题: 这是一份初中数学北师大版七年级上册2.5 有理数的减法综合训练题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













