初中数学北师大版七年级上册3.5 探索与表达规律精品达标测试

3.5探索与表达规律

一、选择题

1．观察下列算式，，，，，，，，，用你所发现的规律得出的末位数字是（   ）

A．2 B．4 C．6 D．8

2．一列数1，2，2，3，3，3，4，4，4，4，…中的第35个数为（    ）

A．6 B．7 C．8 D．9

3．观察下列等式：，，，，…，则（    ）

A． B． C． D．

4．下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律则第㊴个图形中小圆圈的个数为（    ）

A．120 B．123 C．126 D．129

5．如图，是一个运算程序的示意图，若开始输入x的值为625，则第2021次输出的结果为（　　）

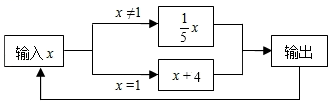
A．5 B．1 C．25 D．625

6．根据下图数字之间的规律，问号处应填（    ）

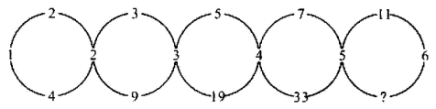
A．65 B．61 C．43 D．37

7．生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n来表示．即：21＝2，22＝4，23＝8，24＝16，25＝32，……，请你推算22022的个位数字是（    ）

A．8 B．6 C．4 D．2

8．如图所示的是中国南宋数学家杨辉在详解《九童算法》中出现的三角形状的数列，又称为“杨辉三角”．该三角形中的数据排列有着一定的规律，第21行从左边数第19个数是（     ）

A．19 B．380 C．210 D．190

9．观察图中正方形四个顶点所标的数字规律，可知数2022应标在（  ）

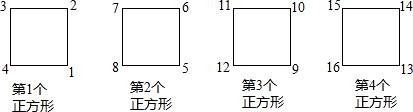
A．第506个正方形的右上角 B．第506个正方形的左下角

C．第505个正方形的右上角 D．第505个正方形的左下角

二、填空题

1．我们知，3的正整数次幂：31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561，……，观察归纳，可得32007的个位数字是___________．

2．下面是按一定规律排列的一列数：2，5，10，17，…，则第n个数是 _______．

3．观察下列等式：

①13=12；

②13+23=32；

③13+23+33=62；

④13+23+33+43=102；

根据此规律，13+23+33+···+73的结果为_______．

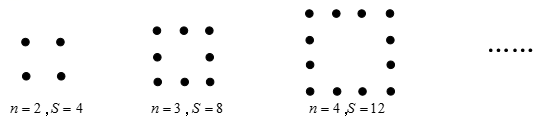
4．观察下面的图案，每条边上有个点，每个图案中点的总数是S．第2021个图形中，S的值为__________．

5．有一列数，…，那么第n个数为______．

6．找出下列数的规律：，，，，， ______ ．

7．观察下列一组数：1，2，2，3，3，3，4，4，4，4，5，5，5，5，5，6，…其中每个数n都连续出现n次，那么这一组数的第99个数是 _____．

8．将全体正整数排成一个如下图的数阵，根据上述排列规律，数阵中2022排在第_______行第_______列．

9．如图所示，下列图形都是由面积为1的正方形按一定的规律组成，其中，第1个图形中面积为1的正方形有2个，第2个图形中面积为1的正方形有5个，第3个图形中面积为1的正方形有9个……按此规律，则第7个图形中面积为1的正方形的个数为___________．

10．观察下列图形：

它们是按一定规律排列的，依照此规律，第15个图形共有_______个★．

11．用同样规格的黑白两种颜色的正方形，按如图的方式拼图，请根据图中的信息完成下列的问题．

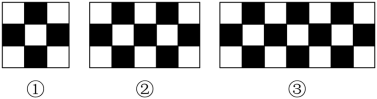
(1)在图②中用了________块黑色正方形，在图③中用了________块黑色正方形；

(2)按如图的规律继续铺下去，那么第个图形要用________块黑色正方形；

(3)白色正方形足够多的情况下，小明同学说，他恰好用完了块黑色正方形，拼出具有以上规律的图形，请问此时是第________个图形．

三、解答题

1．（1）观察下列各式：

根据你发现的规律回答下列问题：

①的个位数字是___________；的个位数字是___________；

②的个位数字是___________；的个位数字是___________；

（2）自主探究回答问题：

①的个位数字是___________，的个位数字是___________；

②的个位数字是___________，的个位数字是___________．

（3）若n是自然数，则的个位上的数字（    ）

A．恒为0          B．有时为0，有时非0       

C．与n的末位数字相同      D．无法确定

2．观察下面三行数：

1，4，9，16，25，…；①

3，2，11，14，27，…；②

3，，27，48，75，…；③

（1）第①行第6个数是_________；第②行第7个数是____________；第③行第8个数是________；

（2）已知123是其中某一行的某一个数，则它是第________行的第__________个数；

（3）取每行数的第100个数，求这三个数的和．

3．仔细观察下列等式：

第1个：52﹣12=8×3

第2个：92﹣52=8×7

第3个：132﹣92=8×11

第4个：172﹣132=8×15

…

(1)请你写出第6个等式：　　　　；

(2)请写出第n个等式：　　　　；

(3)运用上述规律，计算：8×7+8×11+…+8×399+8×403．

4．仔细观察下列三组数：

第一组：1，﹣4，9，﹣16，25，……

第二组：0，﹣5，8，﹣17，24，……

第三组：0，10，﹣16，34，﹣48，……

根据它们的规律，解答下列问题：

(1)取每组数的第10个数，计算它们的和；

(2)取每组数的第n个数，它们的和能否是﹣1，说明理由．

5．阅读探究：，，，…

(1)根据上述规律，小亮发现，求出___________．

(2)小聪继续又发现：

，求出___________．

(3)若，请运用小聪的方法求和的值

6．阅读下面材料并完成填空：

你能比较两个数20162017和20172016的大小吗？为了解决这个问题先把问题一般化，要比较nn＋1和（n＋1）n的大小（的整数），先从分析n＝1，＝2，＝3，……这些简单的情况入手，从中发现规律，经过归纳，猜想出结论．

(1)通过计算，比较下列①—⑦各组中两个数的大小（在横线上填“＞、＝、＜”号

①12        21；②23        32；③34        43；

④45        54；⑤56        65；⑥67        76；

⑦78        87．

(2)对第（1）小题的结果进行归纳，猜想出nn＋1和（n＋1）n的大小关系：        ．

(3)根据上面的归纳结果猜想得到的一般结论是：20162017        20172016．

答案

一、选择题

C．C．B．A．A.B.C．D．A

二、填空题

1.7

2.n2+1．

3.784．

4.8080

5.

6.．

7.14．

8.59；6

9.35

10.．

11.(1)7，10

(2)

(3)13

三、解答题

1.解：（1）①

3的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环

的个位数字是9；

13的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环

的个位数字是7；

故答案为：9；7；

②由①可知尾号为3的数的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环

的个位数字是7，的个位数字是7；

故答案为：7；7；

（2）①

7的乘方的个位数字依次是7，9，3，1，以此4个数为一个循环依次进行循环

的个位数字是3，的个位数字是3

故答案为：3；3

②

2的乘方的个位数字依次是2，4，8，6，以此4个数为一个循环依次进行循环

52的乘方的个位数字依次是2，4，8，6，以此4个数为一个循环依次进行循环

的个位数字是8，的个位数字是8

故答案为：8；8

（3）由（1）（2）中的结论可知与个位上的数字相同

的个位上的数字恒为0

故选A．

2.解：（1）第①行是以从1开头的的自然数的平方，奇数位置为负，偶数位置为正；

∴第①行第6个数是；

第②行是再第①行的基础上减去2，

∴第②行第7个数是；

第③行是再第①行的基础上乘以得到的，

∴第③行第8个数是，

故答案为：36，-51，-192；

（2）∵，，

当时，，

∴它是第②行第个数，

故答案为：②，11；

（3）解：这三个数的和是：

．

3.(1)

解：根据式子的特点，可知第6个等式是：252﹣212=8×23．

故答案为：252﹣212=8×23；

(2)

解：第n个等式是：（4n+1）2﹣（4n﹣3）2=8（4n﹣1）．

验证：左边=（4n+1）2﹣（4n﹣3）2

=16n2+8n+1﹣16n2+24n﹣9

=32n﹣8

=8（4n﹣1）

=右边；

(3)

解：8×7+8×11+…+8×399+8×403

=92﹣52+132﹣92+…+4012﹣3972+4052﹣4012

=4052﹣52

=（405+5）（405﹣5）

=410×400

=164000．

4.（1）

解：第一组：∵1=（-1）1+1×12，

-4=（-1）1+2×22，

9=（-1）1+3×32，

-16=（-1）1+4×42，

25=（-1）1+5×52，

…，

∴第n个数为：（-1）n+1n2；

第二组：0=1-1，-5=-4-1，8=9-1，…，

则第n个数为：（-1）n+1n2-1；

第三组：0=0×（-2），10=-5×（-2），-16=8×（-2），…，

则第n个数为：-2×[（-1）n+1n2-1]；

第一组第10个数为：（-1）10+1×102=-100，

第二组第10个数为：-100-1=-101，

第三组第10个数为：-101×（-2）=202，

∴这三个数的和为：-100+（-101）+202=1．

（2）

解：每组第n个数依次为：、、，

∴

=

=1，

故取每组数的第n个数，它们的和能否是1，不能是-1．

5.（1）

解：∵，，，

∴，

∴

故答案为：6

（2）

解：∵，

，

∴，

∴.

故答案为：7

（3）

解：∵，

∴

∵，

∴，.

6.（1）

①∵12=1，21=2，

∴12＜21；

②∵23=8，32=9，

∴23＜32；

③∵34=81，43=64，

∴34＞43；

④∵45=1024，54=625，

∴45＞54；

⑤∵56=15625，65=7776，

∴56＞65；

⑥∵67=279936，76=117649，

∴67＞76；

⑦∵78=5764801，87=2097152，

∴78＞87；

（2）

当n＝1或2时，nn＋1＜（n＋1）n；

当n＞2的整数时，nn＋1＞（n＋1）n；

（3）

根据第（2）小题的结论可知，20162017＞20172016．