初中5.6 应用一元一次方程——追赶小明精品课后复习题

这是一份初中5.6 应用一元一次方程——追赶小明精品课后复习题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
5.6应用一元一次方程—追赶小明  一、选择题1．我国古代有一问题：跑得快的马每天走240里，跑得慢的马每天走150里，慢马先走12天，快马几天可以追上慢马？如果设快马x天可追上慢马，下面所列方程中正确的是(    )A． B．C． D．2．《九章算术》是中国古代的一部数学专著，其中记载了一道有趣的题：“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”大意是：今有野鸭从南海起飞，7天到北海；大雁从北海起飞，9天到南海．现野鸭从南海、大雁从北海同时起飞，问经过多少天相遇？设经过x天相遇，根据题意可列方程为（   ）A． B． C． D．3.两地相距千米，甲从地步行到地，乙从地步行到地，甲比乙晚出发小时，乙出发小时后两人在途中相遇，已知甲每小时比乙多走千米，设甲每小时走千米．根据题意可得方程（  ）A． B．C． D．4．我国元代朱世杰所著的《算学启蒙》一书中，有一道题目是“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之．”译文：跑得快的马每日走240里，跑得慢的马每日走150里，慢马先走12天，快马几天可以追上慢马？则下列回答正确的是（    ）．A．15天 B．16天 C．18天 D．20天5．我国古代有很多经典的数学题，其中有一道题目是：良马日行二百里，驽马日行一百二十里，驽马先行十日，问良马几何追及之．意思是：跑得快的马每天走200里，跑得慢的马每天走120里，慢马先走10天，快马几天可追上慢马？若设快马天可追上慢马，则由题意可列方程为（    ）A． B．C． D．6．李华和赵亮从相遇20千米的A、B两地同时出发相向而行，李华每小时走3千米，2小时后两人相遇，设赵亮的速度为x千米每小时，列方程得（    ）．A．2x+3=20 B．+x=20C．2(3+x)=20 D．2(x-3)=207．某中学学生军训，沿着与笔直的铁路并列的公路匀速前进，每小时走4.5千米．一列火车以每小时120千米的速度迎面开来，测得从火车头与队首学生相遇，到车尾与队末学生相遇，共经过12秒．如果队伍长150米，那么火车长（　　）A．150 米 B．215米 C．265 米 D．310米8．甲、乙两地相距270千米，从甲地开出一辆快车，速度为120千米/时，从乙地开出一辆慢车，速度为75千米/时．如果两车相向而行，慢车先开出1小时后，快车开出，那么再经过多长时间两车相遇？若设再经过x小时两车相遇，则根据题意可列方程为（　　）A．75＋（120－75）x＝270 B．75＋（120＋75）x＝270C．120（x－1）＋75x＝270 D．120×＋（120＋75）x＝2709．运动场环形跑道周长400米，小林跑步的速度是爷爷的倍，他们从同一起点沿跑道的同一方向同时出发，5min后小林第一次与爷爷相遇，小林跑步的速度是（      ）米/分．A．120 B．160 C．180 D．200二、填空题1．小明早上骑自行车上学，中途因道路施工推车步行了一段路，到学校共用时16分钟，如果他骑自行车的平均速度是每分钟240米，推车步行的平均速度是每分钟80米，他家离学校的路程是3000米，设他推车步行的时间为x分钟，则可列方程______． 2．甲、乙两人同时同向环湖竞走，环湖一周400m，乙的速度是80m/min，甲的速度是乙的速度的，且甲在乙前100m，______分钟后，两人第一次相遇。3．A、B两地相距300千米，一列慢车从A地开出，每小时行60千米，一列快车从B地开出，每小时行80千米．（1）两车同时开出，相向而行，x小时相遇，则由此条件列出的方程是____________；（2）两车同时开出，同向而行，慢车在快车后面，x小时后快车与慢车相距800千米，则由此条件列出的方程是______________． 4．甲､乙两人骑自行车同时从相距的两地相向而行，已知甲每小时行驶，乙每小时行驶，则他们________后相遇． 5．小杰，小丽两人在400米的环形跑道上练习跑步，小杰每分钟跑300米，小丽每分钟跑150米，两人同时同地同向出发，__分钟后两人第一次相遇． 6．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行八十步，善行者追之，问几何步及之？”其意思为：速度快的人走100步，速度慢的人只走60步，现速度慢的人先走80步，速度快的人去追赶，则速度快的人要走______步才能追到速度慢的人．7.《九章算术》标志着中国古代数学体系的形成，全书收集了246条经典数学题．在第六章《均输》中有这样一条题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”你能算出____________步及之．8．甲、乙两人分别从A、B两地同时相向匀速前进，在距A点700米处第一次相遇，然后继续前进，甲到A地、乙到B地后都立即返回，第二次相遇在距B点400米处，则A、B两地间的距离是_____米．三、解答题1．甲、乙两人在环形跑道上练习跑步，已知环形跑道一圈长400米，乙每秒跑6米，甲每秒跑8米．(1)如果甲、乙两人在跑道上相距8米处同时反向出发，那么经过多少秒两人首次相遇?(2)如果甲在乙前面8米处同时同向出发，那么经过多少秒两人首次相遇?      2．“今有善行者行一百步，不善行者行六十步．”（出自《九章算术》）意思是：同样时间段内，走路快的人能走100步，走路慢的人只能走60步．假定不善行者步长是善行者步长的1.5倍，据此回答以下问题：今不善行者先行两百步，善行者追之，问几何步及之？即：走路慢的人先走200步，请问走路快的人走多少步才能追上走路慢的人？       3．甲、乙两车分别从相距240 km的 A、B两地出发，沿足够长的公路行驶，甲车速度为72 km/h，乙车速度为48 km/h．(1)两车同时出发，相向而行，设x h相遇，可列方程     ．解方程得    ．(2)两车同时出发，同向而行(乙车在前甲车在后），若设yh相遇，列方程   ；解方程得   ．(3)两车同时出发，同向而行，多长时间后两车相距120 km？      4．甲、乙两城相距800千米，一辆客车从甲城开往乙城，车速为千米小时，同时一辆出租车从乙城开往甲城，车速为90千米小时，设客车行驶时间为小时当时，客车与乙城的距离为多少千米用含a的代数式表示已知，丙城在甲、乙两城之间，且与甲城相距260千米求客车与出租车相距100千米时客车的行驶时间；列方程解答已知客车和出租车在甲、乙之间的服务站M处相遇时，出租车乘客小王突然接到开会通知，需要立即返回，此时小王有两种返回乙城的方案：方案一：继续乘坐出租车到丙城，加油后立刻返回乙城，出租车加油时间忽略不计；方案二：在M处换乘客车返回乙城．试通过计算，分析小王选择哪种方案能更快到达乙城？       5．一辆车长为4米的小轿车和一辆车长为20米的大货车，在长为1200米隧道的两个入口同时开始相向而行，小轿车的速度是大货车速度的3倍，大货车速度为10米/秒．(1)求两车相遇的时间；(2)求两车从相遇到完全离开所需的时间；(3)当小轿车车头和大货车车头相遇后，求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间．                                      答案一、选择题A.A．A.D．D．C．C．B.D．二、填空题1..2.15．3.         4.25.．6.200．7.2508.1700．三、解答题1.(1)解：设经过x秒，甲乙两人首次相遇，依据题意得：8x＋6x＝400－8，解得：x＝28答：经过28秒甲乙两人首次相遇；(2)解：设经过y秒，甲乙两人首次相遇，依据题意得：8y－6y＝400－8，解得：y＝196，答：经过196秒两人首次相遇． 2.设走路快的人走了步追上走路慢的人，则根据题意可列方程如下：．解得：．（步）．答：走路快的人需要走3000步才能追上走路慢的人． 3.解：（1）设xh相遇．由题意得：72x+48x=240，解得x=2；（2）设yh相遇．由题意得：72y−48y=240，解得y=10；（3）设xh后两车相距120km，若相遇前，则72x−48x=240−120，解得x=5；若相遇后，则72x−48x=240+120，解得x=15；答：5小时或15小时后两车相距120km． 4.当时，客车与乙城的距离为千米；解：设当客车与出租车相距100千米时客车的行驶时间是t小时  a：当客车和出租车没有相遇时    解得：   b：当客车和出租车相遇后     解得：   当客车与出租车相距100千米时客车的行驶时间是小时或小时小王选择方案二能更快到达乙城解：设客车和出租车x小时相遇 ， 此时客车走的路程为350km，出租车的路程为450km丙城与M城之间的距离为90km  方案一：小王需要的时间是  方案二：小王需要的时间是 小王选择方案二能更快到达乙城． 5.（1）设两车经过x秒相遇，根据题意得：（10+30）x=1200解得：x=30．答：两车经过30秒相遇；（2）设两车从相遇到完全离开所需的时间为y秒，根据题意得：（10+30）y=4+20解得：y=0.6．答：两车从相遇到完全离开所需的时间为0.6秒；（3）设AB表示车长为4米的小轿车，其中点A表示车头，点B表示车尾，A'B'表示车长为20米的大货车，其中点A'表示车头，点B'表示车尾，则AB=4米，A'B'=20米，设BB'=a米．分两种情况：①车尾相遇前，如图1，则AB'=（4﹣a）米．小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时，AA'=4BB'，所以20+4﹣a=4a，解得：a，则AA'，故所求时间为：（10+30）（秒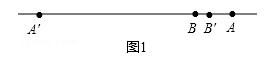）；②车尾相遇后，如图2，则AB'=（4+a）米．小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时，AA'=4BB'，所以20+4+a=4a，解得：a=8，则AA'=32，故所求时间为：32÷（10+30）（秒）．综上所述：当小轿车车头和大货车车头相遇后，小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间为秒或秒．