初中数学湘教版九年级上册5.1 总体平均数与方差的估计精品同步测试题

《5.1 总体平均数与方差的估计》课时同步练习2020-2021年数学湘教版九（上）

一．选择题（共10小题）

1．某同学现有一装有若干个黄球的袋子为了估计袋子中黄球的数量，该同学向这袋黄球中放入了40个绿球（所有球除颜色外其余均相同），摇匀后随机抓取60个，其中绿球共计10个，则袋子中黄球的数量约为（　　）

A．200个 B．220个 C．240个 D．280个

2．水产养殖中常采用“捉﹣﹣放﹣﹣捉”的方式估计一个鱼塘中鱼的数量，如从某个鱼塘中随机地捞出100条鱼，将这些鱼作上记号后再放回鱼塘，隔数日后再从该鱼塘随机捞出144条鱼，其中带有记号的有6条，从而估计该鱼塘有（　　）条鱼．

A．1600 B．2400 C．1800 D．2000

3．为了估计某地区梅花鹿的数量，先捕捉20只梅花鹿做上标记，然后放走，待有标记的梅花鹿完全混合于鹿群后，第二次捕捉100只梅花鹿，发现其中5只有标记．估计这个地区的梅花鹿的数量约有（　　）只．

A．200 B．300 C．400 D．500

4．某异地扶贫搬迁学生定点学校七年级共有1000人，为了了解这些学生的视力情况，从中抽查了20名学生的视力，对所得数据进行整理．若数据在4.8～5.1这一小组的频率为0.3，则可估计该校七年级学生视力在4.8～5.1范围内的人数有（　　）

A．600人 B．300人 C．150人 D．30人

5．一个口袋中装有n个红球和5个白球，它们除颜色外完全相同．在不允许将球倒出来的前提下，小明采取如下方法估计n的大小：从口袋中随机摸出一个球，记下颜色后再放回口袋中，摇匀后再随机摸出一球，记下颜色后再放回口袋中．不断重复上述过程，小明共摸了200次，其中50次摸到了白球，由此小明估计n的大小为（　　）

A．14 B．15 C．16 D．17

6．随机调查某小区10户家庭一周内使用环保方便袋的数量．得到数据如下（单位：只）：6，5，7，8，7，9，10，5，6，7，利用所得的数据估计该小区1500户家庭一周内需要环保方便袋约为（　　）

A．1500 B．10500 C．14000 D．15000

7．邵东市是全国重要的打火机生产基地．质检部门对市内某企业生产的A型打火机的质量进行抽样检测，随机抽查5盒（每盒30个打火机），5盒中合格打火机（单位：个）分别为26，29，29，30，27个，则估计某企业该型号的打火机的合格率为（　　）

A．92% B．94% C．96% D．98%

8．在一个不透明的袋子里，有若干完全相同的蓝色玻璃球，现将只有颜色不同的10个同款红色玻璃球放入袋中，充分混合后随机倒出20个，其中红色玻璃球有2个．由此可估计袋子里原有蓝色玻璃球大约（　　）

A．50个 B．80个 C．90个 D．100个

9．积极行动起来，共建节约型社会！我市某居民小区200户家庭参加了节水行动，现统计了10户家庭一个月的节水情况，将有关数据整理如下表：

请你估计该200户家庭这个月节约用水的总量是（　　）

A．100吨 B．180吨 C．200吨 D．250吨

10．在一个不透明的口袋中，装有若干个红球和3个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中红球的个数大约是（　　）

A．20个 B．16个 C．15个 D．12个

二．填空题（共6小题）

11．质检部门从2000件电子元件中随机抽取100件进行检测，其中有3件是次品．试据此估计这批电子元件中大约有　   　件次品．

12．为了解某区2400名初中教师中接种新冠疫苗的教师人数，随机调查了其中200名教师，结果有150人接种了疫苗，那么估计该区接种新冠疫苗的初中教师人数约有　     　人．

13．一个口袋中有若干个白球和8个黑球（除颜色外其余都相同），从口袋中随机摸出1球，记下其颜色，再把它放回，不断重复上述过程，共摸了200次，其中有57次摸到黑球，则据此估计口袋中大约有　   　个白球．

14．某县校服生产有甲、乙、丙三种方案，为了了解何种图案更受欢迎，随机调查了某校学生100名，其中有60位学生喜欢甲方案，若该校有学生3000名，根据你所学的统计知识，估计该校喜欢甲方案的学生有　     　人．

15．一个盒子中有5个红球和若干个白球，它们除颜色外都相同，从中随机摸出一个球，记下它的颜色后再放回盒子中．不断重复这个过程，共摸了100次球，发现有25次摸到红球，请估计盒子中白球大约有　   　个．

16．在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，则估计盒子中大约有红球　    　．

三．解答题（共4小题）

17．勤劳是中华民族的传统美德，学校要求学生在家帮助父母做一些力所能及的家务．在学期初，小丽同学随机调查了七年级部分同学寒假在家做家务的总时间，设被调查的每位同学寒假在家做家务的总时间为x小时，将做家务的总时间分为五个类别：A（0≤x＜10），B（10≤x＜20），C（20≤x＜30），D（30≤x＜40），E（x≥40）．并将调查结果绘制了如图两幅不完整的统计图：

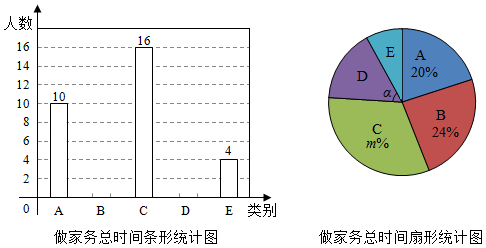
根据统计图提供的信息，解答下列问题：

（1）本次共调查了　   　名学生；

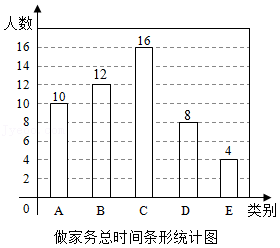
（2）根据以上信息直接在答题卡上补全条形统计图；

（3）扇形统计图中m＝　   　，类别D所对应的扇形圆心角α的度数是　   　度；

（4）若该校七年级共有400名学生，根据抽样调查的结果，估计该校七年级有多少名学生寒假在家做家务的总时间不低于20小时？

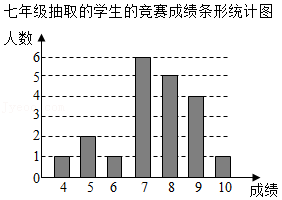
18．每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．

七、八年级抽取的学生的竞赛成绩统计表

根据以上信息，解答下列问题：

（1）填空：a＝　    　，b＝　    　，c＝　    　；

（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．

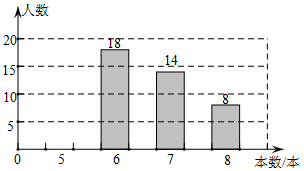
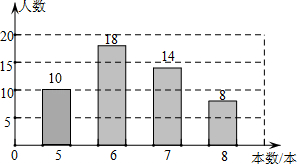
19．中央电视台的“朗读者”节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本书最少的有5本，最多的有8本，并根据调查结果绘制了不完整的图表，如图所示：

（1）统计表中的a＝　   　，b＝　   　，c＝　   　；

（2）请将条形统计图补充完整；

（3）求所有被调查学生课外阅读的平均本数；

（4）若该校八年级共有1200名学生，请你分析该校八年级学生课外阅读7本及以上的人数．

20．在对全市初中生进行的体质健康测试中，青少年体质研究中心随机抽取的10名学生的坐位体前屈的成绩（单位：厘米）如下：

11.2，10.5，11.4，10.2，11.4，11.4，11.2，9.5，12.0，10.2

（1）通过计算，样本数据（10名学生的成绩）的平均数是10.9，中位数是　     　，众数是　     　；

（2）一个学生的成绩是11.3厘米，你认为他的成绩如何？说明理由；

（3）研究中心确定了一个标准成绩，等于或大于这个成绩的学生该项素质被评定为“优秀”等级，如果全市有一半左右的学生能够达到“优秀”等级，你认为标准成绩定为多少？说明理由．

参考答案

一．选择题（共10小题）

1．解：袋子中求的总个数约为40÷＝240（个），

则黄球的个数为240﹣40＝200（个），

故选：A．

2．解：设鱼塘中有x条鱼，

根据题意，得：＝，

解得x＝2400，

经检验x＝2400是分式方程的解，

所以估计该鱼塘有2400条鱼，

故选：B．

3．解：设这个地区的梅花鹿的数量约有x只，

根据题意，得：＝，

解得x＝400，

经检验：x＝400是分式方程的解，

所以这个地区的梅花鹿的数量约400只，

故选：C．

4．解：估计该校七年级学生视力在4.8～5.1范围内的人数有1000×0.3＝300（人），

故选：B．

5．解：根据题意，得：＝，

解得n＝15，

经检验n＝15是分式方程的解，

故选：B．

6．解：∵小区10户家庭一周内使用环保方便袋的数量的平均数为＝7，

∴估计该小区1500户家庭一周内需要环保方便袋约为1500×7＝10500，

故选：B．

7．解：估计某企业该型号的打火机的合格率为×100%＝94%，

故选：B．

8．解：设袋子中蓝色玻璃球的个数为x，

根据题意，得：＝，

解得x＝90，

经检验x＝90是分式方程的解，

所以估计袋子中蓝色玻璃球的个数约为90个，

故选：C．

9．解：∵抽查的10户家庭这个月节约用水的平均数为＝1（吨），

∴估计该200户家庭这个月节约用水的总量是200×1＝200（吨），

故选：C．

10．解：设红球有x个，根据题意得，

3：（3+x）＝1：5，

解得x＝12，

经检验：x＝12是原分式方程的解，

所以估计盒子中红球的个数大约有12个，

故选：D．

二．填空题（共6小题）

11．解：估计这批电子元件中次品大约有2000×＝60（件），

故答案为：60．

12．解：估计该区接种新冠疫苗的初中教师人数约有2400×＝1800（人），

故答案为：1800．

13．解：设口袋中白球有x个，

根据题意，得：＝，

解得x≈20，

经检验x＝20是分式方程的解，

所以口袋中白球大约有20个，

故答案为：20．

14．解：估计该校喜欢甲方案的学生有3000×＝1800（人），

故答案为：1800．

15．解：设盒子中白球大约有x个，

根据题意，得：＝0.25，

解得x＝15，

经检验x＝15是分式方程的解，

所以估计盒子中白球大约有15个，

故答案为：15．

16．解：设盒子中有红球x个，

由题意可得：＝0.3，

解得：x＝14，

经检验，x＝14是分式方程的解．

故答案为14个．

三．解答题（共4小题）

17．解：（1）本次共调查了10÷20%＝50名学生，

故答案为：50；

（2）B类学生有：50×24%＝12（人），

D类学生有：50﹣10﹣12﹣16﹣4＝8（人），

补全的条形统计图如右图所示；

（3）m%＝16÷50×100%＝32%，

即m＝32，

类别D所对应的扇形圆心角α的度数是：360°×＝57.6°，

故答案为：32，57.6；

（4）400×＝224（人），

即该校七年级有224名学生寒假在家做家务的总时间不低于20小时．

18．解：（1）由图表可得：a＝＝7.5，b＝＝8，c＝8，

故答案为：7.5，8，8；

（2）该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数＝800×＝200（人），

答：该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数为200人；

（3）∵八年级的合格率高于七年级的合格率，

∴八年级“国家安全法”知识竞赛的学生成绩更优异．

19．解：（1）由题意c＝18÷0.36＝50，

∴a＝50×0.2＝10，b＝＝0.28，

故答案为10，0.28，50．

（2）条形统计图如图所示．

（3）所有被调查学生课外阅读的平均本数＝＝6.4（本）

（4）该校八年级共有1200名学生，该校八年级学生课外阅读7本及以上的人数有1200×＝528（名）．

20．解：（1）中位数是11.2，众数是11.4．

（2）方法1：根据（1）中得到的样本数据的结论，可以估计，在这次坐位体前屈的成绩测试中，全市大约有一半学生的成绩大于11.2厘米，有一半学生的成绩小于11.2厘米，这位学生的成绩是11.3厘米，大于中位数11.2厘米，可以推测他的成绩比一半以上学生的成绩好．

方法2：根据（1）中得到的样本数据的结论，可以估计，在这次坐位体前屈的成绩测试中，全市学生的平均成绩是10.9厘米，这位学生的成绩是11.3厘米，大于平均成绩10.9厘米，可以推测他的成绩比全市学生的平均成绩好．

（3）如果全市有一半左右的学生评定为“优秀”等级，标准成绩应定为11.2厘米（中位数）．因为从样本情况看，成绩在11.2厘米以上（含11.2厘米）的学生占总人数的一半左右．可以估计，如果标准成绩定为11.2厘米，全市将有一半左右的学生能够评定为“优秀”等级．