湘教版八年级上册2.4 线段的垂直平分线精品课后练习题

2.4　线段的垂直平分线

基础过关全练

知识点1　线段的垂直平分线

1.(2020湖南邵阳隆回期中)如图,P是线段AB的垂直平分线上的一个点,PA=6 cm,则线段PB的长为　(　　)

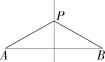
A.3 cm 　B.4 cm 　C.6 cm　 D.8 cm

2.(2022贵州贵阳期末)如图,在△ABC中,D是线段AB的垂直平分线上一点,∠CAD=80°,∠C=50°,则∠B的度数是(　　)

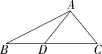
A.25°　 B.30° 　C.40° 　D.50°

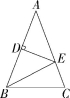
3.(2022湖南邵阳期中)如图,△ABC中,AB=AC,线段AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是

40 cm,24 cm,则AB=　　　　cm. 

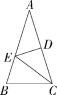
4.(2022湖南永州道县期中)如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.

(1)求∠ECD的度数;

(2)若CE=5,求BC的长.

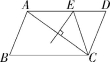
5.(2022独家原创)如图,四边形ABCD中,AC的垂直平分线交AD于E.

(1)若CD=3,AD=5,求△CDE的周长;

(2)若∠CAD=32°,∠D=64°,求证:CE=CD.

知识点2　线段垂直平分线的性质定理的逆定理

6.(2022湖南永州宁远期中)下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是(　　)

A.CA=CB,DA=DB

B.CA=CB,CD⊥AB

C.CA=DA,CB=DB

D.CA=CB,CD平分AB

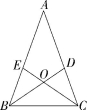
7.如图,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于点O.

求证:点O在线段BC的垂直平分线上.

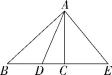
8.如图,在△ABC中,AD为∠BAC的平分线,以A为顶点,AC为一边在

△ABC外部作∠CAE=∠B,边AE交边BC的延长线于点E,求证:点E在线段AD的垂直平分线上.

知识点3　与线段垂直平分线有关的作图

9.如图,在△ABC中,∠B=68°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为(　　)

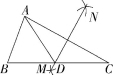
A.50° 　B.52°  　C.54°　  D.56°

能力提升全练

10.(2021广西梧州中考,6,)如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是(　　)

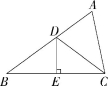
A.10.5　  B.12　   C.15　   D.18

11.(2020湖北宜昌中考,4,)如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(　　)

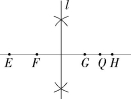
A.直线l是线段EH的垂直平分线

B.直线l是线段EQ的垂直平分线

C.直线l是线段FH的垂直平分线

D.EH是l的垂直平分线

12.(2020青海中考,5,)如图,△ABC中,AB=AC=14 cm,AB的垂直平分线MN交AC于点D,且△DBC的周长是24 cm,则BC=　　　　cm. 

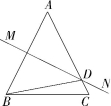
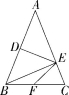
13.(2022湖南常德澧县期中,16,)如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,EF=BF,则∠EFC=　　　　°. 

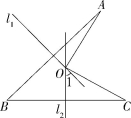
14.(2020江苏南京中考,15,)如图,线段AB、BC的垂直平分线l1、l2相交于点O.若∠1=39°,则∠AOC=　　　　°. 

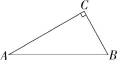
15.(2022湖南怀化溆浦期中,21,)如图,△ABC中,∠C=90°,

∠A=30°.

(1)用尺规作AB边上的中垂线DE,交AC于点D,交AB于点E;(保留作图痕迹,不要求写作法和证明)

(2)连接BD,求证:BD平分∠CBA.

素养探究全练

16.[逻辑推理](2022湖南通道期中)根据下列图形,解答问题:

(1)如图1,在△ABC中,AB=AC,∠BAC=100°,DE、FG分别是边AB、AC的垂直平分线,求∠DAG的度数;

(2)若去掉(1)中“AB=AC”的条件,其余条件不变(如图2),还能求出∠DAG的度数吗?若能,请求出∠DAG的度数;若不能,请说明理由;

(3)在(2)的情况下,试探索△ADG的周长与BC长的关系.

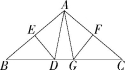
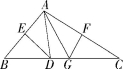
图1            图2

答案全解全析

基础过关全练

1.C　∵P是线段AB的垂直平分线上的点,PA=6 cm,∴PB=PA=6 cm.

2.A　∵∠CAD=80°,∠C=50°,∴∠ADC=50°,

∵D是线段AB的垂直平分线上一点,

∴AD=BD,∴∠B=∠BAD=∠ADC=25°.

3.16

解析　∵直线DE是线段AB的垂直平分线,

∴AE=BE.

∴△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,

∵△ABC的周长=AB+AC+BC,

∴△ABC的周长-△EBC的周长=AB,

∴AB=40-24=16 cm.

4.解析　(1)∵DE垂直平分AC,

∴CE=AE,∴∠ECD=∠A=36°.

(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,

由(1)知∠ECD=∠A=36°,

∴∠BEC=∠A+∠ECD=72°,

∴∠BEC=∠B,∴BC=CE=5.

5.解析　(1)∵AC的垂直平分线交AD于E,∴AE=CE,

∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=5+3=8.

(2)证明:∵∠CAD=32°,AE=CE,

∴∠ACE=∠CAD=32°,

∴∠DEC=∠ACE+∠CAD=32°+32°=64°,

∵∠D=64°,∴∠DEC=∠D,∴CE=CD.

6.C　当CA=DA,CB=DB时,直线CD不一定是线段AB的垂直平分线,故选C.

7.证明　∵AB=AC,∴∠ABC=∠ACB,

∵∠ABC,∠ACB的平分线BD,CE相交于点O,

∴∠DBC=∠ABC,∠BCE=∠ACB,∴∠DBC=∠BCE,∴BO=CO,

∴点O在线段BC的垂直平分线上.

8.证明　∵AD为∠BAC的平分线,∴∠BAD=∠DAC,

∵∠ADE=∠BAD+∠B,∠DAE=∠DAC+∠CAE,∠B=∠CAE,

∴∠ADE=∠DAE,∴AE=DE,∴点E在线段AD的垂直平分线上.

9.D　∵在△ABC中,∠B=68°,∠C=28°,

∴∠BAC=180°-∠B-∠C=84°,

由题意得,直线MN是线段AC的垂直平分线,

∴DA=DC,∴∠DAC=∠C=28°,

∴∠BAD=∠BAC-∠DAC=84°-28°=56°.

能力提升全练

10.C　∵DE是△ABC的边BC的垂直平分线,∴DB=DC,

∴△ACD的周长=AD+CD+AC=AD+BD+AC=AB+AC,

∵AB=9,AC=6,∴△ACD的周长=9+6=15.

11.A　如图,∵直线l为线段FG的垂直平分线,

∴FO=GO,直线l⊥FG,

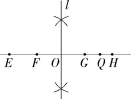
∵EF=GH,∴EF+FO=OG+GH,即EO=OH,

∴直线l为线段EH的垂直平分线,故选A.

12.10

解析　∵△DBC的周长是24 cm,

∴BD+DC+BC=24 cm,

∵MN垂直平分AB,∴AD=BD,

∴AD+DC+BC=24 cm,即AC+BC=24 cm,

又∵AC=14 cm,∴BC=24-14=10 cm.

13.45

解析　∵DE垂直平分AB,∴AE=BE,

∴∠A=∠ABE,

∵BE⊥AC,∴∠A=∠ABE=45°,

∵AB=AC,∴∠ABC=∠C==67.5°,

∴∠EBC=∠ABC-∠ABE=22.5°,

∵BF=EF,∴∠BEF=∠EBC=22.5°,

∴∠EFC=∠EBC+∠BEF=45°.

14.78

解析　如图,连接BO并延长,设l1交AB于点D,l2交BC于点E.

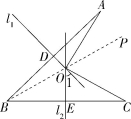
∵线段AB、BC的垂直平分线l1、l2相交于点O,

∴OA=OB=OC,∴∠A=∠OBA,∠C=∠OBC,

∴∠AOP=2∠ABO,∠COP=2∠CBO,

∴∠AOC=∠AOP+∠COP=2(∠ABO+∠CBO)=2∠ABC.

∵∠BDO=∠BEO=90°,

∴∠DOE+∠ABC=360°-∠BDO-∠BEO=180°,

∵∠DOE+∠1=180°,

∴∠ABC=∠1=39°,

∴∠AOC=2∠ABC=78°.

15.解析　(1)如图所示,DE就是要求作的AB边上的中垂线.

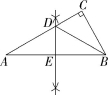
(2)证明:如图,∵DE是AB边上的中垂线,

∴AD=BD,∴∠ABD=∠A=30°,

∵∠C=90°,∴∠ABC=90°-∠A=90°-30°=60°,

∴∠CBD=∠ABC-∠ABD=60°-30°=30°,

∴∠ABD=∠CBD,∴BD平分∠CBA.

素养探究全练

16.解析　(1)∵DE垂直平分AB,

∴DA=DB,∴∠B=∠BAD,

∵GF垂直平分AC,∴GA=GC,∴∠C=∠GAC,

∵∠B+∠C+∠BAC=180°,∠BAC=100°,

∴∠B+∠C=80°,∴∠BAD+∠GAC=80°,

∴∠DAG=∠BAC-(∠BAD+∠GAC)=100°-80°=20°.

(2)能.

∵DE垂直平分AB,∴DA=DB,∴∠B=∠BAD,

∵GF垂直平分AC,∴GA=GC,∴∠C=∠GAC,

∵∠B+∠C+∠BAC=180°,∠BAC=100°,

∴∠B+∠C=80°,∴∠BAD+∠GAC=80°,

∴∠DAG=∠BAC-(∠BAD+∠GAC)=100°-80°=20°.

(3)由(2)知,AD=BD,AG=GC,

∴AD+DG+AG=BD+DG+GC=BC.

即△ADG的周长等于BC的长.