


湘教版八年级上册2.1 三角形优秀复习练习题
展开2.6 用尺规作三角形
基础过关全练
知识点1 作一个角的平分线
1.如图,已知∠AOB,求作射线OC,使OC平分∠AOB,那么作法的合理顺序是( )
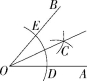
①作射线OC;
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于![]() DE的长为半径在∠AOB内作弧,两弧交于点C.
DE的长为半径在∠AOB内作弧,两弧交于点C.
A.①②③ B.②①③
C.②③① D.③①②
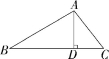
2.如图,在△ABC中,AD是△ABC的高,∠B=30°,∠C=52°.
(1)尺规作图:作△ABC的角平分线AE(只保留作图痕迹,不写作法);
(2)求∠DAE的大小.
知识点2 作一个角等于已知角
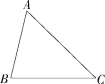
3.(2020陕西中考)如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹,不写作法)
知识点3 作三角形
4.尺规作图(只保留作图痕迹,不要求写出作法).
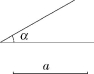
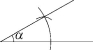
如图,已知∠α和线段a.
求作:△ABC,使∠A=∠α,∠C=90°,AB=a.
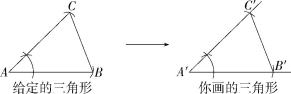
5.学过尺规作图后,就可以用尺规画出一个与已知三角形一模一样的三角形.比如给定△ABC(如图所示),可以这样来画:先作一条与AB相等的线段A'B',然后作∠B'A'C'=∠BAC,再作线段A'C'=AC,最后连接B'C',这样△A'B'C'就和已知的△ABC一模一样了.请你根据上面的作法画一个与给定的三角形一模一样的三角形.(请保留作图痕迹)
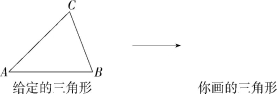
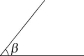
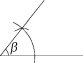
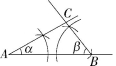
6.如图,已知∠α,∠β和线段c,用直尺和圆规作出△ABC,使∠A=
∠α,∠B=∠β,AB=c.(要求画出图形,并保留作图痕迹,不必写出作法)
![]()
![]()
能力提升全练
7.(2021吉林长春中考改编,7,![]() )在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
)在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
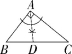
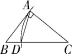
A B
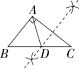
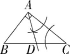
C D
8.(2020湖南娄底涟源期末,10,![]() )如图,在△ABC中,AC=BC,
)如图,在△ABC中,AC=BC,
∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
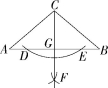
A.40° B.45° C.50° D.60°
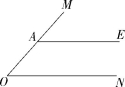
9.(2020湖南益阳安化马路镇中学期中,17,![]() )如图,A是∠MON的边OM上一点,AE∥ON.
)如图,A是∠MON的边OM上一点,AE∥ON.
(1)尺规作图:作∠MON的平分线OB,交AE于点B(保留作图痕迹,不写作法);
(2)若∠MAE=48°,直接写出∠OBE的度数.
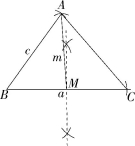
10.(2020湖南长沙一中岳麓中学月考,19,![]() )如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
)如图,已知线段a、c和m,求作:△ABC,使BC=a,AB=c,BC边上的中线AM=m.
要求:不写作法,保留作图痕迹,标注字母.

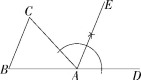
11.(2021广西河池中考,21,![]() )如图,∠CAD是△ABC的外角.
)如图,∠CAD是△ABC的外角.
(1)尺规作图:作∠CAD的平分线AE(不写作法,保留作图痕迹);
(2)若AE∥BC,求证:AB=AC.
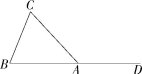
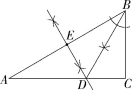
12.(2022湖南永州零陵期中,25,![]() )已知:如图,在△ABC中,∠A=
)已知:如图,在△ABC中,∠A=
30°,∠B=60°.
(1)作∠ABC的平分线BD,交AC于点D;作AB的中点E;(要求:尺规作图,保留作图痕迹,不必写作法和证明)
(2)连接DE,求证:△ADE≌△BDE.
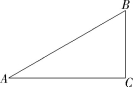
13.(2022湖南株洲攸县期中,21,![]() )如图,四边形ABCD中,AB∥CD,∠A=60°.
)如图,四边形ABCD中,AB∥CD,∠A=60°.
(1)作∠ADC的平分线DE,交AB于点E;(要求:尺规作图,保留作图痕迹,不必写作法和证明)
(2)判断△ADE是什么三角形,并说明理由.

素养探究全练
14.[直观想象](2021湖南长沙中考)人教版初中数学教科书八年级上册第35~36页告诉我们作一个三角形与已知三角形全等的方法:
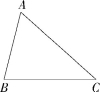
已知:△ABC.
求作:△A'B'C',使得△A'B'C'≌△ABC.
作法:如图.
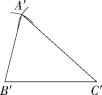
(1)画B'C'=BC;
(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';
(3)连接线段A'B',A'C',则△A'B'C'即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在△A'B'C'和△ABC中,
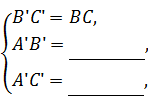
∴△A'B'C'≌ .
(2)这种作一个三角形与已知三角形全等的方法的依据是 .(填序号)
①AAS;②ASA;③SAS;④SSS.
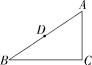
15.[逻辑推理]如图,在Rt△ABC中,∠C=90°,D是AB的中点,AC<BC.
(1)试用无刻度的直尺和圆规,在BC上作一点E,使得直线ED平分
△ABC的周长;(不要求写作法,但要保留作图痕迹)
(2)在(1)的条件下,若DE分直角△ABC的面积为1∶2两部分,请探究AC与BC的数量关系.
答案全解全析
基础过关全练
1.C 根据作一个角的平分线的过程可知,作法的合理顺序是②③①.
2.解析 (1)如图,AE为所求作的线段.
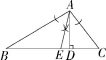
(2)∵∠B=30°,∠C=52°,
∴∠BAC=180°-∠B-∠C=98°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=49°,
∠BAC=49°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=38°,
∴∠DAE=∠EAC-∠DAC=49°-38°=11°.
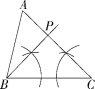
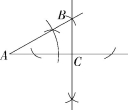
3.解析 如图,点P即为所求.
4.解析 如图,△ABC为所求作的图形.
5.解析 如图所示,△A'B'C'即为所求作的三角形.
6.解析 如图,△ABC即为所求作的三角形.
![]()
能力提升全练
7.A A.由作图可知AD是△ABC的角平分线,不能得出△ADC是等腰三角形;B.由作图可知CA=CD,故△ADC是等腰三角形;C.由作图可知DA=CD,故△ADC是等腰三角形;D.由作图可知DA=CD,故△ADC是等腰三角形.
8.C 观察题图中的作图痕迹可知CG⊥AB,又CA=CB,∴CF平分∠ACB,∠A=∠B=40°,∴∠BCG=90°-40°=50°.
9.解析 (1)如图,OB为所作.
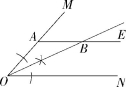
(2)∵AE∥ON,∴∠MON=∠MAE=48°,
∵OB平分∠MON,
∴∠NOB=![]() ∠MON=24°,
∠MON=24°,
∵AE∥ON,
∴∠OBE=180°-∠BON=180°-24°=156°.
10.解析 如图所示,△ABC是所求作的三角形.
11.解析 (1)如图,射线AE即为所求.
(2)证明:∵AE平分∠CAD,
∴∠EAD=∠EAC,
∵AE∥BC,
∴∠B=∠EAD,∠C=∠EAC,
∴∠B=∠C,∴AB=AC.
12.解析 (1)∠ABC的平分线BD,AB的中点E如图所示.
(2)证明:如图,∵BD平分∠ABC,
∴∠ABD=![]() ×60°=30°,∵∠A=30°,
×60°=30°,∵∠A=30°,
∴∠ABD=∠A,∴AD=BD,
在△ADE和△BDE中,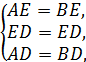
∴△ADE≌△BDE(SSS).
13.解析 (1)如图,射线DE即为所求.
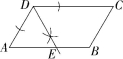
(2)△ADE是等边三角形.
理由:∵AB∥CD,∴∠CDE=∠AED,
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AD=AE,
∴△ADE是等腰三角形,
∵∠A=60°,
∴△ADE是等边三角形.
素养探究全练
14.解析 (1)AB;AC;△ABC. (2)④.
15.解析 (1)如图,直线DE即为所求.
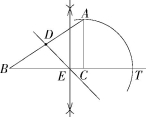
(2)∵DE分直角△ABC的面积为1∶2两部分,
∴BE=2EC,设EC=a,则BE=2a,
∴BC=3a,BE=ET=2a,
∴AC=ET-EC=a,
∴BC=3AC.
湘教版八年级上册2.6 用尺规作三角形课后复习题: 这是一份湘教版八年级上册2.6 用尺规作三角形课后复习题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
数学八年级上册2.6 用尺规作三角形一课一练: 这是一份数学八年级上册2.6 用尺规作三角形一课一练,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
湘教版第4章 一元一次不等式(组)4.1 不等式精品当堂检测题: 这是一份湘教版第4章 一元一次不等式(组)4.1 不等式精品当堂检测题,共7页。试卷主要包含了1 不等式,下列各式,下列各选项中,蕴含不等关系的是,下列表示的不等关系中,正确的是等内容,欢迎下载使用。













