初中数学湘教版八年级上册2.1 三角形精品巩固练习

第2章三角形单元复习习题精选

(满分100分,限时60分钟)

一、选择题(每小题3分,共30分)

1.(2022湖南株洲攸县期中)下列长度的三条线段不能组成三角形的是(　　)

A.5,5,10　B.4,5,6

C.4,4,4 　D.3,4,5

2.(2022独家原创)下列命题为假命题的是 (　　)

A.三边分别相等的两个三角形全等

B.有两边和一角分别相等的两个三角形全等

C.有一个角是60°的等腰三角形是等边三角形

D.面积相等的两个等腰直角三角形一定全等

3.(2022湖南邵阳期中)如图,△ABC≌△BAD,A和B,C和D是对应点.如果∠D=70°,∠CAB=50°,那么∠DAB的度数是(　　)

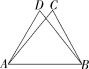
A.80°　B.70°　C.60°　D.50°

4.已知等腰三角形的周长为19,其中一边长为3,则该等腰三角形的底边长是(　　)

A.3　B.8　C.3或8　D.13

5.(2020山东枣庄中考)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为(　　)

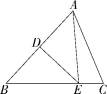
A.8　B.11　C.16　D.17

6.(2021江苏宿迁中考)如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是(　　)

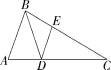
A.30°　B.40°　C.50°　D.60°

7.(2021湖南邵阳期中)如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于(　　)

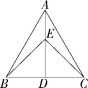
A.15°　B.30°　C.45°　D.60°

8.如图,一艘轮船由海平面上A地出发向南偏西40°的方向行驶100海里到达B地,再由B地向北偏西20°的方向行驶100海里到达C地,则A,C两地相距(　　)

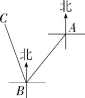
A.40海里　B.60海里

C.80海里　D.100海里

9.(2022湖南永州道县期中)如图,已知∠1=∠2,若利用“SAS”判定△ACB≌△BDA,还需添加的条件是(　　)

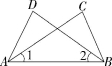
A.AD=BC　B.AC=BD

C.∠D=∠C　D.∠DAB=∠CBA

10.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,下列结论:①△BDF是等腰三角形;

②DE=BD+CE;③若∠A=50°,则∠BFC=105°;④BF=CF.其中正确的有(　　)

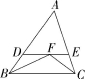
A.1个　B.2个　C.3个　D.4个

二、填空题(每小题3分,共18分)

11.(2022湖南张家界期中)如图,把手机放在一个支架上面,就可以非常方便地使用它上网课,这样做的数学道理是　　　　　　　　.

12.将命题“两个全等三角形的面积相等”写成“如果……,那么……”的形式为　　　　　　　　　　　　　　　　　　　. 

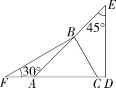
13.(2022北京海淀期中)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图是由一副三角尺拼凑得到的,图中∠ABC=　　　　. 

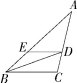
14.如图,在△ABC中,∠ABC的平分线交AC于点D,AD=6,过点D作DE∥BC交AB于点E,若△AED的周长为16,则边AB的长为　　　　. 

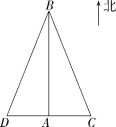
15.如图,两车从南北方向的路段AB的A端出发,分别向东、向西行驶相同的距离,到达C、D两地,此时可以判断C、D两地到B地的距离相等,其理由是　　　　　　　　　　　　　　　　　　　　　. 

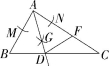
16.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,适当的长为半径作弧,交AB于点M,交AC于点N,分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为　　　　. 

三、解答题(共52分)

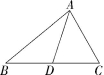
17.(8分)如图所示,已知AD是△ABC的边BC上的中线.

(1)作出△ABD的边BD上的高;

(2)若△ABC的面积为10,求△ADC的面积;

(3)若△ABD的面积为6,且BD边上的高为3,求BC的长.

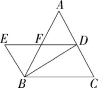
18.(8分)如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,

BE⊥BD,DE∥BC,DE交AB于点F.

(1)若∠A=56°,求∠E的度数;

(2)求证:BF=EF.

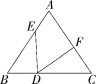
19.(2022湖南永州宁远期中)(10分)如图,在△ABC中,AB=AC,

BD=CF,BE=CD.

(1)求证:△BDE≌△CFD;

(2)若∠A=70°,求∠EDF的度数.

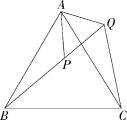
20.(2022湖南邵阳期中)(12分)如图,在等边三角形ABC中,点B、P、Q在同一条直线上,且∠ABP=∠ACQ,∠BAP=∠CAQ.

(1)判断△APQ是什么形状,并说明理由;

(2)求∠BQC的度数.

21.(2021湖南岳阳经开区期中)(14分)如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.

(1)试判断BD与AC的位置关系和数量关系,并说明理由;

(2)如图2,将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;

(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.

(i)试猜想BD与AC的数量关系,并说明理由;

(ii)你能求出BD与AC所夹锐角的度数吗?如果能,请直接写出所夹锐角的度数;如果不能,请说明理由.

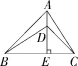
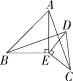
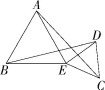
图1      图2        图3   

答案全解全析

1.A　5+5=10,不符合三角形的三边关系,不能组成三角形,故选A.

2.B　有两边和这两边的夹角分别相等的两个三角形全等,故选项B是假命题.

3.C　∵△ABC≌△BAD,A和B,C和D是对应点,

∴∠DBA=∠CAB=50°,

∴∠DAB=180°-∠D-∠DBA=180°-70°-50°=60°.

4.A　当3是腰长时,底边长为19-3×2=13,此时3+3=6<13,不能组成三角形;当3是底边长时,腰长为×(19-3)=8,此时3+8=11>8,能组成三角形.所以等腰三角形的底边长是3.故选A.

5.B　∵DE垂直平分AB,

∴AE=BE,

∴△ACE的周长=AE+CE+AC=BE+CE+AC=BC+AC=6+5=11.故选B.

6.B　∵∠A=70°,∠C=30°,

∴∠ABC=180°-∠A-∠C=80°,

∵BD平分∠ABC,

∴∠ABD=∠ABC=40°,

∵DE∥AB,

∴∠BDE=∠ABD=40°.

7.A　∵△ABC是等边三角形,

∴∠ABC=∠ACB=60°,

∵AD⊥BC,

∴BD=CD,AD所在直线是线段BC的垂直平分线,

∴BE=CE,

∴∠ECB=∠EBC=45°,

∴∠ACE=60°-45°=15°.

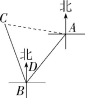
8.D　如图,连接AC.由题意得∠ABD=40°,∠CBD=20°,

∴∠CBA=∠ABD+∠CBD=60°.

又∵BC=BA,∴△ABC为等边三角形,

∴AC=BC=AB=100海里.

9.B　A.当添加条件AD=BC时,由已知条件无法判定△ACB≌△BDA;B.当添加条件AC=BD时,根据“SAS”可判定△ACB≌△BDA;C.当添加条件∠D=∠C时,根据“AAS”可判定△ACB≌△BDA;D.当添加条件∠DAB=∠CBA时,根据“ASA”可判定△ACB≌△BDA.故选B.

10.B　∵DE∥BC,∴∠DFB=∠FBC,

∵BF是∠ABC的平分线,

∴∠FBC=∠FBD,

∴∠DBF=∠DFB,

∴△BDF是等腰三角形,

故①中的结论正确;

同理可得△ECF是等腰三角形,

∴EF=CE,

由①知△BDF是等腰三角形,∴DF=DB,

∴DE=DF+FE=DB+CE,故②中的结论正确;

若∠A=50°,则∠BFC=180°-(∠FBC+∠FCB)=180°-(180°-∠A)=

90°+×50°=115°,故③中的结论错误;

△BDF,△ECF都是等腰三角形,但无法证全等,故④中的结论错误.

综上,正确的有2个.

11.三角形的稳定性

12.如果两个三角形全等,那么这两个三角形的面积相等

解析　命题的条件是“两个三角形全等”,结论是“这两个三角形的面积相等”.

13.75°

解析　∵∠F=30°,∠EAC=45°,

∴∠ABF=∠EAC-∠F=45°-30°=15°,

∵∠FBC=90°,

∴∠ABC=∠FBC-∠ABF=90°-15°=75°.

14.10

解析　∵BD平分∠ABC,

∴∠EBD=∠DBC,

∵DE∥BC,∴∠EDB=∠DBC,

∴∠EBD=∠EDB,

∴BE=ED,

∵△AED的周长为16,

∴AE+ED+DA=16,

∴AE+BE+6=16,

∴AE+BE=10,即AB=10.

15.线段垂直平分线上的点到线段两端的距离相等

解析　∵AB⊥CD,AC=AD,

∴AB所在直线垂直平分线段CD,

∴BC=BD,即C、D两地到B地的距离相等.

16.12

解析　∵AB=5,AC=8,AF=AB,

∴FC=AC-AF=AC-AB=8-5=3,

由作图方法可得AD平分∠BAC,

∴∠BAD=∠CAD,

在△ABD和△AFD中,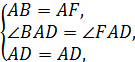

∴△ABD≌△AFD(SAS),

∴BD=DF,

∴△DFC的周长=DF+DC+FC=BD+DC+FC=BC+FC=9+3=12.

17.解析　(1)如图所示,AE为△ABD的边BD上的高.

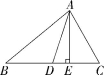
(2)∵AD是△ABC的边BC上的中线,△ABC的面积为10,

∴△ADC的面积=△ABC的面积=5.

(3)∵AD是△ABC的边BC上的中线,△ABD的面积为6,

∴△ABC的面积为12,

∵BD边上的高为3,

∴BC=12×2÷3=8.

18.解析　(1)∵AB=AC,∠A=56°,

∴∠ABC=∠ACB=×(180°-56°)=62°,

∵BD平分∠ABC,

∴∠DBF=∠DBC=∠ABC=31°,

∵DE∥BC,∴∠EDB=∠DBC=31°,

∵BE⊥BD,∴∠DBE=90°,

∴∠E=180°-90°-31°=59°.

(2)证明:∵BD平分∠ABC,

∴∠DBF=∠DBC,

∵DE∥BC,∴∠EDB=∠DBC,

∴∠EDB=∠FBD,

∵BE⊥BD,

∴∠EBF+∠DBF=∠E+∠BDE=90°,

∴∠E=∠EBF,

∴BF=EF.

19.解析　(1)证明:∵AB=AC,∴∠B=∠C,

在△BDE和△CFD中,

∴△BDE≌△CFD(SAS).

(2)∵∠A=70°,

∴∠B=∠C=×(180°-70°)=55°,

∴∠BED+∠BDE=180°-∠B=125°,

∵△BDE≌△CFD,

∴∠BED=∠CDF,

∴∠CDF+∠BDE=125°,

∴∠EDF=180°-125°=55°.

20.解析　(1)△APQ是等边三角形.

理由:∵△ACB是等边三角形,

∴AB=AC,∠BAC=60°,

在△ABP和△ACQ中,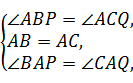

∴△ABP≌△ACQ(ASA),

∴AP=AQ,

∵∠BAP=∠CAQ,

∴∠BAP+∠PAC=∠PAC+∠CAQ,即∠BAC=∠PAQ=60°,

∴△APQ是等边三角形.

(2)如图,设BQ与AC交于O,

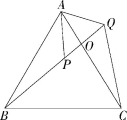
∵∠ABP=∠ACQ,∠AOB=∠QOC,

∴∠BQC=∠BAC=60°.

21.解析　(1)BD=AC,BD⊥AC.

理由:如图,延长BD交AC于F.

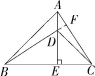
∵AE⊥BC,∴∠AEB=∠AEC=90°,

在△BED和△AEC中,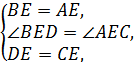

∴△BED≌△AEC,

∴BD=AC,∠DBE=∠CAE,

∵∠EBD+∠BDE=90°,∠BDE=∠ADF,

∴∠ADF+∠CAE=90°,

∴∠AFD=180°-90°=90°,

∴BD⊥AC.

(2)BD与AC的位置关系和数量关系都不发生变化.

理由:如图,设AC与BD的交点为F,AC与ED的交点为O,

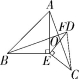
∵∠BEA=∠DEC=90°,

∴∠BEA+∠AED=∠DEC+∠AED,

即∠BED=∠AEC,

在△BED和△AEC中,

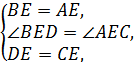
∴△BED≌△AEC(SAS),

∴BD=AC,∠BDE=∠ACE,

∵∠ACE+∠EOC=90°,∠EOC=∠DOF,

∴∠BDE+∠DOF=90°,

∴∠DFO=180°-90°=90°,

∴BD⊥AC.

∴BD与AC的位置关系和数量关系都不发生变化.

(3)(i)BD=AC.

理由:∵△ABE,△DCE为等边三角形,

∴∠BEA=∠DEC=60°,

∴∠BEA+∠AED=∠DEC+∠AED,

即∠BED=∠AEC,

在△BED和△AEC中,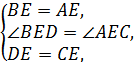

∴△BED≌△AEC(SAS),

∴BD=AC.

(ii)能.BD与AC所夹锐角的度数为60°.