


高中数学人教A版 (2019)必修 第一册3.4 函数的应用(一)优秀课后测评
展开![]() 函数的应用(一)
函数的应用(一)
一、图像判断类问题
例:
(1)下面是一幅统计图,根据此图得到的以下说法中,正确的个数是( )
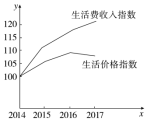 ①这几年生活水平逐年得到提高;
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1 B.2
C.3 D.4
(2)下列四个图象中,与所给三个事件吻合最好的顺序为( )
①我离开家不久,发现把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
②我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
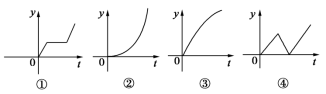
其中y表示离开家的距离,t表示所用时间.
A.④①② B.③①② C.②①④ D.③②①
(3)(多选题)某工厂八年来某种产品总产量![]() (即前
(即前![]() 年年产量之和)与时间
年年产量之和)与时间![]() (年)的函数关系如图,下列几种说法中正确的是( )
(年)的函数关系如图,下列几种说法中正确的是( )
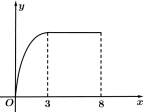
A.前三年中,总产量的增长速度越来越慢
B.前三年中,年产量的增长速度越来越慢
C.第三年后,这种产品停止生产
D.第三年后,年产量保持不变
二、一次、二次函数模型
例:
(4)下表是弹簧伸长长度![]() (单位:
(单位:![]() )与拉力
)与拉力![]() (单位:
(单位:![]() )的相关数据:
)的相关数据:
|
|
|
|
|
|
|
|
|
|
|
|
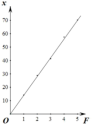
描点画出弹簧伸长长度随拉力变化的图像,并写出一个能基本反映这一变化现象的函数解析式.
(5)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
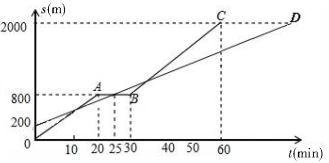
① 直接写出BC段图象所对应的函数关系式(不用写出t的取值范围)_______.
② 小明出发多长时间与爸爸第三次相遇?
③ 在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少多少分钟?
(6)已知某商品的进货成本为10(元/件),经过长时间调研,发现售价x(元)与月销售量y(件)满足函数关系式![]() .为了获得最大利润,商品售价应为( )
.为了获得最大利润,商品售价应为( )
A.80元 B.60元 C.50元 D.40元
(7)(多选题)某杂志以每册![]() 元的价格发行时,发行量为
元的价格发行时,发行量为![]() 万册.经过调查,若单册价格每提高
万册.经过调查,若单册价格每提高![]() 元,则发行量就减少
元,则发行量就减少![]() 册.要该杂志销售收入不少于
册.要该杂志销售收入不少于![]() 万元,每册杂志可以定价为( )
万元,每册杂志可以定价为( )
A.![]() 元 B.
元 B.![]() 元
元
C.![]() 元 D.
元 D.![]() 元
元
(8)如图是边长为100米的正方形场地,其中![]() 米,
米,![]() 米,
米,![]() 区域被占用,现在五边形
区域被占用,现在五边形![]() 区域内规划一个矩形
区域内规划一个矩形![]() 区域,使点P,M,N分别在线段
区域,使点P,M,N分别在线段![]() 上.
上.
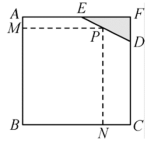 ① 设
① 设![]() 米,
米,![]() 米,将y表示成x的函数,求该函数的解析式及定义域;
米,将y表示成x的函数,求该函数的解析式及定义域;
② 求矩形![]() 面积的最大值,并确定点P的位置.
面积的最大值,并确定点P的位置.
(9)如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形![]() 的形状,它的下底
的形状,它的下底![]() 是圆
是圆![]() 的直径,上底
的直径,上底![]() 的端点在圆周上,设
的端点在圆周上,设![]() ,梯形
,梯形![]() 的周长为
的周长为![]() .
.
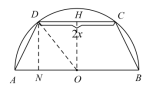
① 求出![]() 关于
关于![]() 的函数
的函数![]() 的解析式;
的解析式;
② 求![]() 的最大值,并指出相应的
的最大值,并指出相应的![]() 值.
值.
三、幂函数模型
例:
(10)美国对中国芯片的技术封锁激发了中国“芯”的研究热潮.某公司研发的![]() ,
,![]() 两种芯片都已经获得成功.该公司研发芯片已经耗费资金
两种芯片都已经获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产.经市场调查与预测,生产
千万元,现在准备投入资金进行生产.经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() ,其图像如图所示.
,其图像如图所示.
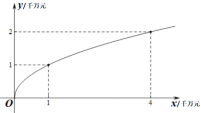
① 试分别求出生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式;
(千万元)的函数关系式;
② 现在公司准备投入![]() 0千万元资金同时生产
0千万元资金同时生产![]() ,
,![]() 两种芯片,求可以获得的最大利润是多少.
两种芯片,求可以获得的最大利润是多少.
(11)在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
① 写出函数解析式(可带参数);
② 假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的表达式;
四、分段函数模型
例:
(12)某公司生产某种电子产品的固定成本为2万元,每生产一台该产品需增加投入100元,已知总收入R(单位:元)与月产量x(单位:台)满足函数: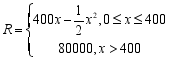
① 将利润![]() (单位:元)表示成月产量x的函数
(单位:元)表示成月产量x的函数
② 月产量x为何值时,公司所获利润最大,最大利润是多少?(利润+总成本=总收入)
(13)新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府![]() (万元)补贴后,防护服产量将增加到
(万元)补贴后,防护服产量将增加到![]() (万件),其中
(万件),其中![]() 为工厂工人的复工率(
为工厂工人的复工率(![]() ).A公司生产
).A公司生产![]() 万件防护服还需投入成本
万件防护服还需投入成本![]() (万元).
(万元).
① 将A公司生产防护服的利润![]() (万元)表示为补贴
(万元)表示为补贴![]() (万元)的函数;(政府补贴x万元计入公司收入)
(万元)的函数;(政府补贴x万元计入公司收入)
② 在复工率为k时,政府补贴多少万元才能使A公司的防护服利润达到最大?
③ 对任意的![]() (万元),当复工率
(万元),当复工率![]() 达到多少时,A公司才能不产生亏损?
达到多少时,A公司才能不产生亏损?
(精确到0.01).
(14)李庄村电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度每度0.5元,超过30度时,超过部分按每度0.6元.
方案二:不收管理费,每度0.58元.
① 求方案一收费![]() 元与用电量
元与用电量![]() (度)间的函数关系
(度)间的函数关系
② 李刚家月用电量在什么范围时,选择方案一比选择方案二更好?
(15)一家庭(父亲、母亲和孩子们)去某地旅游,甲旅行社说:“如果父亲买全票一张,其余 人可享受半票优惠.”乙旅行社说:“家庭旅行为集体票,按原价![]() 优惠.”这两家旅行社的原价是一样的.试就家庭里不同的孩子数,分别建立表达式,计算两家旅行社的收费,并讨论哪家旅行社更优惠.
优惠.”这两家旅行社的原价是一样的.试就家庭里不同的孩子数,分别建立表达式,计算两家旅行社的收费,并讨论哪家旅行社更优惠.
(16)某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:天)的关系符合图1中的折线表示的函数关系,西红柿种植成本
(单位:天)的关系符合图1中的折线表示的函数关系,西红柿种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:天)的关系符合图2中的抛物线表示的函数关系.
(单位:天)的关系符合图2中的抛物线表示的函数关系.
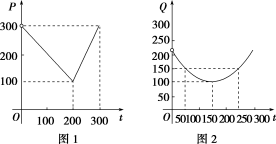
① 写出图1表示的市场售价与时间的函数关系式![]() ,图2表示的种植成本与时间的函数关系式
,图2表示的种植成本与时间的函数关系式![]() ;
;
② 若市场售价减去种植成本为纯收益,问何时上市的纯收益最大?
参考答案
(1)C
(2)A
(3)AC
(4)图见解析,![]() (F≥0).
(F≥0).
(5)(1) s=40t–400 (2) 37.5min (3) 3min
(6)D
(7)BC
(8)(1)![]() ,定义域为
,定义域为![]() ;(2)8000平方米;点P在点D的位置.
;(2)8000平方米;点P在点D的位置.
(9)(1)![]() ,
,![]() ;(2)
;(2)![]() 时,
时,![]() 的最大值是10.
的最大值是10.
(10)(1)生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式分别为
(千万元)的函数关系式分别为![]() ,
,![]()
![]() ,(2)9千万元
,(2)9千万元
(11)(1)![]() ;(2)
;(2)![]() .
.
(12)(1)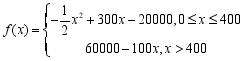 ;
;
(2)当月产量为300台时,公司所获利润最大,最大利润是25000.
(13)(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)0.65.
;(3)0.65.
(14)(1)![]() ;(2)25度到50度范围内(不含25、50度)时,选择方案一比方案二更好.
;(2)25度到50度范围内(不含25、50度)时,选择方案一比方案二更好.
(15)当家庭中只有一个孩子时,两家旅行社收费相等;当家庭中有两个以上孩子时,甲旅行社更优惠.
(16)(1)![]() ,
,![]() ,
,![]() ;(2)从2月1日开始的第
;(2)从2月1日开始的第![]() 天上市的西红柿的纯收益最大.
天上市的西红柿的纯收益最大.
数学必修 第一册3.4 函数的应用(一)随堂练习题: 这是一份数学必修 第一册<a href="/sx/tb_c4000270_t7/?tag_id=28" target="_blank">3.4 函数的应用(一)随堂练习题</a>,共10页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
高中数学4.5 函数的应用(二)同步练习题: 这是一份高中数学4.5 函数的应用(二)同步练习题,共9页。
人教A版 (2019)必修 第一册3.4 函数的应用(一)同步测试题: 这是一份人教A版 (2019)必修 第一册3.4 函数的应用(一)同步测试题,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













