数学必修 第一册3.1 函数的概念及其表示优秀教学设计

3.1函数的概念及其表示（第三课时）教学设计

一、内容及内容解析

（一）教学内容

1.函数的表示法；

2.分段函数。

（二）教学内容解析

学生在初中阶段已经接触了函数的三种表示，本节课直接给出函数的三种表示方法，并通过典型例题训练学生选择适当的方法表示函数，并且通过例题引进分段函数。学习函数的表示，不仅是研究函数本身和应用函数模型解决实际问题的需要，而且是进一步理解函数概念，深化对具体函数模型的认识需要。同时，基于高中所涉及的函数大多数均可用几种不同的方式表示，因此学习函数的表示也是向学生渗透数形结合的思想，培养学生直观想象素养的重要过程。

（三）教学重点

函数的三种表示法及各自的优缺点，分段函数。

二、教学目标

1.通过研究实例，能总结出函数三种表示法各自的特点，体会数形结合的思想．

2.通过用图象法表示一些函数，能利用函数图象探索解决问题的思路，体会利用图象简化代数运算的过程．

3.通过具体实例，能认识分段函数，并能简单应用．

三、教学问题诊断分析

问题：提炼函数的三种表示法各自的优缺点。

突破：课本3.1.1中四个实例为学习函数的三种表示方法做了铺垫。在实际教学中，先引导学生比较三种表示方法各自的特点，再师生一起进行评价并总结。

四、教学支持条件

为了增加学生对分段函数的理解，可以利用GGB软件，作出图像，让学生观察各段图象函数解析式.

五、教学过程设计

上一节我们已经学习过了函数的概念，那么函数的具体表示方法有哪些呢，在不同的情境中函数如何表示呢？带着这样的疑问来深入学习一下本节课的内容吧.

问题1：我们在初中已经接触过函数的三种表示法，分别是什么？如何表示？

师生活动：教师提出问题，学生观察思考后回答问题.根据学生的回答，教师进行必要的补充.

解析法，就是用数学表达式表示两个变量之间的对应关系.

列表法，就是列出表格来表示两个变量之间的对应关系.

图象法，就是用图象表示两个变量之间的对应关系.

设计意图：本节课就是学习函数的三种表示方法，通过回顾初中函数表示的三种方法，为后面的学习奠定基础。

问题2：你能根据所学知识，用三种表示法表示下面的例子？你能进一步总结函数三种表示法各自的优缺点吗？

例4某种笔记本的单价是5元，买个笔记本需要y元，试用函数的三种表示法表示函数.

师生活动：（1）学生思考后详细写出解题过程并展示.教师根据学生的答案进行评价纠错。

解：这个函数的定义域是数集.

用解析法可将函数表示为，.

用列表法可将函数表示为

用图象法可将函数表示为下图.

（2）追问1：比较函数的三种表示法，它们各自的特点是什么？

师生活动：学生口答，互相补充，教师总结提炼.

（3）追问2：所有函数都能用解析法表示吗？列表法与图象法呢？请你举出实例加以说明.

这个问题，学生比较难回答，教师先举一些例子（如习题3.1中的第17题）启发学生，再由学生试着举一些例子。

设计意图：学生通过具体例子理解函数的三种表示方法的特点及优缺点。

问题3：判断一个图形是不是函数图象的依据是什么？

师生活动：教师提出问题，学生分组讨论后回答问题.根据学生的回答，教师进行必要的补充.归纳：若垂直于x轴的直线与图像至多有一个交点，则这个图像可以作为某个函数的图像。

设计意图：使学生进一步理解函数的概念。

问题4：画出函数的图象吗？

师生活动：学生思考后详细写出解题过程并展示.教师根据学生的答案进行评价纠错。

解：由绝对值的概念，我们有.所以，函数的图象如图所示.

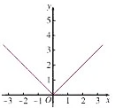
归纳：像例题中这样的函数称为分段函数，生活中，有很多可以用分段函数描述的实际问题.如出租车的计费、个人所得税纳税额等.

设计意图：让学生通过函数的不同表示，加强数形结合观念，培养学生直观想象能力。

问题5：你能根据所学，解决以下问题吗？

例6  给定函数,

(1)  在同一直角坐标系中画出函数的图像；

(2)  用表示中的较大者，记为

例如，当时，

请分别用图像法和解析法表示函数

师生活动：教师提出问题，学生分组讨论后回答问题.教学过程中，可以引导学生从纯代数运算的角度寻求函数的解析式表示。

设计意图：进一步加强学生数形结合观念和直观想象能力。

问题6：请同学们总结一下，本节课我们学习了哪些知识，掌握了哪些方法？

师生活动：老师可以提问同学作答，本节课学习了函数表示方法及分段函数。

设计意图：通过回顾本节课内容，形成知识体系，进行知识内化。

六、目标检测设计

课堂检测

1．购买某种饮料x听，所需钱数为y元，若每听2元，用解析法将y表示成x(x∈{1,2,3,4})的函数为(　　)

A．y＝2x　　　　　　　　　B．y＝2x(x∈R)

C．y＝2x(x∈{1,2,3，…})  D．y＝2x(x∈{1,2,3,4})

2.已知函数f(x)由下表给出，则f(f(3))等于（ ）

A．1      B.2         C．3       D．4

3.设函数，则=（   ）

A.       B.4    C.3    D. -3

4.已知函数f(x)是一次函数，若，则f(x)＝________；

5.已知f(x2＋2)＝x4＋4x2，则f(x)的解析式为________；

6.已知f(x)是一次函数，且f(f(x))＝4x－1，则f(x)＝________.

课后作业

教科书第69页练习1,2,3.

设计意图：巩固本节课的主要知识、方法.