

人教A版 (2019)必修 第一册4.3 对数优秀教案设计
展开(一)教学内容:对数的运算性质
(二)教学目标
1.通过对数式与指数式的互换发现并证明相应的对数运算性质,能利用对数运算性质简化运算,发展学生的逻辑推理和数学运算的核心素养.
2.通过感受换底公式的推导过程,体会换底公式的应用价值,感受对数运算的意义,发展学生的逻辑推理和数学运算的核心素养.
(三)教学重点及难点
1.重点
对数运算性质和换底公式
2.难点
对数运算性质和换底公式的推导
(四)教学过程
问题1:已知![]()
师生活动:教师强调题干信息,利用指数幂运算性质,让学生把对数化成指数,![]() ,得出
,得出![]() ,教师可以引导学生
,教师可以引导学生![]() ,则
,则![]() 可以写成
可以写成![]() .
.
设计意图:通过具体问题引出对数运算,激发学生探究欲望.
问题2:![]() ,可以推广
,可以推广![]()
师生活动(1):教师引导学生类比问题1,可令![]() ,因为
,因为![]()
则![]()
追问:仿照上述过程能证明![]() 吗?
吗?
师生活动:(2)学生类比上述问题自行证明,教师点评.
设计意图:利用好指对互换,推导对数运算性质1,加深学生理解对数概念的运算表达式.
问题3:可以利用上述性质1证明![]() 吗?
吗?
师生活动(1):教师引导移项证明![]() ,也引导学生仿照问题2利用指数幂运算证明,并指出我们把该性质作为对数运算性质2.
,也引导学生仿照问题2利用指数幂运算证明,并指出我们把该性质作为对数运算性质2.
追问:可以仿照![]() 推导
推导![]()
师生活动(2):让学生自己推导,教师点评,也可以引导学生当![]() 利用上述性质1理解该性质,并指出我们把该性质作为对数运算性质3.
利用上述性质1理解该性质,并指出我们把该性质作为对数运算性质3.
设计意图:通过类比问题2的推导方法,推导性质2,3强化学生运算技能,发展学生的逻辑推理素养.
问题4:根据上述对数运算性质完成下列问题吗?
(1)求下列各式的值:①![]() ;②
;②![]()
师生活动①:教师利用对数运算性质示范①,让学生自己尝试②
(2)用![]()
师生活动②:学生独立完成,教师进行指导.总结运用了上述哪些运算性质.
设计意图:(1)中直接运用对数的运算性质进行具体数值的计算,让学生体会对数运算把乘方转化为乘法,把乘法转换为加法的作用.(2)是关于字母的对数运算,强化对数运算性质的综合应用.
问题5利用计算工具求出![]() ,你能猜想他们三者之间的关系吗?
,你能猜想他们三者之间的关系吗?
师生活动:让学生通过手中的计算器计算,通过观察猜想出![]() .
.
师生活动:教师引导学生利用定义推导出换底公式![]()
教师可以示范从左边推出右边,可让学生尝试从右边推出左边.
设计意图:加强学生从定义、基本原理出发思考问题的意识,从解决具体问题的过程中启发并推导
出换底公式,培养学生从特殊到一般的思考意识和方法.
问题6:你能证明下面问题吗?
(1)证明:①![]() ②
②![]()
师生活动①:证明①教师提示学生使用换底公式,让学生自行证明,教师点评,证明②提示学生用换底公式以及对数运算性质3去尝试证明,分组尝试从左到右和从右到左的证明,j教师也可通过此题拓展换底
公式推论.
(2)尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量E(单位:焦耳)与地震里氏震级M之间的关系为![]() .2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
.2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
师生活动:教生共同分析,根据已知条件通过地震的里氏震级很容易求出![]() ,引导学生分析如何求能量比更方便.
,引导学生分析如何求能量比更方便.
教师示范具体解题过程:
解:设里氏9.0及和8.0级地震的能量分别为![]() .
.
由![]() ,可得
,可得![]() ,
,![]()
于是![]() .利用计算公就可得,
.利用计算公就可得,![]() .
.
得出结论地震级数仅相差一级,但释放出来的能量却是32倍.
设计意图:通过例题(1)让学生体会换底公式在运算中的妙处,强化对数运算能力,进一步感受对数运算的意义.例题(2)让学生明白在指数幂运算中,“指数增长”的变化非常快;在对数运算中,“对数增长”的变化就比较慢,也为后续函数模型应用的学习埋下伏笔.
(五)课堂小结
问题7:请同学们带着下列问题回顾本节课的学习内容,并给出回答
(1)对数与指数幂中指数是什么关系?
(2)对比指数运算性质与对数运算性质,结构上有何异同?
(3)换底公式在运算上的价值是什么?
师生活动: 先由学生独立思考、作答,再进行全班交流,教师和学生互动、点评后进行总结。
(1)对数与指数幂中指数的一种等价表示形式,我们要用好这一等价关系,通过指数运算性质得出相应的对数运算性质.
(2)同底指数幂相乘,底数不变指数相加,同底对数相加,底数不变真数相乘,同底指数幂相除,底数不变指数相减,同底对数相减,底数不变真数相除,我们在运算中要牢记性质,不要错用。
(3)有了换底公式,在没有计算工具时,通过查询常用对数表和自然对数表,计算出对数的值,也可通过换底化简运算等。
设计意图:进一步认识对数运算的研究内容、过程和方法,突出对数与指数运算的内在联系,渗透等价转化的思想方法。
(六)目标检测设计
课堂检测:
- 求出下列各式的值:
(1) ![]() (2)
(2)![]() (3)
(3)![]()
- 用
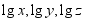 表示下列各式:
表示下列各式:
(1)![]() (2)
(2)![]()
- 化简下列各式:
(1)![]() (2)
(2)![]()
设计意图:检测对数运算性质及换底公式的掌握情况。
课后作业:
人教A版教材127页3,4,5,6,8题
设计意图:巩固对数的运算
(七)教学反思
高中数学4.3 对数表格教学设计: 这是一份高中数学4.3 对数表格教学设计,共3页。
高中数学人教A版 (2019)必修 第一册4.3 对数公开课教案及反思: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数公开课教案及反思,共2页。教案主要包含了内容和内容解析,目标及其解析,教学问题诊断分析,教学支持条件分析,课时分配设计等内容,欢迎下载使用。
【小单元教案】高中数学人教A版(2019)必修第一册--3.1.1 函数的概念(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--3.1.1 函数的概念(课时教学设计),共8页。













