

- 【小单元教案】高中数学人教A版(2019)必修第一册--4.4.3 不同函数增长的差异(课时教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--4.5 函数的应用(二)(单元教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--4.5.2 用二分法求方程的近似解(课时教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--4.5.3 函数模型的应用(第一课时)(课时教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--4.5.3 函数模型的应用(第二课时)(课时教学设计) 教案 2 次下载
【小单元教案】高中数学人教A版(2019)必修第一册--4.5.1 函数的零点与方程的解(课时教学设计)
展开![]() 第一课时 函数的零点与方程的解
第一课时 函数的零点与方程的解
(一)教学内容:函数零点的概念、函数零点存在定理
(二)教学目标
1.通过类比二次函数的零点的研究方法导出函数的零点的概念 ,能够数学地认识函数与方程的关系,形成将方程问题转化为函数问题、利用函数性质解决数学问题的习惯,发展学生数学抽象的数学核心素养;
2.通过观察对应二次函数在区间端点上的函数值的特征,能够导出函数零点存在定理,发展学生数形结合、将形转化为数的能力,发展学生数学抽象素养;
3.通过运算具体函数值的过程,感受指定区间内函数值的变化规律,寻找函数零点所在的区间,能够利用信息技术画出图象操作确认,尝试或转化的方法探索方程的有解区间,强化学生估算意识,培养近似计算的习惯,发展数学运算素养.
(三)教学重点及难点
1. 重点:函数零点的概念、函数零点存在定理
2. 难点:数学方式发现函数零点存在定理的理性思维方法
(四)教学过程设计
引导语 在“函数的应用(一)”的学习中,通过一些实例,我们已初步了解了建立函数模型解决实际问题的过程,学习了用函数描述客观事物变化规律的方法,本单元将继续学习运用函数性质求方程近似解的基本方法(二分法),再结合实例,更深入地理解用函数构建数学模型的基本过程,学习运用模型思想发现和提出问题、分析和解决问题的方法,今天我们先类比二次函数零点的研究方法一起探究:形如“lnx+2x-6=0”的不能用公式求解的方程解的情况,大家思考以下问题:
问题1:类比二次函数的零点的研究方法,怎样从函数的观点导出函数零点的概念?
师生活动:教师安排学生阅读教科书第147页阅读与思考“中外历史上的方程求解”后,类比二次函数的零点的概念的研究方法,由学生自主画出二次函数的图象,并观察此图象函数值的变化规律,尝试说出一般函数零点概念?
追问:你能再举出几个例子说明函数的零点、方程的解、图象与x轴的公共点的关系吗?并用函数的图象和性质找出零点及方程的解?
学生举例、画图、观察熟悉的函数图象,体会函数零点、方程的解、图象与x轴的公共点之间的关系,深入理解函数零点的概念的内涵.
 设计意图:安排学生完成阅读与思考“中外历史上的方程求解”,从高次代数方程解的探索历程,引导学生感受数学文化、体会逻辑的严谨性,理性认识函数与方程的关系,形成将方程的问题转化成函数问题、再利用函数性质解决问题的思维习惯,从具体例子出发,利用从具体到抽象的方法,导出一般函数零点的概念并得到相应的结论,发展学生的数学抽象素养.
设计意图:安排学生完成阅读与思考“中外历史上的方程求解”,从高次代数方程解的探索历程,引导学生感受数学文化、体会逻辑的严谨性,理性认识函数与方程的关系,形成将方程的问题转化成函数问题、再利用函数性质解决问题的思维习惯,从具体例子出发,利用从具体到抽象的方法,导出一般函数零点的概念并得到相应的结论,发展学生的数学抽象素养.
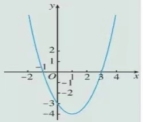
问题2:观察,如图,二次函数![]() 的图象,发现函数在区间[2,4]上有零点,此时函数图象与x轴有什么关系?
的图象,发现函数在区间[2,4]上有零点,此时函数图象与x轴有什么关系?
师生活动:教师提出问题,学生观察函数在给定区间内的图象部分与x轴有交点,体会此区间内自变量确定的函数值的变化特征,请说出函数的零点两侧函数值的变化情况.
追问1:计算![]() 在区间[-2,4]上是否也有这种特点?
在区间[-2,4]上是否也有这种特点?
学生运算函数![]() 得出
得出![]() ,在区间[-2,4]上不满足
,在区间[-2,4]上不满足![]() ,但函数存在零点,这一现象引发学生深入思考.
,但函数存在零点,这一现象引发学生深入思考.
追问2:你能举出几个例子并画出函数的图象,观察函数零点所在的区间,并计算在区间端点的函数值的积,是否有同样的结论吗?
学生通过举例画图分析,函数零点所在区间的特征,能够得出若有区间端点的函数值乘积为负,此区间内一定存在零点,反之,不一定成立.
设计意图:观察“函数图象与x轴的关系”的角度,与x轴公共点(3,0),且“穿过”x轴,在“图象连续不断”的条件下,把这两点结合起来,那么在零点所在区间内,零点的两边函数值一定异号.理解“图象穿过x轴”(形)用“函数的取值规律”(数)来表示,在“x=3的两侧函数值异号”,可以取端点为代表,即![]() .
.
追问3:请继续思考自己举出的函数例子,结合图象分析零点存在的条件,在此基础上归纳出零点存在的共同特征,能否概括出表达函数存在零点一个的命题?
学生分析举例存在零点的图象特征,归纳函数零点存在的结论,师生共完善,学生写在纸上,投影展示成果,再安排学生阅读教材第143页,“函数零点存在定理”的精准表达,学生思考,引导学生思辨其中关键语句的含义.
追问4:你怎样理解定理中的两个条件“在给定区间![]() 上连续”和“
上连续”和“![]() ”?思考定理的用处是什么?
”?思考定理的用处是什么?
学生举反例说明函数在给定区间内连续,结合图象得出如果区间端点乘积为负,则函数在此区间上至少有一个零点,师生总结得出:零点存在定理为研究方程的解提供了理论依据.
设计意图:按“导出定理---了解定理---应用定理”途径展开定理的研究,从逻辑的角度对定理中两个条件的充分性、必要性的考察,发展学生的数学抽象的数学学科素养.
问题3:你能说出求方程lnx+2x-6=0的实数解的个数研究方法吗?
 师生活动:教师提出不能用公式解决的方程解的问题,学生可能回答:计算机软件画图,根据图象直接判断;取特殊值估计解的情况;转化为两个函数后,画图由交点个数确定;用零点存在定理进行判断.按学生的想法进行尝试操作:
师生活动:教师提出不能用公式解决的方程解的问题,学生可能回答:计算机软件画图,根据图象直接判断;取特殊值估计解的情况;转化为两个函数后,画图由交点个数确定;用零点存在定理进行判断.按学生的想法进行尝试操作:
方法一:GGB画图可得方程解的个数,如图
方法二:考察函数![]() 的单调性
的单调性
![]()
![]() ,
,![]() ,
,![]() ,由函数的零点存在定理可知
,由函数的零点存在定理可知
函数![]() 存在零点
存在零点
![]() ,又因为函数
,又因为函数![]() 为单调增函数所以,方程lnx+2x-6=0有一个实数解;
为单调增函数所以,方程lnx+2x-6=0有一个实数解;
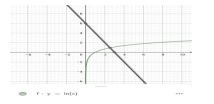
方法三:方程lnx+2x-6=0可转化为lnx=6-2x,同一平面直角坐标系
上画出两个基本初等函数图象,由交点情况,判断方程解的个数问题
方法四:借助计算工具化出画出函数y=lnx+2x-6的图象或列出x,y的对应值表,如下表格,并画出图象

由以上表格和图象可知,![]() ,
,![]() ,由零点存在定理可知函数
,由零点存在定理可知函数![]() ,可以用单调性定义容易证明函数
,可以用单调性定义容易证明函数![]() 是增函数,所以它只有一个零点,即相应方程lnx+2x-6=0只有一个解.
是增函数,所以它只有一个零点,即相应方程lnx+2x-6=0只有一个解.
追问1:为什么由图4.5-2和![]() 还不能说明函数
还不能说明函数![]() 只有一个零点?请举例说明;
只有一个零点?请举例说明;
学生举例说明对于给定区间上的函数,如,“连续不异号”“异号不连续”“不连续不异号”等都不能断定该函数是否存在零点;学生能够说出研究函数在某个区间上存在零点时,可借助函数的单调性来判断是否只有一个零点解决问题的方法.
追问2:你能证明函数![]() 是增函数吗?
是增函数吗?
学生能够给出两种思路:
方法一:函数![]() 单调性的证明思路,
单调性的证明思路,
类似方法二进行证明,可将其转化为两个基本函数的单调性的判断,令函数
![]() ,从而判断出函数
,从而判断出函数![]() ,
,
方法二:用单调函数定义进行增函数的证明,略
设计意图:通过追问,让学生得出“函数在单调区间上最多有一个零点”的结论,进一步得到方程解的个数问题的转化方法,在后继学习中经常用到,有助于提升学生的数学抽象素养;探究解法的多样性,培养学生多角度思考问题的习惯,发展学生高阶思维及数学运算素养.
(5) 课堂小结
问题4:通过本节课函数零点概念及函数零点存在定理的学习,联系函数与方程的研究内容及方法,你能说出求方程近似值的一般路径吗?
本节研究了函数的零点与方程的解、函数的零点存在定理,利用定理建立求方程近似解的一般步骤,学生经历从“情境+问题”思维过程,抽象出一般规律和结构,使其学会以简驭繁,养成一般性的思考问题的习惯;研究路径:“概念—定理一应用”,有利于学生形成系统性、普适性的数学思维模式.
问题5:在解决问题时,用到了哪些数学思想?
本节课在函数的零点与方程的解的转换过程中,逐步渗透了化归与转化思想、函数与方程思想和数形结合思想,发展了直观想象、数学抽象、数学运算、数学建模等数学核心素养.
(6) 目标检测设计
必做题:
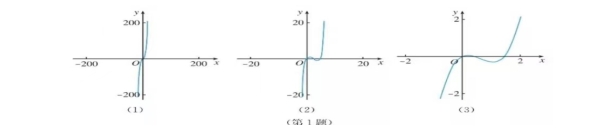 1.如图(1)(2)(3)分别为函数
1.如图(1)(2)(3)分别为函数![]() 在三个不同范围的图象,能否仅根据其中一个图象,得出函数
在三个不同范围的图象,能否仅根据其中一个图象,得出函数![]() 在某个区间只有一个零点的判断?为什么?
在某个区间只有一个零点的判断?为什么?
设计意图:本题通过函数图象加深对函数性质的深层理解,主要考查零点存在定理及单调性,观察不同函数区间的图象特征,加深理解函数存在零点理论,提升数形结合能力,发展学生数学抽象素养、直观想象等素养.
2.利用计算工具画出函数的图象,并指出下列函数零点所在的大致区间:
(1)![]() (2)
(2)![]()
(2)![]() (4)
(4)![]()
设计意图:通过信息技术绘制图象,能加深学生对零点存在定理的认识,对具体函数图象的实践操作,进一步理解数对形的定性刻画,对定理中的两个条件有了更深刻的思考,提升学生数形结合能力,发展直观想象素养.
3.已知函数![]() 的图象是一条连续不断的曲线,且有如下对应值表:
的图象是一条连续不断的曲线,且有如下对应值表:
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 136.136 | 15.552 | -3.92 | 10.88 | -52.488 | -232.064 |
函数![]() 在哪几个区间内一定有零点?为什么?
在哪几个区间内一定有零点?为什么?
设计意图:通过对表格中的数据理解,由已知点的坐标确定了的图象的特征及变化规律,为零点存在定理的应用提供了数与形的实证依据,提升了数学抽象素养、逻辑推理素养.
4.已知函数![]() ,求证:方程
,求证:方程![]() 在(-1,2)内至少有两个实数解.
在(-1,2)内至少有两个实数解.
设计意图:本题蕴含的转化思想,为学生提供了解决问题的一般方法,![]() 的实数解的问题可以转化为研究新函数
的实数解的问题可以转化为研究新函数![]() 的解的问题,先作出函数
的解的问题,先作出函数![]()
的图象,由图象的特征确定函数![]() 的零点情况,为函数的零点存在定理的使用提供了载体,在解决问题的过程中,发展了学生的数学抽象、数学运算、数学模型等数学核心素养.
的零点情况,为函数的零点存在定理的使用提供了载体,在解决问题的过程中,发展了学生的数学抽象、数学运算、数学模型等数学核心素养.
选做题:
5.观察函数![]() 的图象,借助计算工具,你能进一步缩小函数零点所在的范围吗?能否估算出此函数零点的近似值?若可以,请说出你的研究方法,并写出分析过程.
的图象,借助计算工具,你能进一步缩小函数零点所在的范围吗?能否估算出此函数零点的近似值?若可以,请说出你的研究方法,并写出分析过程.
设计意图:通过信息技术绘制图象,在零点存在定理的运用基础上积累探索“二分法”活动经验,为学生提供独立思考机会,发展学生的创新思维.落实“四基”、发展“四能”.
(七)教学反思
本节课是在类比一次函数、二次函数、幂函数等图象与性质的实际应用的研究方法和一般路径,使学生体会一般观念下的数学学习,提升解决问题的本领;类比二次函数的零点的研究方法进行函数零点的概念的探究,学生很容易做到,但对零点存在定理的两个条件“在规定区间![]() 上连续”和“
上连续”和“![]() ”的理解有些困难,可以安排学生对教材第147页的“阅读与思考”进行学习,补充定理的证明思路,或者学生自主学习课外读物,在应用环节可以多举例子,利用计算机软件画出图象,结合图象的特征对函数的性质进行深入学习.
”的理解有些困难,可以安排学生对教材第147页的“阅读与思考”进行学习,补充定理的证明思路,或者学生自主学习课外读物,在应用环节可以多举例子,利用计算机软件画出图象,结合图象的特征对函数的性质进行深入学习.
【小单元教案】高中数学人教A版(2019)必修第一册--5.4.4 正切函数的性质与图象(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--5.4.4 正切函数的性质与图象(课时教学设计),共9页。
【小单元教案】高中数学人教A版(2019)必修第一册--4.4.3 不同函数增长的差异(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--4.4.3 不同函数增长的差异(课时教学设计),共7页。教案主要包含了目标检测设计等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.1 指数优质教案设计: 这是一份高中数学人教A版 (2019)必修 第一册4.1 指数优质教案设计,共4页。













