【小单元教案】高中数学人教A版(2019)必修第一册--5.1 任意角和弧度制（单元教学设计）

课题：5.1 任意角和弧度制单元教学设计

一、教学内容及其解析

（一）   内容

任意角和弧度制的概念、弧度与角度的互换.

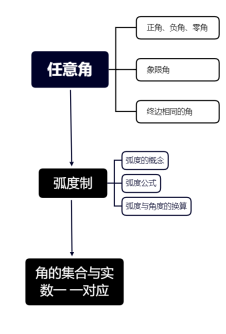本单元结构图如下:

(二) 内容解析

1.内容本质：本单元的内容本质是为后面学习任意角的三角函数做铺垫.因为是任意角，所以必须把初中阶段学的0°～360°扩展到任意角，教材是从实际生活现象入手说明推广到任意角的必要性以及角可以通过圆周运动的旋转来定义任意角，进而得到正角、负角、零角以及象限角和终边相同的角的概念. 由于函数自变量是在实数范围内，实数是十进制数，而角度制是60进制数，所以需要把角的大小用实数来表示.弧度制本质上就是用长度来刻画角度大小，教材通过类比其他物理量有不同的单位制表示，说明角度的大小也可以用不同的单位制表示，然后利用初中学过的弧长公式变形发现弧长与半径的比值只与角度有关，从而得到弧度制的概念以及与角度制的换算公式.

2.蕴含的思想方法：本单元的思想方法主要是数学抽象和函数的思想.从现实生活中抽象出任意角的概念，利用弧长与半径的比值与所对的圆心角的角度是一一对应的函数关系来定义弧度制.

3.知识的上下位关系：本单元是在建立在学生在初中阶段学过0°～360°和弧长公式的基础上，结合函数一一对应的思想得到任意角和弧度制的概念及换算，是为了学习任意角的三角函数做铺垫。

4.育人价值：通过对实际生活中的圆周运动和超过360°角的实例抽象出任意角的定义，发展学生的数学抽象素养；通过弧长公式的变形和函数一一对应观点得到弧度制的概念及换算公式，发展学生函数思想和数学运算素养.

5.教学重点： 任意角、弧度制的概念，弧度制与角度制的换算.

二、目标及其解析

（一）单元目标

1.了解任意角的定义，知道象限角和终边相同的角的概念及其表示;

2.了解弧度制的定义，能进行角度与弧度的互化;

3.体会引入弧度制的必要性.

（二）目标解析

达成上述目标的标志是: 

1.在具体的问题中能判断任意角所在的象限，并能够用集合语言描述某个终边相同的角;

2.会推导弧长公式，在具体的问题中，会进行角度与弧度的互化.

3.知道角度制单位与弧度制单位不同，了解在弧度制下，角的集合与实数集之间建立起一一对应的关系；能利用弧度制证明有关扇形的公式，体会弧度制带来的便利.

三、教学问题诊断分析

问题1 终边相同的角的表示

破解方法：对于初学的学生来说，终边相同的角的表示是很多同学难以理解的点，在教学中可以从具体实例入手，先写出一些具体的终边相同的角，然后归纳总结其一般共性，用字母代替数字，最终得到终边相同的角的集合表示.

问题2 对弧度制定义的理解

破解方法：由于学生都是用角度制来描述角的大小，所以现在提出一个新的单位制来描述角的大小，可能有些不适应，所以可让学生自己先推导初中阶段学过的弧长公式，在教师的引导下，作适当的变形，发现弧长与半径之比只有角度有关，从而暗示学生可以用弧长与半径之比来刻画角度大小，进而得到弧度制的概念. 单从定义上来看，很多学生对于1弧度的角的大小缺乏一个直观的认识，这时可以考虑借助网络画板作出一个动态图像，给学生直观地感受.

（动态图像地址： https://www.netpad.net.cn/resource_web/course/#/664393）

本单元教学难点：终边相同的角的表示及弧度制概念的理解.

四、教学支持条件分析

1. 初中阶段学生已经学习了0°～360°范围的角和用角度值刻画角的大小，所以从实际生活中和类比其单位制可以自然地引入任意角和弧度制的概念，教师在这个过程中主要就是提供素材和问题，让学生感受思考，自主学习，遇到关键问题时作适当引导。

2.硬件支持是导学案和信息技术作图软件，推荐使用网络画板展示任意角及任意弧度的角

五、课时分配设计

本单元共2课时，具体分配如下：

第1课时，任意角

第2课时，弧度制