- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2 三角函数的概念(单元教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2.1 三角函数的定义域和函数值的符号规律(第2课时)(课时教学设计) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2.2 同角三角函数的基本关系(第3课时)(课时教学设计1) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2.2 同角三角函数的基本关系(第3课时)(课时教学设计2) 教案 2 次下载
- 【小单元教案】高中数学人教A版(2019)必修第一册--5.2.2 同角三角函数的基本关系(第3课时)(课时教学设计3) 教案 2 次下载
高中数学人教A版 (2019)必修 第一册5.2 三角函数的概念获奖第1课时教学设计
展开(一)教学内容
(二)教学目标
通过数学抽象,能够将匀速圆周运动归结到单位圆上的点的运动规律的刻画,借助单位圆上点的坐标定义三角函数,进而建立三角函数的概念, 体会数形结合思想方法的作用,发展直观想象、数学抽象等核心素养.
(三)教学重点及难点
1.教学重点:任意角的三角函数概念.
2.教学难点:如何建立任意角的三角函数概念.
 (四)教学过程设计
(四)教学过程设计
![]() 引导语 :现实世界中存在着各种各样的“周而复始”的变化现象,圆周运动是这类现象的代表,如右图1所示,☉
引导语 :现实世界中存在着各种各样的“周而复始”的变化现象,圆周运动是这类现象的代表,如右图1所示,☉![]() 上的点
上的点![]() 以
以![]() 为起点做逆时针旋转,在弧度制下,我们已经将角的范围扩展到全体实数,能否建立一个函数模型,刻画点
为起点做逆时针旋转,在弧度制下,我们已经将角的范围扩展到全体实数,能否建立一个函数模型,刻画点![]() 的位置变化情况?
的位置变化情况?
师生活动:教师提出问题,学生独立思考后,在已有的研究函数的经验基础上能够给出研究路径:明确研究背景--对应关系的特点分析--下定义--性质.
追问:要解决这个问题,我们需要什么工具?
学生能够说出建立函数模型,需要利用直角坐标系,并先研究单位圆上点的运动,
如图,以单位圆的圆心![]() 为坐标原点,以射线
为坐标原点,以射线![]() 为
为![]() 轴的非负半轴,建立直角坐标系,点
轴的非负半轴,建立直角坐标系,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() . 把该问题抽象为一个质点
. 把该问题抽象为一个质点![]() 从点
从点![]()
![]() 开始在单位圆上的运动.
开始在单位圆上的运动.
问题1:当![]() 时,点P的坐标是什么?当
时,点P的坐标是什么?当![]() 或
或![]() 时,点P的坐标又是什么?它们是唯一确定的吗?
时,点P的坐标又是什么?它们是唯一确定的吗?
师生活动:教师提出问题后,学生进行讨论.利用勾股定理可以发现,当 =![]() 时,点
时,点![]() 的坐标是
的坐标是![]() ;当
;当![]() 或
或![]() 时,点
时,点![]() 的坐标分别是(0,1)和
的坐标分别是(0,1)和![]() .它们都是唯一确定的.
.它们都是唯一确定的.
设计意图:先研究特殊角下点![]() 坐标,再研究任意角下点
坐标,再研究任意角下点![]() 坐标.体现由特殊到一般的思想.
坐标.体现由特殊到一般的思想.
问题2:一般地,任意给定一个角![]() ,它的终边
,它的终边![]() 与单位圆交点
与单位圆交点![]() 的坐标能唯一确定吗?
的坐标能唯一确定吗?
 师生活动:教师提出问题后,学生进行讨论.因为单位圆的半径不变,点
师生活动:教师提出问题后,学生进行讨论.因为单位圆的半径不变,点![]() 的坐标只与角
的坐标只与角![]() 的大小有关,当角
的大小有关,当角![]() 确定时,点
确定时,点![]() 的坐标是
的坐标是![]() 也唯一确定.
也唯一确定.
追问1:用GGB动态展示角![]() 变化的过程,观察角
变化的过程,观察角![]() 的终边
的终边![]() 与单位圆的交点
与单位圆的交点![]() 的坐标,有什么发现?能运用函数的语言刻画这种对应关系吗?
的坐标,有什么发现?能运用函数的语言刻画这种对应关系吗?
师生活动:对任意一个实数![]() ,它的终边
,它的终边![]() 与单位圆的交点
与单位圆的交点![]() 的横、纵坐标
的横、纵坐标![]() 都是唯一确定的,有如下对应关系:
都是唯一确定的,有如下对应关系:
![]() 任意角
任意角![]() (弧度)→ 唯一实数
(弧度)→ 唯一实数![]() ;
;
![]() 任意角
任意角![]() (弧度)→ 唯一实数
(弧度)→ 唯一实数![]() .
.
一般地,任意给定一个角![]() ,它的终边
,它的终边![]() 与单位圆交点
与单位圆交点![]() 的坐标,无论是横坐标
的坐标,无论是横坐标![]() ,还是纵坐标
,还是纵坐标![]() ,都是唯一确定的.所以,点
,都是唯一确定的.所以,点![]() 的横坐标
的横坐标![]() 、纵坐标
、纵坐标![]() 都是角
都是角![]() 的函数.
的函数.
设计意图:以函数的对应关系为指向,从特殊到一般,使学生确认相应的对应关系满足函数的定义,角的终边与单位圆的交点的横、纵坐标都是圆心角![]() (弧度)的函数,为引出三角函数的定义做好铺垫.
(弧度)的函数,为引出三角函数的定义做好铺垫.
问题3:通过阅读教科书第177-178页,你能给出三角函数的定义吗?
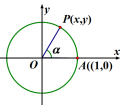 师生活动:教师给出图示,学生结合图中信息给出三个定义,设
师生活动:教师给出图示,学生结合图中信息给出三个定义,设![]() 是一个任意角
是一个任意角![]() ,它的终边
,它的终边![]() 与单位圆相交于点
与单位圆相交于点![]() ,那么把点
,那么把点![]() 的纵坐标
的纵坐标![]() 叫做
叫做![]() 的正弦函数,记做
的正弦函数,记做![]() ,即
,即![]() ;
;
把点![]() 的横坐标
的横坐标![]() 叫做
叫做![]() 的余弦函数,记做
的余弦函数,记做![]() ,即
,即![]() ;
;
把点![]() 的纵坐标与横坐标的比值
的纵坐标与横坐标的比值![]() 叫做
叫做![]() 的正切函数,记做
的正切函数,记做![]() ,即
,即![]() .
.
可以看出,当 =![]() (
(![]() )时,
)时,![]() 的终边在
的终边在 ![]() 轴上,这时点
轴上,这时点![]() 的横坐标 x 等于0,所以
的横坐标 x 等于0,所以![]() =
= ![]() 无意义.除此之外,对于确定的角
无意义.除此之外,对于确定的角![]() ,
,![]() 的值也是唯一确定的.所以,
的值也是唯一确定的.所以,![]() =
= ![]() (x≠0)也是以角为自变量,以单位圆上点的纵坐标与横坐标的比值为函数值的函数,称为正切函数.
(x≠0)也是以角为自变量,以单位圆上点的纵坐标与横坐标的比值为函数值的函数,称为正切函数.
追问1:符号![]() ,
,![]() 和
和![]() 分别表示什么?在之前有过类似的引入特定符号表示一种量的经历吗?
分别表示什么?在之前有过类似的引入特定符号表示一种量的经历吗?
学生独立思考,能回忆并类比已有知识,(引入符号![]() )理解三角函数符号的意义.
)理解三角函数符号的意义.
追问2:任意角三角函数的定义域分别是什么呢?
学生进行讨论.正弦函数和余弦函数的定义域都是实数集,即![]() ,对于正切函数而言,要求点
,对于正切函数而言,要求点![]() 的横坐标
的横坐标![]() ,即角
,即角![]() 的终边
的终边![]() 不能位于
不能位于![]() 轴上,那么正切函数的定义域为
轴上,那么正切函数的定义域为![]() .
.
设计意图:在问题的引导下,通过阅读教科书使学生对三角函数定义有更深刻的理解.
问题4: 任意角三角函数的定义是否符合高中函数的定义呢?
师生活动:教师提出问题后,学生进行讨论.正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或者坐标的比值为函数值的函数.由于角的集合与实数集之间可以建立一一对应关系, 所以三角函数可以看成是自变量为实数的函数.
按照函数的定义与常用的符号,我们通常将它们记为
正弦函数 y = sinx,x∈R;
余弦函数 y = cosx,x∈R;
正切函数 y = tanx,x≠![]() (
(![]() )
)
将正弦函数、余弦函数和正切函数统称为三角函数.
追问1:这个定义相对于锐角三角函数的定义有什么不同呢?
师生活动:任意角的三角函数是通过角与单位圆交点的坐标定义的,锐角三角函数是通过直角三角形边长的比值定义的,在单位圆中直角三角形斜边为1,所以锐角三角函数也可用角的终边与单位圆交点的坐标定义,此时终边上的点都在第一象限,因此锐角三角函数值都是正数,而任意角的三角函数值可以是负数.
 设计意图:引导学生将任意角三角函数纳入到函数中,丰富学生对三角函数的认知,另外,注意任意角为轴线角的特殊情况,让学生更全面地认识任意角的三角函数,体现数学的严谨性.
设计意图:引导学生将任意角三角函数纳入到函数中,丰富学生对三角函数的认知,另外,注意任意角为轴线角的特殊情况,让学生更全面地认识任意角的三角函数,体现数学的严谨性.
问题5:求![]() 的正弦、余弦和正切值.
的正弦、余弦和正切值.
师生活动:先由学生说思路,再引导从学生回归三角函数定义总结求三角函数值的基本步骤,完成解答.
所以![]()
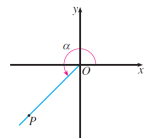 设计意图:通过概念的简单应用,明确用定义求三角函数值的基本步骤,进一步理解定义的内涵.
设计意图:通过概念的简单应用,明确用定义求三角函数值的基本步骤,进一步理解定义的内涵.
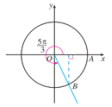
问题6:如图,设![]() 是一个任意角,它的终边上任意一点
是一个任意角,它的终边上任意一点![]() (不与原点
(不与原点![]() 重合)的坐标为
重合)的坐标为![]() ,点
,点![]() 与原点的距离为
与原点的距离为![]() .
.
求证:![]() ,
,![]() ,
,![]()
师生活动:给出问题后,教师可以引导学生分析以下问题,再让学生给出证明思路.
①你能根据三角函数的定义作图表示![]() 和
和![]() 吗?
吗?
②在你所作的图形中,![]() ,
,![]() ,
,![]() 表示什么?你能找到它们与任意角
表示什么?你能找到它们与任意角![]() 的三角函数的关系吗?
的三角函数的关系吗?
解:设角![]() 的终边与单位圆交于点
的终边与单位圆交于点![]()
![]() ,分别过点
,分别过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足分别为
,垂足分别为![]() ,
,
 则
则![]() ,
,![]()
![]()
![]()
![]() .
.![]()
所以得到![]() , 即
, 即![]() .
.
因为![]() 与
与![]() 同号,所以
同号,所以![]() ,即
,即![]() .
.
同理可证:![]() ,
,![]() .
.
设计意图:通过问题引导,使学生找到![]() 、
、![]() ,并利用它们的相似关系,根据三角函数的定义得到证明.
,并利用它们的相似关系,根据三角函数的定义得到证明.
(五)课堂小结
问题7:你怎样建立三角函数的概念?如何理解三角函数符号的意义?经历三角函数概念的学习过程你体会到了哪些数学思想?
师生活动:学生回答,若不完整,再请其他的同学进行补充.
设计意图:回顾本节课所学内容和学习过程,感悟本节课涉及的数学思想方法,交流分享关于本节课的收获.
(六)目标检测设计
1.求π的正弦、余弦和正切值.
[解析] 在直角坐标系中作∠AOB=π,如图.
∠AOB的终边OB与单位圆的交点B. 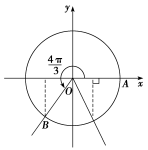
坐标为,
∴sinπ=-,cosπ=-,tanπ=.
2.若角![]() 的终边经过点P(5,-12),则sin
的终边经过点P(5,-12),则sin![]() =________,cos
=________,cos![]() =________,tan
=________,tan![]() =________.
=________.
解析:∵x=5,y=-12,∴r==13,
则sin![]() ==-,cos
==-,cos![]() ==,tan
==,tan![]() ==-.
==-.
设计意图:通过课堂达标练习,让学生及时巩固所学,让学生理解任意角的三角函数定义,培养数学抽象的核心素养.
【小单元教案】高中数学人教A版(2019)必修第一册--5.6.1 函数y=Asin(wx b)的图象(第1课时)(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--5.6.1 函数y=Asin(wx b)的图象(第1课时)(课时教学设计),共3页。
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式一等奖第1课时教学设计: 这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式一等奖第1课时教学设计,共4页。
【小单元教案】高中数学人教A版(2019)必修第一册--5.2.1 三角函数的定义域和函数值的符号规律(第2课时)(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)必修第一册--5.2.1 三角函数的定义域和函数值的符号规律(第2课时)(课时教学设计),共4页。