【小单元教案】高中数学人教A版(2019)必修第一册--5.2.2 同角三角函数的基本关系（第3课时）（课时教学设计3）

课题：5.2.2 同角三角函数的基本关系教学设计（第3课时）

（一）教学内容   

《普通高中数学必修第一册》人教A版（2019）第五章《三角函数》的第二节《三角函数的概念》

(二）教学目标

1.能根据三角函数的定义推导同角三角函数的基本关系式，培养数学抽象的核心素养 

2.掌握同角三角函数的基本关系式，并能根据一个角的三角函数值，求其它三角函数值，提升数学运算的核心素养；

3.会利用同角三角函数的基本关系式进行化简、求值与恒等式证明，提升数学运算的核心素养。（三）教学重点及难点

重点：理解并掌握同角三角函数基本关系式的推导及应用；

难点：会利用同角三角函数的基本关系式进行化简、求值与恒等式证明．

（四）教学过程设计（主体内容）

用问题分解教学目标

1.课题导入

1. 创设情境，生成问题

气象学家洛伦兹1963年提出一种观点：南美洲亚马逊河流域热带雨林中的一只蝴蝶，偶尔扇动几下翅膀，可能在两周后引起美国德克萨斯的一场龙卷风.这就是理论界闻名的“蝴蝶效应”，此效应本意是说事物初始条件的微弱变化可能会引起结果的巨大变化.蝴蝶扇翅膀成为龙卷风的导火索.从中我们还可以看出，南美洲亚马逊河流域热带雨林中的一只蝴蝶与北美德克萨斯的龙卷风看来是毫不相干的两种事物，却会有这样的联系，这也正验证了哲学理论中事物是普遍联系的观点.

想一想：既然感觉毫不相干的事物之间都是相互联系的，那么“同一个角”的三角函数之间有没有关系呢？

提示：有.

2.探究教学

设角α的终边与单位圆交于点P(x,y),根据三角函数的定义知y=sin α,x=cos α,   =tan α.

【探究1】能否根据x,y的关系得到sin α,cos α,tan α的关系?

【提示】sin2α＋cos2α＝1,＝tan_α.

【探究2】公式sin2α＋cos2α＝1与＝tan_α对任意角都成立吗?

【提示】sin2α＋cos2α＝1对任意角α均成立,当α≠kπ+   ,k∈Z时,＝tan_α    成立.

【设计意图】通过复习三角函数的定义，用联系的观点引入本节新课，建立知识间的联系，提高学生概括推理的能力。

（二）同角三角函数的基本关系

同角三角函数的基本关系

(1)平方关系：sin2α＋cos2α＝1；

(2)商数关系：＝tan_α(α≠＋kπ，k∈Z)．

(3)文字叙述：同一个角α的正弦、余弦的平方和等于1，商等于角α的正切．

【思考】“同角”一词的含义是什么？

【提示】　一是“角相同”，如sin2α＋cos2β＝1就不一定成立．二是对任意一个角(在使得函数有意义的前提下)，关系式都成立，即与角的表达式形式无关，如sin215°＋cos215°＝1，sin2＋cos2＝1等．

【做一做1】已知α是第四象限角，cos α＝，则sin α＝       .

【答案】　－

【做一做2】sin2＋cos2＝      .

【答案】 1

【做一做3】已知3sin α＋cos α＝0，则tan α＝       .

【答案】－

拓展：基本关系式的变形公式

sin2α＋cos2α＝1⇒

tan α＝⇒

【设计意图】通过探究让学生理解探究三角函数的基本关系，提高学生分析问题的能力。

（三）典型例题

1.已知一个三角函数值求另两个三角函数值

例1.已知cos α＝－，角 α在第二象限，求sin α，tan α的值．

【解析】α是第二象限角时，sin α>0，tan α<0，

∴sin α＝＝ ＝，

tan α＝＝＝－.

【变式探究1】将本例条件“角 α在第二象限”去掉，求sin α，tan α的值．

[解析]　∵cos α＝－<0，∴α是第二或第三象限角．

当α是第二象限角时，sin α>0，tan α<0，∴sin α＝＝ ＝，

tan α＝＝＝－.

当α是第三象限角时，sin α<0，tan α>0，∴sin α＝－＝ －＝－，

tan α＝＝.

【变式探究2】已知tan α＝－2，求sin α，cos α的值．

[解析]　法一：∵tan α＝－2<0，

∴α为第二或第四象限角，且sin α＝－2 cos α，①

又sin2α＋cos2α＝1，②

由①②消去sin α，得(－2cos α)2＋cos2α＝1，即cos2α＝；

当α为第二象限角时，cos α＝－，代入①得sin α＝；

当α为第四象限角时，cos α＝，代入①得sin α＝－.

法二：∵tan α＝－2<0，∴α为第二或第四象限角．由tan α＝，

两边分别平方，得tan2α＝，又sin2α＋cos2α＝1，

∴tan2α＋1＝＋1＝＝，

即cos2α＝.

当α为第二象限角时，cos α<0，

∴cos α＝－ ＝－ ＝－，

∴sin α＝tan α·cos α＝(－2)×＝.

当α为第四象限角时，cos α>0，

∴cos α＝ ＝ ＝，

∴sin α＝tan α·cos α＝(－2)×＝－.

【类题通法】由某角的一个三角函数值求它的其余各三角函数值的依据及种类

(1)依据：cos α＝±或sin α＝±，要根据角α所在的象限，一般是先选用平方关系,再用商数关系，恰当选定根号前面的正负号，而在使用tan α＝时，不存在符号的选取问题．

(2)分类：

①如果已知三角函数的值，且角的象限已被指定时，则只有一组解；

②如果已知三角函数的值，但没有指定角在哪个象限，那么由已知三角函数值确定角可能在的象限，然后再求解，这种情况一般有两组解；

【巩固练习1】已知sin φ＝－，且|φ|＜，则tan φ＝(　　)

A．－　　　　　　　　 B．

C．－   D．

解析：选C　∵sin φ＝－，

∴cos2φ＝1－sin2φ＝1－2＝，

又|φ|＜，即－＜φ＜，

∴cos φ＝，从而tan φ＝＝＝－.

2.齐次式求值

例2. 已知tan α＝3，求：①；

②sin2α－3sin αcos α＋1.

[解析]　①原式＝＝＝1.

②原式＝＋1＝＋1

＝＋1＝0＋1＝1.

【类题通法】关于sin α,cos α的齐次式的求值方法

(1)关于sin α,cos α的齐次式,可以通过分子、分母同除以cos α或cos2α转化为关于tan α的式子后再求值.

(2)假如代数式中不含分母,可以视分母为1,灵活地进行“1”的代换,由1=sin2α+cos2α代换后,再同除以cos2α,构造出关于tan α的代数式.

【巩固练习2】已知＝－5，那么tan α的值为(　　)

A．－2  B．2

C.  D．－

解析：由＝－5，分子分母同除以cos α得：＝－5，解得tan α＝－.

答案：D

3.关于与的关系

例3.已知sin θ＋cos θ＝，且0＜θ＜π，求sin θ－cos θ.

[解析]　∵sin θ＋cos θ＝，

∴(sin θ＋cos θ)2＝，

解得sin θcos θ＝－.

∴(sin θ－cos θ)2＝1－2sin θcos θ＝.

∵0＜θ＜π，且sin θcos θ＜0，

∴sin θ＞0，cos θ＜0，

∴sin θ－cos θ＞0，

∴sin θ－cos θ＝.

【类题通法】(1)sin θ＋cos θ，sin θcos θ，sin θ－cos θ三个式子中，已知其中一个，可以求其他两个，即“知一求二”．

(2)求sin θ＋cos θ或sin θ－cos θ的值，开方时要注意判断它们的符号．

（3）sin θ±cos θ与sin θcos θ相互转化方法：(sin θ±cos θ)2＝1±2sin θcos θ.

【巩固练习3】若sin θ－cos θ＝，则tan θ＋＝        .

解析　由已知得(sin θ－cos θ)2＝2，

∴sin θcos θ＝－.

∴tan θ＋＝＋＝＝－2.

答案　－2

4.三角函数式的化简

例4.化简下列各式．

(1) tan α，其中α是第二象限角；

(2)

[解析]　(1)因为α是第二象限角，所以sin α>0，cos α<0.

故tan α＝tan α＝tan α

＝·＝·＝－1.

(2)原式＝

＝

＝

＝＝1.

【类题通法】1．三角函数式化简的本质及关注点

(1)本质：三角函数式化简的本质是一种不指定答案的恒等变换，体现了由繁到简的最基本的数学解题原则．

(2)关注点：不仅要熟悉和灵活运用同角三角函数的基本关系式，还要熟悉并灵活应用这些公式的等价变形，如sin2α＝1－cos2α，cos2α＝1－sin2α，1＝sin2α＋cos2α，sin α＝tan α·cos α，cos α＝.

2．对三角函数式化简的原则

(1)使三角函数式的次数尽量低．

(2)使式中的项数尽量少．

(3)使三角函数的种类尽量少．

(4)使式中的分母尽量不含有三角函数．

(5)使式中尽量不含有根号和绝对值符号．

(6)能求值的要求出具体的值，否则就用三角函数式来表示．

【巩固练习4】化简－得(　　)

A．－  B.  C．－  D.

解析　－＝＝＝－.

答案　A

5.三角函数式的证明

例5.求证：2(1－sin α)(1＋cos α)＝(1－sin α＋cos α)2.

[证明]　左边＝2(1－sin α＋cos α－sin αcos α)

＝1＋(sin2α＋cos2α)－2sin α＋2cos α－2sin αcos α

＝(1－2sin α＋sin2α)＋2cos α(1－sin α)＋cos2α

＝(1－sin α)2＋2cos α(1－sin α)＋cos2α

＝(1－sin α＋cos α)2＝右边．

∴原式成立．

【类题通法】证明三角恒等式的常用方法

证明恒等式的过程就是分析、转化、消去等式两边差异来促成统一的过程，证明时常用的方法有：

(1)从一边开始，证明它等于另一边，遵循由繁到简的原则．

(2)证明左右两边等于同一个式子．

(3)证明左边减去右边等于零或左、右两边之比等于1.

(4)证明与原式等价的另一个式子成立，从而推出原式成立．

【巩固练习5】求证：sin4α－cos4α＝2sin2α－1.

证明：左边＝(sin2α＋cos2α)(sin2α－cos2α)＝sin2α－cos2α＝sin2α－(1－sin2α)＝2sin2α－1＝右边．

所以等式成立．

3.课堂小结：

 1.知识总结：

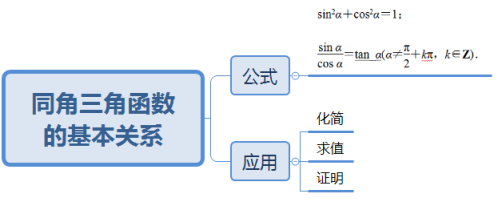
2.学生反思：

（1）通过这节课，你学到了什么知识？

（2）在解决问题时，用到了哪些数学思想？

【设计意图】

通过总结，让学生进一步巩固本节所学内容，提高概括能力,提高学生的数学运算能力和逻辑推理能力。

(五）目标检测设计

1.课堂检测

1．化简 的结果是(　　)

A．cos 　 B．－sin 　　

C．sin 　　 D．－cos

2．化简sin2α＋cos4α＋sin2αcos2α的结果是(　　)

A.  B.  C．1  D.

3．若α是三角形的内角，且sin α＋cos α＝，则此三角形是(　　)

A．钝角三角形   B．锐角三角形

C．直角三角形   D．等边三角形

4.化简(1＋tan2 α)·cos2 α＝________.

答案：1.C  2.C   3.A  4.1

【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。

2.课后作业

完成教材：第184页  练习     第1，2，3,4,5题

         第185页  习题5.2     第6,11,12,13,14,15,16题

（六）教学反思