【小单元教案】高中数学人教A版(2019)选修第一册--2.5.3 圆与圆的位置关系（课时教学设计）

第3课时 圆与圆的位置关系

（一）教学内容

圆与圆的位置关系

（二）教学目标

1.结合具体实例，并类比直线与圆的位置关系的研究思路和方法，能用坐标法法和几何法研究圆与圆的位置关系，发展学生类比能力.

2.通过对具体实例的分析研究，能体会坐标法在研究平面几何问题（如轨迹问题）的优越性，发展学生数形结合和数学建模的核心素养.

（三）教学重点

圆与圆的位置关系及判定方法

（四）教学难点

综合应用圆与圆的位置关系解决问题

（五）教学过程

   问题1 日食是一种天文现象，在民间称此现象为天狗食日。日食分为日偏食、日全食、日环食、全环食。我们将月亮与太阳抽象为圆，观察到的这些圆在变化的过程中位置关系是怎样的?

师生活动：学生回顾已学，得到两圆位置关系，相离，外切，相交，内切，内含.

设计意图：通过具体的情景，帮助学生回顾初中几何中已学的圆与圆的位置关系.  

问题2 类比运用直线和圆的方程，研究直线与圆的位置关系的方法，如何利用圆的方程，判断它们之间的位置关系？

师生活动：

（1）学生回顾初中所学圆与圆的位置关系的判定方法，类比直线与圆的位置关系的判定方法，自主归纳圆与圆的位置关系的判定方法.

（2）教师巡视全班并展示部分学生的做法：

1.几何法:

圆O1:(x-x1)2+(y-y1)2=(r1>0),圆O2:(x-x2)2+(y-y2)2=(r2>0),两圆的圆心距d=|O1O2|=,则有

2.代数法:圆O1:x2+y2+D1x+E1y+F1=0(-4F1>0),圆O2:x2+y2+D2x+E2y+F2=0(-4F2>0),两圆的方程联立得方程组,则有

设计意图：类比直线与圆的位置关系的研究圆与圆的位置关系.

问题3 已知圆，圆，判断圆与圆的位置关系.

　　师生活动：

　　学生独立解答，教师巡视全班，展示坐标法和几何法两种不同解法，并请学生对解答过程进行分析与解读.

追问 在坐标法中联立两圆方程后得到说明了什么？能据此判定两圆位置关系吗？呢？

设计意图：通过典例解析，帮助学生进一步熟悉两种基本方法，判断圆与圆的位置关系。同时在解答中引导学生由形助数，由数研形，发展学生数形结合能力及数学运算素养.

问题4 已知圆O的直径，动点M与点A的距离是它与点B的距离的倍.试探究点M的轨迹，并判断该轨迹与圆O的位置关系.

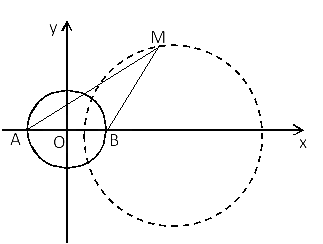
师生活动： 给出题目后，教师可以通过以下问题引导学生思考：

（1）如何建立平面直角坐标系？有哪些几何对象需要用坐标表示？

（2）问题中的几何对象之间有哪些关系，如何用坐标进行表示？

（3）说说你对动点M的轨迹及轨迹方程的理解？

让学生在独立思考的基础上解决问题，受圆的标准方程的建立的启发，考虑到对称性和让更多的几何对象落在坐标轴上，以线段AB的重点O为原点，AB所在直线为轴，线段AB中垂线为轴，建立坐标系，再将用两点间的距离公式表示列出方程，再对方程进行整理，化简，得到M点的轨迹方程，再对方程进行研究，发现它竟然表示的是圆，也就是说M点的轨迹是个圆！这是在没有得到M点方程的时候，很难想象的到的结果，这也正是坐标法的作用和价值.然后教师再用GGB生成M点的轨迹.

设计意图：本例是以数研形的典范，也是对坐标法解决平面几何问题的“三步曲”的再应用，通过建立动点的轨迹方程，判断动点轨迹，充分展现了坐标法的魅力；同时使用数学软件GGB，使学生清楚看到动点轨迹的形成过程，检验了方程。

追问：如果把本例中的“倍”改为“k倍”，你能分析解决这个问题吗？

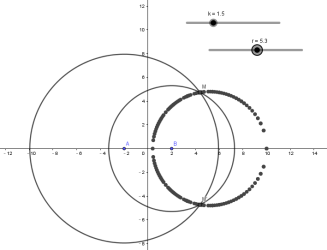
师生活动：教师先使用GGB中，作出探究M点轨迹的做法：作点A（-2,0），B（2,0），设置参数k,r,其中k控制MA与MB的长度之比，r控制圆B的半径；以B为圆心，r为半径作圆B，以A为圆心，k*r 为半径作圆A，圆A与圆B相较于M,改变r的值，就可以得到点M的轨迹。当改变k值后让学生观察动点M的轨迹是一个圆或是一条直线，当轨迹是圆的时候该圆的圆心和半径随着k值的改变而改变.

设计意图：本例中M的轨迹是一个圆，该圆被称为阿波罗尼圆.教学是根据学生的实际情况安排本环节.　

　 （六）目标检测设计

　　1.课堂练习

　   （1）已知圆C1:x2+y2+6x-4=0和圆C2:x2+y2+6y-28=0.

①求两圆公共弦所在直线的方程及弦长;

②求经过两圆交点且圆心在直线x-y-4=0上的圆的方程.

（2）已知两圆x2＋y2－2x－6y－1＝0，x2＋y2－10x－12y＋m＝0.

①m取何值时两圆外切？②m取何值时两圆内切？

③当m＝45时，求两圆的公共弦所在直线的方程和公共弦的长．

解析：因为两圆的标准方程分别为(x－1)2＋(y－3)2＝11，(x－5)2＋(y－6)2＝61－m，

所以两圆的圆心分别为(1,3)，(5,6)，半径分别为，，

①当两圆外切时，由＝＋，得m＝25＋10.

②当两圆内切时，因为定圆半径小于两圆圆心之间的距离5，所以－＝5，解得m＝25－10.③由(x2＋y2－2x－6y－1)－(x2＋y2－10x－12y＋45)＝0，得两圆的公共弦所在直线的方程为4x＋3y－23＝0.故两圆的公共弦的长为2 .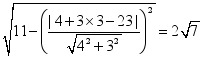

设计意图：通过圆与圆位置关系的综合问题，提升学生数学建模，数形结合，及方程思想，发展学生逻辑推理，直观想象、数学抽象和数学运算的核心素养。

2. 课后作业

教科书习题2.5第7，8，10题.

设计意图：巩固所学.