人教A版 (2019)选择性必修 第一册3.1 椭圆优秀教学设计及反思

3.1.3椭圆的简单几何性质 第1课时教学设计     

（一）教学内容   

利用椭圆的方程研究椭圆的简单几何性质

(二）教学目标

1.通过对椭圆图像的观察，能发现椭圆的简单几何性质，发展学生的直观想象素养。

2.经历椭圆简单几何性质的代数推导过程，获得利用代数方法证明几何性质的技能，发展学生的逻辑推理与数学运算素养。

3.在观察、发现、猜想、证明过程中，了解一般的数学发现及证明规律，体会严谨的数形结合思想。

（三）教学重点及难点

  重点：椭圆的简单几何性质

难点：通过椭圆的方程研究几何性质；理解椭圆的离心率。

（四）教学过程设计（主体内容）

1、创设情境，发现问题

问题1：我们是怎样研究圆的？

生：圆的方程和几何性质。

追问：我们学习了椭圆的哪些知识，接下来要研究什么？

生：学习了椭圆的定义和标准方程，接下来要研究椭圆的几何性质。

追问：研究椭圆的哪些性质呢？

生1:形状、大小、对称性、特殊点。

追问：如何研究呢？

生2：图像，应该还与方程有关。

教师：没错，就是要用图形和代数两个方面去研究椭圆的性质。数学家华罗庚说过“数少形时少直观，形缺数时难入微”，我们今天借助上节课学习的椭圆的标准方程研究椭圆的几何性质。

设计意图：创建数学情境，引导学生通过圆的方程和性质类比发现问题——椭圆有怎样的简答几何性质，明确研究的基本思想和方法，先形后数，体会数形结合的思想。

2、数学探究，解决问题

教师：为了研究方便，以椭圆为例。

探究1：范围

问题2：圆的方程确定时，横纵坐标有范围。那么椭圆有范围吗？如何寻找范围呢？

学生活动：独立思考后讨论探究。

生1：椭圆的范围就是利用椭圆的方程确定椭圆上点的横、纵坐标的取值范围。我采用有界性的方法：

，则；同理，。

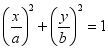生2：因为，联系到，，利用三角函数的有界性，可求得范围。

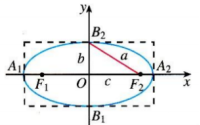
教师：通过以上的分析，大家知道椭圆位于直线与直线所围成的举行区域。与课本的图形也相符。

设计意图：学生类比圆，明确研究椭圆的范围实质上是研究坐标范围，明确研究的途径是先观察，在用方程证明，经历形到数的探究过程，体会利用方程研究几何性质的便利性和严谨性。

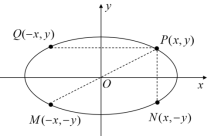探究2：对称性

问题3：对于椭圆，已知点在椭圆上，你能说出椭圆上还有哪些点吗？

生3：、、。

追问：一个点的坐标是无法求解椭圆的方程的，你是如何计算的呢？

生3：改变数的正负，对平方运算没有影响。

追问：这些点有什么关系

生4：关于坐标轴或者原点对称。

追问:由点的任意性，能够说明椭圆关于坐标轴或者原点对称吗？如何证明？

生5：从代数的角度说明，

把换成方程不变，说明椭圆关于对称；把换成方程不变，说明椭圆关于对称；

把换成，换成方程不变，说明椭圆关于对称；

教师：没错，可以从代数角度进行说明。将椭圆的对称中心叫做椭圆的中心。

设计意图：学生容易由形归纳出椭圆的对称性。但是用代数法证明较难想到。由特殊到一般，引导学生研究椭圆的对称性，追问引导，促使学生明确对称性的实质和如何利用椭圆方程判断椭圆的对称性，发展学生的逻辑推理素养。

探究3：顶点

问题4：我们可以利用直线与直线来确定椭圆的位置。能否利用特殊的点来确定椭圆的位置吗？如果可以的话，你认为那些点比较特殊？如何得到他们的坐标？

生6：横纵坐标取最值时的点比较特殊。所以可以取、、、

教师：我们将椭圆和坐标轴的四个交点称为椭圆的顶点，将线段,分别叫做椭圆的长轴和短轴，长轴长，短轴长，和分别叫做椭圆的长半轴长和短半轴长。

学生活动：

在同一个坐标系下利用描点法做出下列椭圆的草图：

（1）；（2）

设计意图：

探究性质的过程即为特殊化的过程，教师问题引导，学生经历特殊化的过程，再通过学生动手操作，利用几何性质作出椭圆的草图，进一步体会数形结合思想，发展学生数学抽象素养。给出的两个椭圆“圆扁”程度不同，为下面引入椭圆的离心率埋下伏笔。

探究4：离心率

  问题5：所有的圆都是相似的，椭圆也是的吗？刚才画的两个椭圆有“圆”、有“扁”。从椭圆方程的角度看，如何刻画椭圆“扁”的程度呢？

生7：我认为可以用的大小衡量椭圆的“圆扁”程度。

生8：我认为可以用的大小衡量椭圆的“圆扁”程度。

教师geogebra软件演示两者变化时椭圆的变化情况。

追问：刚才画的两个椭圆及演示已经可以推测当一定时，越大时，椭圆越“圆”；越小时，椭圆越“扁”。有没有同学能够能够给一个一般的说明。

生7：从方程的角度看，更直观一些，因为椭圆在长为，宽为的矩形中，矩形越扁，椭圆越“扁”，矩形越接近于正方形，椭圆越“圆”。 恰好为矩形一条对角线的斜率，矩形的形状可以由它来刻画。

追问：对于应该如何解释？

生9：因为，所以。当越大时，越小，此时椭圆越“圆”; 当越小时，越大，此时椭圆越“扁”。

教师：原来两者都可以刻画椭圆的“圆扁”程度，基于最原始的定义和后续的学习，我们把叫做椭圆的离心率，可以描述椭圆的扁平程度。离心率的变化范围是什么？是怎样影响椭圆形状？

学生10：，当越接近时，越大，椭圆越“扁”； 当与相差较大时，越小，椭圆越“圆”；

设计意图：

椭圆的形状可以利用椭圆方程的参数确定，geogebra软件直观展示，通过问题引导学生思考、辨析，经历观察、猜想、验证的思维过程，培养学生严谨的数学思维习惯，发展学生逻辑推理素养。

3、数学应用，内化迁移

例1： 求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标.

解：椭圆的标准方程为，所以

所以椭圆的长轴长为，短轴长为，离心率，，

两个焦点为，四个顶点坐标为，

例2：已知平面直角坐标系中有一条曲线的方程为，关于曲线的对称性，下列说法正确的是（     ）

A、关于轴对称             B、关于轴对称

C、关于原点对称             D、不具有对称性

设计意图：促进学生掌握椭圆的几何性质和判断曲线对称性的基本方法，提高学生分析问题、解决问题的能力。

4、回顾反思，提炼升华

问题6：(1)椭圆的简单几何性质有哪些？

(2)我们如何研究椭圆的几何性质

设计意图：及时梳理、提炼与升华所学知识.

（五）作业分层，因材施教

（1）写出椭圆的简单几何性质

（2）完成课本练习1、2、3、4、5                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                      

（六）教学反思