【同步练习】高中数学人教A版(2019)必修第二册--10.1.2事件的关系和运算 课时作业（含解析）

10．1.1　有限样本空间与随机事件10．1.2　事件的关系和运算

必备知识基础练　

1．下列事件属于随机事件的是(　　)

A．函数y＝logx在定义域内为增函数

B．马龙和王楚钦打乒乓球，王楚钦胜利

C．998名学生中至少有3名学生的生日相同

D．在标准大气压下，河流在20 ℃时结冰

2．抛掷两枚骰子各一次，记第一枚骰子掷出的点数与第二枚骰子掷出的点数之差为X，则“X≥5”对应的样本点是(　　)

A．(6，2)    B．(5，1)

C．(1，6)    D．(6，1)

3．下列事件中，不可能事件是(　　)

A．三角形内角和为180°

B．三角形中大边对大角，小边对小角

C．锐角三角形中两个内角和等于90°

D．三角形中任意两边之和大于第三边

4．下列事件是必然事件的是(　　)

A．从分别标有数字1，2，3，4，5的5张标签中任取一张，得到标有数字4的标签

B．函数y＝logax(a>0且a≠1)为增函数

C.平行于同一条直线的两条直线平行

D．随机选取一个实数x，得2x<0

5．抛掷一枚骰子，“向上的点数是1或2”为事件A，“向上的点数是2或3”为事件B，则(　　)

A．A⊆B

B．A＝B

C．A＋B表示向上的点数是1或2或3

D．AB表示向上的点数是1或2或3

6．一个人连续射击目标2次，则下列选项中与“至少有一次击中”为对立事件的是(　　)

A．两次均击中    B．恰有一次击中

C．第一次击中    D．两次均未击中

7．抛掷一枚质地均匀的骰子两次，事件M＝{(2，6)，(3，5)，(4，4)，(5，3)，(6，2)}，则事件M的含义是________．

8．同时抛掷两枚质地均匀的硬币，记事件A＝{(正，反)}，写出事件A的一个互斥事件________．(用集合表示，写出一个即可)

关键能力综合练　

1．一个家庭有两个小孩，则样本空间为(　　)

A．{(男，女)，(男，男)，(女，女)}

B．{(男，女)，(女，男)}

C．{(男，男)，(男，女)，(女，男)，(女，女)}

D．{(男，男)，(女，女)}

2．命题“事件A与事件B对立”是命题“事件A与事件B互斥”的(　　)

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

3．一个射手进行射击，记事件A1＝“脱靶”，A2＝“中靶”，A3＝“中靶环数大于4”，则在上述事件中，互斥而不对立的事件是(　　)

A．A1与A2    B．A1与A3

C．A2与A3    D．以上都不对

4．对空中飞行的飞机连续射击两次，每次发射一枚炮弹，设A＝“两次都击中飞机”，B＝“两次都没击中飞机”，C＝“恰有一枚炮弹击中飞机”，D＝“至少有一枚炮弹击中飞机”，下列关系不正确的是(　　)

A．A⊆D

B．B∩D＝∅

C．A∪C＝D

D．A∪B＝B∪D

5．(多选)一个盒子中装有5支圆珠笔，其中3支一等品，2支二等品，大小质地完全相同，若从中随机取出3支，则与事件“取出1支一等品和2支二等品”互斥的事件有(　　)

A．取出的3支笔中，至少2支一等品

B．取出的3支笔中，至多1支二等品

C．取出的3支笔中，既有一等品也有二等品

D．取出的3支笔中，没有二等品

6．(多选)不透明的口袋内装有红色、绿色和蓝色卡片各2张，一次任意取出2张卡片，则与事件“2张卡片都为红色”互斥而不对立的事件有(　　)

A．2张卡片不全为红色

B．2张卡片恰有一张红色

C．2张卡片至少有一张红色

D．2张卡片都为绿色

7．从长度为2，4，5，7，9的五条线段中任取三条(抽取不分先后)，设事件A＝“取出的三条线段能构成一个三角形”，则事件A包含的样本点个数为________个．

8．在10件产品中有8件一级品，2件二级品，从中任取3件，若记“3件都是一级品”为事件A，则A的对立事件是________________．

9．用红、黄、蓝三种不同的颜色给大小相同的三个圆随机涂色，每个圆只涂一种颜色．设事件A＝“三个圆的颜色全不相同”，事件B＝“三个圆的颜色不全相同”，事件C＝“其中两个圆的颜色相同”，事件D＝“三个圆的颜色全相同”．

(1)写出试验的样本空间；

(2)用集合的形式表示事件A，B，C，D；

(3)事件B与事件C有什么关系？事件A和B的交事件与事件D有什么关系？并说明理由．

10.某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，判断下列每对事件是不是互斥事件，如果是，再判别它们是不是对立事件．

(1)恰有1名男生与恰有2名男生；

(2)至少有1名男生与全是男生；

(3)至少有1名男生与全是女生；

(4)至少有1名男生与至少有1名女生．

核心素养升级练　

1．从装有两个红球和两个白球的口袋内任取两个球，那么互斥而不对立的事件是(　　)

A．至少有一个白球与都是红球

B．恰好有一个白球与都是红球

C．至少有一个白球与都是白球

D．至少有一个白球与至少一个红球

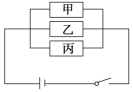
2．如图所示，事件A＝“甲元件正常”，B＝“乙元件正常”，C＝“丙元件正常”．则A∪B∪C表示的含义为________，A∩B∩C表示的含义为________．

3．掷一个骰子，下列事件：A＝{出现奇数点}，B＝{出现偶数点}，C＝{出现点数小于3}，D＝{出现点数大于2}，E＝{出现点数是3的倍数}．求：

(1)A∩B, B∩C；

(2)A∪B，B∪C；

(3)记是事件H的对立事件，求，∩C，∪C，∪.

10．1.1　有限样本空间与随机事件

10．1.2　事件的关系和运算

必备知识基础练

1．答案：B

解析：函数y＝logx应为单调减函数，说法不正确，故A为不可能事件；

可能马龙胜利也可能王楚钦胜利，故B为随机事件；

998大于365的两倍，说法正确，故C为必然事件；

对于D，说法不正确，故为不可能事件．

故选B.

2．答案：D

解析：连续抛掷两枚骰子，第一枚骰子和第二枚骰子点数之差是{X|－5≤X≤5，X∈Z}，则“X≥5”对应的样本点是(6，1)，故选D.

3．答案：C

解析：由三角形性质可知A、B、D为必然事件；

由三角形内角和定理知两个内角和等于90°的三角形为锐角三角形是不可能的，所以C为不可能事件．

故选C.

4．答案：C

解析：A是随机事件，5张标签都可能被取到．

B是随机事件，当a>1时，函数y＝logax为增函数，当0<a<1时，函数y＝logax为减函数．

C是必然事件，实质是平行公理．

D为不可能事件，根据指数函数y＝2x的图象可得，对任意实数x，都有2x>0.

选故C.

5．答案：C

解析：由题意，可知A＝{1，2}，B＝{2，3}，

则A∩B＝{2}，A∪B＝{1，2，3}，

∴A∪B表示向上的点数为1或2或3.

故选C.

6．答案：D

解析：“两次均击中”的事件与“至少有一次击中”的事件不互斥，不对立，A不是；“恰有一次击中” 的事件与“至少有一次击中”的事件不互斥，不对立，B不是；“第一次击中”的事件与“至少有一次击中”的事件不互斥，不对立，C不是；“两次均未击中”的事件与“至少有一次击中”的事件不可能同时发生，依题意，它们必有一个发生，

即“两次均未击中”的事件与“至少有一次击中”的事件互为对立事件，D是．

故选D.

7．答案：抛掷一枚质地均匀的骰子两次，向上点数之和为8

解析：抛掷一枚质地均匀的骰子两次， 事件M＝{(2，6)，(3，5)，(4，4)，(5，3)，(6，2)}，

归纳可知，事件M的含义是：抛掷一枚质地均匀的骰子两次，向上点数之和为8的事件．

8．答案：{(正，正)}

解析：同时抛掷两枚质地均匀的硬币，所有可能的结果为(正，正)，(正，反)，(反，正)，(反，反)，

其中事件{(正，正)}，{(反，正)}，{(反，反)}与事件A都不可能同时发生，

所以事件A的一个互斥事件可以是{(正，正)}．

关键能力综合练

1．答案：C

解析：两个小孩的所有结果是：男男，男女，女男，女女，

则所有样本空间为{(男，男)，(男，女)，(女，男)，(女，女)}．

故选C.

2．答案：A

解析：若事件A与事件B是对立事件，则事件A与事件B一定是互斥事件；

若事件A与事件B是互斥事件，不一定得到事件A与事件B对立，

故命题“事件A与事件B对立”是命题“事件A与事件B互斥”的充分不必要条件．

故选A.

3．答案：B

解析：射手进行射击时，事件A1＝“脱靶”，A2＝“中靶”，A3＝“中靶环数大于4”，

事件A1与A2不可能同时发生，并且必有一个发生，即事件A1与A2是互斥且对立，A不是；

事件A1与A3不可能同时发生，但可以同时不发生，即事件A1与A3是互斥不对立，B是；

事件A2与A3可以同时发生，即事件A2与A3不互斥不对立，C不是，显然D不正确．

故选B.

4．答案：D

解析：“恰有一枚炮弹击中飞机”指第一枚击中第二枚没中或第一枚没中第二枚击中，“至少有一枚炮弹击中”包含两种情况：恰有一枚炮弹击中，两枚炮弹都击中．故A⊆D，A∪C＝D，B，D为互斥事件，B∩D＝∅；

A∪B＝“两个炮弹都击中或者都没击中”，B∪D为必然事件，这两者不相等．

故选D.

5．答案：ABD

解析：事件“取出的3支笔中，至少2支一等品”包括2支一等品和1支二等品，3支一等品两种结果，与事件“取出1支一等品和2支二等品”不能同时发生，它们是互斥事件，故A正确；

事件“取出的3支笔中，至多1支二等品”包括2支一等品和1支二等品，3支一等品两种结果，与事件“取出1支一等品和2支二等品”不能同时发生，它们是互斥事件，故B正确；

事件“取出的3支笔中，既有一等品也有二等品”包括1支一等品和2支二等品，2支一等品和1支二等品两种结果，与事件“取出1支一等品和2支二等品”可能同时发生，它们不是互斥事件，故C不正确；

事件“取出的3支笔中，没有二等品”指3支一等品，与事件“取出1支一等品和2支二等品”不能同时发生，它们是互斥事件，故D正确．

故选ABD.

6．答案：BD

解析：6张卡片中一次取出2张卡片的所有情况有：“2张都为红色”“2 张都为绿色”“2张都为蓝色”“1张为红色1张为绿色”“1张为红色1张为蓝色”“1张为绿色1张为蓝色”，选项中给出的四个事件中与“2张都为红色”互斥而非对立的是“2张恰有一张红色”“2张都为绿色”，其中“2张至少一张为红色”包含事件是“2张都为红色”二者并非互斥，与“2张不全为红色”是对立事件．

故选BD.

7．答案：4

解析：长度为2，4，5，7，9的五条线段中任取三条，

则取出的三条线段可以构成一个三角形的基本事件空间是：(2，4，5)，(4，5，7)，(4，7，9)，(5，7，9)，

所以事件A包含的样本点个数为4个．

8．答案：3件至多有2件一级品

解析：“3件都是一级品”为事件A，则A的对立事件为“3件不都是一级品”，

即为“3件至多有2件一级品”．

9．解析：(1)由题意可知3个球可能颜色一样，可能有2个一样，另1个异色，或者三个球都异色．则试验的样本空间

Ω＝{(红，红，红)，(黄，黄，黄)，(蓝，蓝，蓝)，(红，红，黄)，(红，红，蓝)，(蓝，蓝，红)，(蓝，蓝，黄)，(黄，黄，红)，(黄，黄，蓝)，(红，黄，蓝)}．

(2)A＝{(红，黄，蓝)}，

B＝{(红，红，黄)，(红，红，蓝)，(蓝，蓝，红)，(蓝，蓝，黄)，(黄，黄，红)，(黄，黄，蓝)，(红，黄，蓝)}，

C＝{(红，红，黄)，(红，红，蓝)，(蓝，蓝，红)，(蓝，蓝，黄)，(黄，黄，红)，(黄，黄，蓝)}．

D＝{(红，红，红)，(黄，黄，黄)，(蓝，蓝，蓝)}．

(3)由(2)可知事件B包含事件C，事件A和B的交事件与事件D互斥．

10．解析：(1)因为“恰有1名男生”与“恰有2名男生”不可能同时发生，所以它们是互斥事件；当恰有2名女生时它们都不发生，所以它们不是对立事件．

(2)因为“恰有2名男生”时“至少有1名男生”与“全是男生”同时发生，所以它们不是互斥事件．

(3)因为“至少有1名男生”与“全是女生”不可能同时发生，所以它们互斥；由于它们必有一个发生，所以它们是对立事件．

(4)由于选出的是1名男生1名女生时“至少有1名男生”与“至少有1名女生”同时发生，所以它们不是互斥事件．

核心素养升级练

1．答案：B

解析：事件：“至少有一个白球”与事件：“都是红球”不能同时发生，但是对立，故A错误；事件：“恰好有一个白球”与事件：“都是红球”不能同时发生，但从口袋内任取两个球时还有可能是两个都是白球，所以两个事件互斥而不对立，故B正确；事件：“至少有一个白球”与事件：“都是白球”可以同时发生，所以这两个事件不是互斥的，故C错误；事件：“至少有一个白球”与事件：“至少一个红球”可以同时发生，即“一个白球，一个红球” ，所以这两个事件不是互斥的，故D错误．

故选B.

2．答案：电路工作正常　电路工作不正常

3．解析：(1)∵A＝{出现奇数点}＝{1，3，5}，B＝{出现偶数点}＝{2，4，6}，C＝{出现点数小于3}＝{1，2}，

∴A∩B＝∅，B∩C＝{2}．

(2)∵A＝{出现奇数点}＝{1，3，5}，B＝{出现偶数点}＝{2，4，6}，C＝{出现点数小于3}＝{1，2}，

∴A∪B＝{1，2，3，4，5，6}，B∪C＝{1，2，4，6}．

(3)∵A＝{出现奇数点}＝{1，3，5}，B＝{出现偶数点}＝{2，4，6}，C＝{出现点数小于3}＝{1，2}，D＝{出现点数大于2}＝{3，4，5，6}，E＝{出现点数是3的倍数}＝{3，6}．

∴＝{2，4，6}，＝{1，3，5}，＝{1，2，4，5}，

∴＝{1，2}，∩C＝{2}，∪C＝{1，2，3，5}，∪＝{1，2，4，5}．