【同步练习】高中数学人教A版(2019)必修第二册--10.1.4概率的基本性质 课时作业（含解析）

这是一份【同步练习】高中数学人教A版(2019)必修第二册--10.1.4概率的基本性质 课时作业（含解析），共8页。试卷主要包含了1.4　概率的基本性质等内容，欢迎下载使用。
10．1.4　概率的基本性质必备知识基础练　1．已知随机事件A，B，C中，A与B互斥，B与C对立，且P(A)＝0.3，P(C)＝0.6，则P(A＋B)＝(　　)A．0.3    B．0.6C．0.7    D．0.82．围棋盒子中有多粒黑子和白子，已知从中取出2粒都是黑子的概率为，都是白子的概率是，则从中任意取出2粒恰好是同一色的概率是(　　)A．    B．C．    D．13．某射手的一次射击中，射中10环，9环，8环的概率分别为0.2，0.3，0.1.则此射手在一次射击中不够8环的概率为(　　)A．0.4    B．0.3C．0.6    D．0.94．人类通常有O，A，B，AB四种血型，某一血型的人能给哪些血型的人输血，是有严格规定的，输血法则可归结为4条：①X→X；②O→X；X→AB；④不满足上述3条法则的任何关系式都是错误的(其中X代表O，A，B，AB中某种血型，箭头左边表示供血者，右边表示受血者).已知我国O，A，B，AB四种血型的人数所占比例分别为41%，28%，24%，7%，在临床上，按照规则，若受血者为A型血，则一位供血者不能为这位受血者正确输血的概率为(　　)A．0.27    B．0.31C．0.42    D．0.695．抛掷一个质地均匀的骰子的试验，事件A表示“小于5的偶数点出现”，事件B表示“不小于5的点数出现”，则一次试验中，事件A或事件B至少有一个发生的概率为(　　)A．    B．C．    D．6．(多选)甲、乙两人下棋，和棋的概率为，乙获胜的概率为，则下列说法错误的是(　　)A．甲获胜的概率是B．甲不输的概率是C．乙输的概率是D．乙不输的概率是7．中国乒乓球队甲、乙两名运动员参加奥运乒乓球女子单打比赛，甲夺得冠军的概率是，乙夺得冠军的概率是，那么中国队夺得女子乒乓球单打冠军的概率为________．8．从一批羽毛球产品中任取一个，质量小于4.8 g的概率为0.3，质量小于4.85 g的概率为0.32，那么质量在[4.8，4.85)(g)范围内的概率是________． 
关键能力综合练　 1．在所有的两位数(10～99)中，任取一个数，则这个数能被2或3整除的概率是(　　)A．　　　B．　　　C．　　　D．2．从装有3个红球、2个白球的袋中任取3个球，则所取的3个球中至少有1个白球的概率是(　　)A．    B．    C．    D．3．口袋里装有1红，2白，3黄共6个形状相同小球，从中取出2球，事件A＝“取出的两球同色”，事件B＝“取出的2球中至少有一个黄球”，事件C＝“取出的2球至少有一个白球”，事件D＝“取出的2球不同色”，E＝“取出的2球中至多有一个白球”．下列判断中正确的是(　　)A．P(A＋B)＝P(A)＋P(B)B．P(C)＋P(D)＝1C．P(C∪E)＝1D．P(B)＝P(C)4．在5件产品中，有3件一等品和2件二等品，从中任取2件，以为概率的事件是(　　)A．恰有1件一等品    B．至少有一件一等品C．至多有一件一等品    D．都不是一等品5．盘子里有肉馅、素馅和豆沙馅的包子共10个，从中随机取出1个，若是肉馅包子的概率为，不是豆沙馅包子的概率为，则素馅包子的个数为(　　)A．1    B．2    C．3    D．46．(多选)高一(2)班数学兴趣小组有男生和女生各3名，现从中任选2名学生去参加数学竞赛，则(　　)A．恰有一名参赛学生是男生的概率为B．至少有一名参赛学生是男生的概率为C．至多有一名参赛学生是男生的概率为D．两名参赛学生都是男生的概率为7．某次知识竞赛规则如下：主办方预设3个问题，选手能答对这3个问题，即可晋级下一轮．假设某选手回答正确的个数为0，1，2的概率分别是0.1，0.2，0.3，则该选手晋级下一轮的概率为________．8.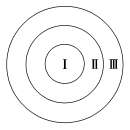如图所示，靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成，射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.35，0.30，0.25，则射手命中圆环Ⅱ或Ⅲ的概率为________，不中靶的概率是________．9．某品牌计算机售后保修期为1年，根据大量的维修记录资料，这种品牌的计算机在使用一年内需要维修1次的占15%，需要维修2次的占6%，需要维修3次的占4%，(1)某人购买了一台这个品牌的计算机，设Ak＝“一年内需要维修k次”，k＝0，1，2，3，请填写下表： 事件A0A1A2A3概率    事件A0，A1，A2，A3是否满足两两互斥？(2)求下列事件的概率：①A＝“在1年内需要维修”；②B＝“在1年内不需要维修”；③C＝“在1年内维修不超过1次” .  10.经统计，在某储蓄所一个营业窗口排队等候的人数及相应概率如下： 排队人数01234≥5概率0.10.160.30.30.10.04(1)至多有2人排队等候的概率是多少？              (2)至少有3人排队等候的概率是多少？              核心素养升级练　 1．(多选)张明与李华两人做游戏，则下列游戏规则中公平的是(　　)A．抛掷一枚质地均匀的骰子，向上的点数为奇数则张明获胜，向上的点数为偶数则李华获胜B．同时抛掷两枚质地均匀的硬币，恰有一枚正面向上则张明获胜，两枚都正面向上则李华获胜C．从一副不含大小王的扑克牌中抽一张，扑克牌是红色的则张明获胜，扑克牌是黑色的则李华获胜D．张明、李华两人各写一个数字6或8，两人写的数字相同则张明获胜，否则李华获胜2．掷一枚骰子的试验中，出现各点的概率均为，事件A表示“小于5的偶数点出现”，事件B表示“小于5的点数出现”，则一次试验中，事件(表示事件B的对立事件)的概率为P()＝________，事件A＋发生的概率为________．3．袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个，从中任取一球，得到红球的概率是，得到黑球或黄球的概率是，得到黄球或绿球的概率也是.(1)试分别求得到黑球、黄球、绿球的概率；(2)从中任取一球，求得到的不是红球也不是绿球的概率．          10．1.4　概率的基本性质必备知识基础练1．答案：C解析：因为P(C)＝0.6，事件B与C对立，所以P(B)＝0.4，又P(A)＝0.3，A与B互斥，所以P(A＋B)＝P(A)＋P(B)＝0.3＋0.4＝0.7.故选C.2．答案：C解析：从中取出2粒恰好是同一色包含都是黑子或都是白子两个事件，这两个事件是互斥事件，设两粒是同一色为事件A，同为黑子为事件B，同为白子为事件C，则P(A)＝P(B＋C)＝P(B)＋P(C)＝＋＝.故选C.3．答案：A解析：因为某射手的一次射击中，射中10环，9环，8环的概率分别为0.2，0.3，0.1.所以在一次射击中不够8环的概率为1－0.2－0.3－0.1＝0.4.故选A.4．答案：B解析：当受血者为A型血时，供血者可以为A型或O型，即B，AB两种血型不能为供血者，我国O，A，B，AB四种血型的人数所占比例分别为41%，28%，24%，7%，所以一位供血者不能为这位受血者正确输血的概率为：P＝24%＋7%＝31%＝0.31.故选B.5．答案：A解析：事件A表示“小于5的偶数点出现”，事件B表示“不小于5的点数出现”，∴P(A)＝＝，P(B)＝＝，又小于5的偶数点有2和4，不小于5的点数有5和6，所以事件A和事件B为互斥事件，则一次试验中，事件A或事件B至少有一个发生的概率为P(A∪B)＝P(A)＋P(B)＝＋＝.故选A.6．答案：BCD解析：“甲获胜”是“和棋或乙获胜”的对立事件，所以“甲获胜”的概率是1－－＝，故A正确；设甲不输为事件A，则事件A是“甲获胜”和“和棋”这两个互斥事件的并事件，所以P(A)＝＋＝，故B错误；“乙输”的概率即“甲获胜”的概率，为，故C错误；设乙不输为事件B，则事件B是“乙获胜”和“和棋”这两个互斥事件的并事件，所以P(B)＝＋＝，故D错误．故选BCD.7．答案：解析：设“甲夺得冠军”为事件A，“乙夺得冠军”为事件B，则P(A)＝，P(B)＝.∵A，B是互斥事件，∴P(A∪B)＝P(A)＋P(B)＝＋＝.8．答案：0.02解析：从羽毛球产品中任取一个，A＝{质量小于4.8 g}，B＝{质量在[4.8，4.85)(g)范围内}，C＝{质量小于4.85 g}，事件A与B互斥，且C＝A＋B，而P(A)＝0.3，P(C)＝0.32，由P(C)＝P(A＋B)＝P(A)＋P(B)，得P(B)＝P(C)－P(A)＝0.32－0.3＝0.02，所以质量在[4.8，4.85)(g)范围内的概率是0.02.关键能力综合练1．答案：C解析：所有的两位数(10～99)共有90个，其中被2整除的有10，12，14，…，98，共计45个．被3整除的有12，15，18，…，99，共计30个，被6整除的有12，18，24，…，96，共计15个，故能被2或3整除的数有45＋30－15＝60个．任取一个数，则这个数能被2或3整除的概率为＝.故选C.2．答案：D解析：记3个红球分别为a1，a2，a3，2个白球分别为b1，b2，从3个红球、2个白球中任取3个，则样本空间Ω＝{(a1，a2，a3)，(a1，a2，b1)，(a1，a2，b2)，(a1，a3，b1)，(a1，a3，b2)，(a2，a3，b1)，(a2，a3，b2)，(a1，b1，b2)，(a2，b1，b2)，(a3，b1，b2)}，共含10个样本点，样本点出现的机会均等，因此这些样本点的出现是等可能的．用事件A表示“所取的3个球中至少有1个白球”，则其对立事件表示“所取的3个球中没有白球”，则事件包含的样本点有1个(a1，a2，a3)，所以P()＝.故P(A)＝1－P()＝1－＝.故选D.3．答案：C解析：依题意，P(A)＝，P(B)＝1－＝，P(A)＋P(B)＝>1，而P(A＋B)≤1，A不正确；P(C)＝1－＝，P(D)＝1－P(A)＝，P(C)＋P(D)>1，B不正确；事件C是含有1个白球与含有两个白球的两个互斥事件和，事件E是含有1个白球与没有白球的两个互斥事件和，事件C∪E是必然事件，因此P(C∪E)＝1，C正确；因P(B)＝，P(C)＝，则P(B)≠P(C)，即D不正确．故选C.4．答案：C解析：将3件一等品编号为1，2，3，2件二等品编号为4，5，从中任取2件有10种取法：(1，2)，(1，3)，(1，4)，(1，5)，(2，3)，(2，4)，(2，5)，(3，4)，(3，5)，(4，5).其中恰含有1件一等品的取法有：(1，4)，(1，5)，(2，4)，(2，5)，(3，4)，(3，5)，恰有1件一等品的概率为P1＝，恰有2件一等品的取法有：(1，2)，(1，3)，(2，3).故恰有2件一等品的概率为P2＝，其对立事件是“至多有一件一等品”，概率为P3＝1－P2＝1－＝.故选C.5．答案：C解析：由题意可知，肉馅包子的个数为10×＝4，从中随机取出1个，不是豆沙馅包子的概率为，则该包子是豆沙馅包子的概率为1－＝，所以，豆沙馅包子的个数为10×＝3，因此，素馅包子的个数为10－4－3＝3.故选C.6．答案：AC解析：从数学兴趣小组的6名学生中任选2名学生去参加数学竞赛，共有15种等可能的结果．恰有一名参赛学生是男生，即从3名男生中任选1人，从3名女生中任选1人，有3×3＝9(种)结果，所以恰有一名参赛学生是男生的概率为＝，A对；“至少有一名参赛学生是男生”的对立事件为“两名参赛学生都是女生”，从3名女生中任选2人有3种结果，所以至少有一名参赛学生是男生的概率为1－＝，B错；“两名参赛学生都是男生”，从3名男生中任选2人有3种结果，其概率为＝，D错；“至多有一名参赛学生是男生”的对立事件为“两名参赛学生都是男生”，所以至多有一名参赛学生是男生的概率为1－＝，C对．故选AC.7．答案：0.4解析：记“答对0个问题”为事件A，“答对1个问题”为事件B，“答对2个问题”为事件C，“答对3个问题(即晋级下一轮)”为事件D，则“不能晋级下一轮”为事件D的对立事件，且＝A∪B∪C.显然P()＝P(A)＋P(B)＋P(C)＝0.1＋0.2＋0.3＝0.6.故P(D)＝1－P()＝1－0.6＝0.4.8．答案：0.55　0.10解析：设射手命中圆面Ⅰ为事件A，命中圆环Ⅱ为事件B，命中圆环Ⅲ为事件C，不中靶为事件D，则P(A)＝0.35，P(B)＝0.30，P(C)＝0.25，A，B，C两两互斥，故射手命中圆环Ⅱ或Ⅲ的概率为P(B∪C)＝P(B)＋P(C)＝0.30＋0.25＝0.55，射手中靶的概率为P(A∪B∪C)＝P(A)＋P(B)＋P(C)＝0.35＋0.30＋0.25＝0.90.因为中靶和不中靶是对立事件，所以不中靶的概率P(D)＝1－P(A∪B∪C)＝1－0.90＝0.10.9．解析：(1)因为一年内需要维修1次的占15%，需要维修2次的占6%，需要维修3次的占4%，则有P(A1)＝0.15，P(A2)＝0.06，P(A3)＝0.04，显然事件A0，A1，A2，A3中，任意两个不可能同时发生，因此事件A0，A1，A2，A3两两互斥，于是得P(A0)＝1－(0.15＋0.06＋0.04)＝0.75，填表如下： 事件A0A1A2A3概率0.750.150.060.04所以事件A0，A1，A2，A3满足两两互斥．(2)①由(1)知，“在1年内需要维修”的事件，即事件A1，A2，A3至少有一个发生，而它们两两互斥，所以P(A)＝P(A1∪A2∪A3)＝P(A1)＋P(A2)＋P(A3)＝0.25.②“在1年内不需要维修”的事件，即事件A0发生，所以P(B)＝P(A0)＝0.75.③“在1年内维修不超过1次”的事件，即事件A0，A1至少发生一个，所以P(C)＝P(A0∪A1)＝P(A0)＋P(A1)＝0.9.10．解析：记“无人排队等候”为事件A，“1人排队等候”为事件B，“2人排队等候”为事件C，“3人排队等候”为事件D，“4人排队等候”为事件E，“5人及5人以上排队等候”为事件F，则事件A，B，C，D，E，F互斥．(1)记“至多2人排队等候”为事件G，则G＝A∪B∪C，所以P(G)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2) 记“至少3人排队等候”为事件H，则H＝D∪E∪F，所以P(H)＝P(D)＋P(E)＋P(F)＝0.3＋0.1＋0.04＝0.44. 核心素养升级练1．答案：ACD解析：选项A中，向上的点数为奇数与向上的点数为偶数的概率相等，A符合题意；选项B中，张明获胜的概率是，而李华获胜的概率是，故游戏规则不公平，B不符合题意；选项C中，扑克牌是红色与扑克牌是黑色的概率相等，C符合题意；选项D中，两人写的数字相同与两人写的数字不同的概率相等，D符合题意．故选ACD.2．答案：　解析：由题意知，表示“大于或等于5的点数出现”，则P()＝＝.事件A与事件互斥，由概率的加法公式得P(A＋)＝P(A)＋P()＝＋＝＝.3．解析：(1)从袋中任取一球，记事件“得到红球”“得到黑球”“得到黄球”“得到绿球”分别为A，B，C，D，则P(A)＝，P(B∪C)＝P(B)＋P(C)＝，P(C∪D)＝P(C)＋P(D)＝，P(B∪C∪D)＝P(B)＋P(C)＋P(D)＝1－P(A)＝1－＝.联立解得P(B)＝，P(C)＝，P(D)＝，故得到黑球，得到黄球，得到绿球的概率分别为，，.(2)事件“得到红球或绿球”可表示为事件A∪D，由(1)及互斥事件的概率加法公式得P(A∪D)＝P(A)＋P(D)＝＋＝，故得到的不是红球也不是绿球的概率P＝1－P(A∪D)＝1－＝.