


【同步练习】高中数学人教A版(2019)必修第二册--6.2.1 向量的加法运算 同步练习(含解析)
展开6.2.1 向量的加法运算(同步练习)
一、选择题
1.下列等式错误的是( )
A.![]() 0=0+
0=0+![]() =
=![]() B.++=0
B.++=0
C.+=0 D.+=++
2.如图,四边形ABCD是梯形,AD∥BC,对角线AC与BD相交于点O,则+++等于( )
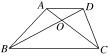
A. B. C. D.
3.下列说法正确的个数为( )
①如果非零向量a与b的方向相同或相反,那么a+b的方向必与a或b的方向相同;
②在△ABC中,必有++=0;
③若++=0,则A,B,C一定为一个三角形的三个顶点;
④若a,b均为非零向量,则|a+b|=|a|+|b|.
A.0 B.1
C.2 D.3
4.如图所示,在四边形ABCD中,=+,则四边形为( )
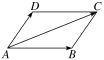
A.矩形 B.正方形 C.平行四边形 D.菱形
5.在矩形ABCD中,||=4,||=2,则向量++的长度为( )
A.2 B.4
C.12 D.6
6.若在△ABC中,=a,=b,且|a|=|b|=1,|a+b|=,则△ABC的形状是( )
A.正三角形 B.锐角三角形
C.斜三角形 D.等腰直角三角形
7.如图所示的方格纸中有定点O,P,Q,E,F,G,H,则+=( )
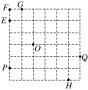
A. B. C. D.
8.(多选)对于任意一个四边形ABCD,下列式子能化简为的是( )
A.+ B.++
C.++ D.++
二、填空题
9.如图,在平行四边形ABCD中,O是AC和BD的交点.
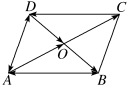
(1)++=________;(2)++=________
10.已知在菱形ABCD中,∠DAB=60°,||=1,则|+|=________
11.如图所示,若P为△ABC的外心,且+=,则∠ACB=________
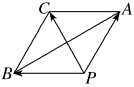
12.如图,已知在矩形ABCD中,||=4,设=a,=b,=c,则|a+b+c|=________
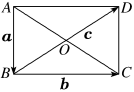
13.设非零向量a,b,c,若p=++,则|p|的取值范围为________
三、解答题
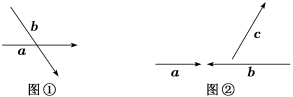
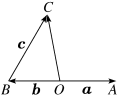
14.如图①②,已知向量a,b,c,求作向量a+b和a+b+c.
15.在四边形ABCD中,对角线AC,BD交于点O且||=||=1,+=+=0,cos∠DAB=. 求|+|与|+|的值.
16.如图,O为正六边形ABCDEF的中心,根据图示计算:
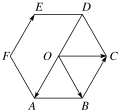
(1)+;(2)+;(3)+.
17.在静水中船的速度为20 m/min,水流的速度为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸.
(1)求船行进的方向;(2)经过3小时,该船的实际航程是多少km?
参考答案及详细解析:
1.B解析:由向量加法可知++=+=2.
2.B 解析:+++=+++=++=+=.
3.B 解析:①错,若a+b=0,则a+b的方向是任意的;②正确;③错,当A,B,C三点共线时,也满足++=0;④错,|a+b|≤|a|+|b|.
4.C 解析:∵=+4,∴=+=++=++=,即=,∴AB=DC,AB∥DC,∴四边形ABCD为平行四边形.
5.B 解析:因为+=,所以++的长度为的模的2倍.
又||==2,所以向量++的长度为4.
6.D 解析:由于||=|a|=1,||=|b|=1,||=|a+b|=,所以△ABC为等腰直角三角形,故选D.
7.C 解析:+=.
8.ABD 解析:在A中,+=;在B中,++=+=;在C中,++=+=;在D中,++=+=+=.
二、填空题
9.答案:(1) (2)0
解析:(1)++=+=; (2)++=++=+=0.
10.答案:1
解析:在△ABD中,AD=AB=1,∠DAB=60°,则BD=1,所以|+|=||=1.
11.答案:120°
解析:因为P为△ABC的外心,所以PA=PB=PC,因为+=,由向量的线性运算可得四边形PACB是菱形,且∠PAC=60°,所以∠ACB=120°.
12.答案:8
解析:因为a+b+c=++=+,
延长BC至E,使CE=BC,连接DE(图略).
由于==,所以四边形ACED是平行四边形,所以=,
所以+=+=,所以|a+b+c|=||=2||=2||=8.
13.答案:[0,3]
解析:因为,,是三个单位向量,因此当三个向量同向时,|p|取最大值3.当三个向量两两成120°角时,它们的和为0,故|p|的最小值为0.
三、解答题
14.解:(1)在平面内任意取一点O,作=a,=b,则=a+b.
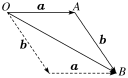
(2)在平面内任意取一点O,作=a,=b,=c,则=a+b+c.
15.解:∵+=+=0,∴=,=.∴四边形ABCD是平行四边形.
又||=||=1,∴四边形ABCD为菱形.
又cos∠DAB=,0°<∠DAB<180°,∴∠DAB=60°,∴△ABD为正三角形.
∴|+|=|+|=||=2||=,|+|=||=||=1.
16.解:(1)因为四边形OABC是以OA,OC为邻边的平行四边形,OB为其对角线,所以+=.
(2)因为与方向相同且长度相等,所以与是相等向量,故+与方向相同,长度为长度的2倍,因此+可用表示.所以+=-.
(3)因为与长度相等且方向相反,所以+=0.
17.解:(1)作出图形如图所示.船速v船与岸的方向成α角,由图可知v水+v船=v实际,
结合已知条件,四边形ABCD为平行四边形,
在Rt△ACD中,||=||=|v水|=10 m/min,||=|v船|=20 m/min,
∴cos α===,∴α=60°,从而船与水流方向成120°的角.
故船行进的方向是与水流的方向成120°的角的方向.
(2)由图可知||=||=×20=10(m/min)=(km/h),
故经过3小时,该船的实际航程是3×=(km).
高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算当堂达标检测题: 这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算当堂达标检测题,共4页。试卷主要包含了2 平面向量的运算等内容,欢迎下载使用。
【同步练习】高中数学人教A版(2019)必修第二册--6.2.2向量的减法运算 课时作业(含解析): 这是一份【同步练习】高中数学人教A版(2019)必修第二册--6.2.2向量的减法运算 课时作业(含解析),共8页。试卷主要包含了化简等内容,欢迎下载使用。
人教A版 (2019)必修 第二册6.2 平面向量的运算测试题: 这是一份人教A版 (2019)必修 第二册6.2 平面向量的运算测试题,共2页。试卷主要包含了已知有向线段不平行,则,设是平面内任意三点,计算,给出下面四个结论等内容,欢迎下载使用。













