【同步练习】高中数学人教A版(2019)必修第二册--6.2.3向量的数乘运算 课时作业（含解析）

6．2.3　向量的数乘运算

必备知识基础练　

1．(2a－b)－(2a＋b)＝(　　)

A．a－2b    B．－2b

C．0    D．b－a

2．已知a＝2e，b＝－3e，c＝6e，则3a－2b＋c＝(　　)

A．18e    B．－3e

C．20e    D．－18e

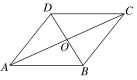
3．平行四边形ABCD的对角线的交点为O，则＋＝(　　)

A．2    B．2

C．2    D．2

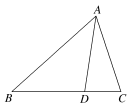
4．若AD是△ABC的中线，已知＝a，＝b，则＝(　　)

A．－(a＋b)    B．(a＋b)

C．(－a＋b)    D．(a－b)

5．点C在线段AB上，且||＝||，若＝λ，则λ＝(　　)

A．    B．－

C．    D．－

6．化简：(2a－b)－3(a＋b)＋2(a－2b)＝________．

7．已知＝－，则使得＝λ的实数λ＝________.

8．判断向量a，b是否共线(其中e1，e2是两个非零不共线的向量)：

(1)a＝3e1，b＝－9e1；

(2)a＝e1－e2，b＝3e1－2e2；

(3)a＝e1－e2，b＝3e1＋3e2.

关键能力综合练　

1．(多选)在△ABC中，＝2，则＝(　　)

A．＋    B．－C．＋    D．＋

2．设a，b是两个不共线的向量，若向量m＝a＋kb(k∈R)与向量n＝2a－b共线，则(　　)

A．k＝－    B．k＝0C．k＝    D．k＝1

3.

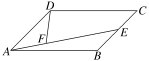
如图，在平行四边形ABCD中，E是BC的中点，＝3，则＝(　　)

A．－＋    B．－C．－    D．－

4．已知向量a与b不共线，且＝a＋mb(m≠1)，＝na＋b.若A、B、C三点共线，则实数m，n满足的条件为(　　)

A．m＋n＝1    B．m＋n＝－1C．mn＝1    D．mn＝－1

5．已知＝a＋5b，＝－2a＋8b，＝2a＋10b，则共线的三点为(　　)

A．B，C，D    B．A，B，CC．A，C，D    D．A，B，D

6．设D为△ABC所在平面内一点，＝2，E为BC的中点，则＝(　　)

A．＋    B．＋

C．－    D．－

7．已知＝，＝λ，则实数λ＝________.

8．设a，b是两个不共线的非零向量，若向量ka＋2b与8a＋kb的方向相反，则k＝________．

9．在平行四边形ABCD中，＝，＝，设＝a，＝b.

(1)用a，b表示；

(2)用a，b表示.

10．两个非零向量a，b不共线．

(1)若＝a＋b，＝2a＋8b，＝3(a－b)，求证：A、B、D三点共线；

(2)求实数k使ka＋b与2a＋kb共线．

核心素养升级练　

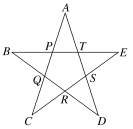
1.2021年是中国共产党建党100周年，“红星闪闪放光彩”，国旗和国徽上的五角星是革命和光明的象征．正五角星是一个非常优美的几何图形，且与黄金分割有着紧密联系，在如图所示的五角星中，以A、B、C、D、E为顶点的多边形为正五边形，且＝，设－＝λ，则λ＝(　　)

A．    B．C．－    D．

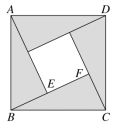
2.我国古代人民早在几千年以前就已经发现并应用勾股定理了，勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的，被后人称为“赵爽弦图”．“赵爽弦图”是数形结合思想的体现，是中国古代数学的图腾，还被用作第24届国际数学家大会的会徽．如图，大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的，若＝a，＝b，E为BF的中点，则＝(　　)

A．a＋b    B．a＋b

C．a＋b    D．a＋b

3．若点G为△ABC的重心．

(1)化简：＋＋；

(2)求证：＝(＋＋).

6．2.3　向量的数乘运算

必备知识基础练

1．答案：B

解析：(2a－b)－(2a＋b)＝2a－2a－b－b＝－2b，故选B.

2．答案：A

解析：3a－2b＋c＝3×2e－2×(－3e)＋6e＝18e.故选A.

3．答案：C

解析：根据向量的平行四边形法则可得＋＝＝2.故选C.

4．答案：D

解析：因为D是BC的中点，由向量的平行四边形法则可得：＝(＋)＝(a－b)，故选D.

5．答案：D

解析：不妨设||＝4a，则||＝||＝3a，因为点C在线段AB上，则＝－，故选D.

6．答案：2a－b

解析：(2a－b)－3(a＋b)＋2(a－2b)＝a－b－a－3b＋2a－4b＝2a－b.

7．答案：－2

解析：＝－，则A在线段BC上，且AC＝2AB，所以＝－2，又＝λ，所以λ＝－2.

8．解析：(1)因a＝3e1，b＝－9e1，则有b＝－3a，所以a，b共线．

(2)因a＝e1－e2，b＝3e1－2e2＝6(e1－e2)，则b＝6a，所以a，b共线．

(3)假设b＝λa(λ∈R)，则3e1＋3e2＝λ(e1－e2)，即(3－λ)e1＋(3＋λ)e2＝0，

因e1，e2不共线，于是得，此方程组无解，因此不存在实数λ，使得b＝λa，

所以a，b不共线．

关键能力综合练

1．答案：ABD

解析：＝－＝＋＝＋(＋)＝＋.故选ABD.

2．答案：A

解析：∵a，b是两个不共线的向量，且m∥n，故存在实数λ，使得m＝λn⇒a＋kb＝2λa－λb⇒⇒k＝－.故选A.

3．答案：C

解析：＝－＝－＝(＋)－＝－.故选C.

4．答案：C

解析：若A、B、C三点共线，则∥，则＝λ，即a＋mb＝nλ·a＋λb，∵a与b不共线，∴⇒mn＝1.故选C.

5．答案：D

解析：∵＝－2a＋8b，＝2a＋10b不满足共线定理，A错误；∵＝a＋5b，＝－2a＋8b不满足共线定理，B错误；∵＝＋＝a＋5b－2a＋8b＝－a＋13b，＝＋＝a＋5b＋2a＋10b＝3a＋15b，∴，不满足共线定理，C错误；∵＝a＋5b＝(2a＋10b)＝，D正确．

6．答案：A

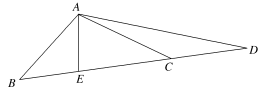
解析：因为＝2，E为BC的中点，所以＝＋＝＋＝＋(－)＝＋，故选A.

7．答案：－3

解析：由题，因为＝－，所以＝＝(－)，即＝－3，所以λ＝－3.

8．答案：－4

解析：由题意知，ka＋2b＝λ(8a＋kb)(λ<0).∴(k－8λ)a＋(2－λk)·b＝0，又a，b不共线，∴⇒λ＝－，k＝－4.

9．解析：(1)∵＝，且四边形ABCD是平行四边形，

∴＝＋＝＋＝＋＝a＋b.

(2)∵＝，

∴＝－＝－＝(－)－＝－－＝－a－b.

10．解析：(1)证明：因为＝a＋b，＝2a＋8b，＝3(a－b)，

所以＝＋＝2a＋8b＋3(a－b)＝5a＋5b，则＝5，

所以，共线，两个向量有公共点B，

所以A、B、D三点共线．

(2)若ka＋b与2a＋kb共线，则存在实数μ，使得ka＋b＝μ(2a＋kb)＝2μa＋kμb，

所以⇒1＝2μ2⇒μ＝±，

所以k＝2μ＝±.

核心素养升级练

1．答案：D

解析：五角星中，＝，＝，则－＝－＝＋＝，由于＝⇒＝＝＝－＝，则λ＝，故选D.

2．答案：A

解析：＝＋＝＋＋＝＋－＝＋－(＋)，即＝＋－(＋)，∴＝a＋b⇒＝a＋b.故选A.

3．解析：

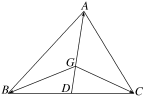
(1)延长AG交BC于D，如图，

因点G为△ABC的重心，则D是BC边中点，并且有||＝2||，即＝2，

又GD是△GBC的中线，则有2＝＋，于是得＝＋，

所以＋＋＝0.

(2)证明：由(1)知：＋＋＝0，取△ABC所在平面内任意一点O，

则有(－)＋(－)＋(－)＝0，

即(＋＋)－3＝0，

亦即3＝＋＋，

所以＝(＋＋).