


所属成套资源:【练习+测试】高中数学人教A版(2019)必修第二册 课时作业+单元测试(含解析)
【同步练习】高中数学人教A版(2019)必修第二册--8.5.3平面与平面平行 同步练习(含答案)
展开
这是一份【同步练习】高中数学人教A版(2019)必修第二册--8.5.3平面与平面平行 同步练习(含答案),共6页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
![]() 8.5.3 平面与平面平行一、单选题1.在棱长为1的正方体
8.5.3 平面与平面平行一、单选题1.在棱长为1的正方体![]() 中,
中,![]() 分别为
分别为![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面
的平面![]() //平面
//平面![]() ,则平面
,则平面![]() 截该正方体所得截面为( )A.三角形 B.五边形 C.平行四边形 D.等腰梯形2.已知直线l,m,平面α,β,γ,则下列条件能推出l∥m的是( )A.l⊂α,m⊂β,α∥β B.α∥β,α∩γ=l,β∩γ=mC.l∥α,m⊂α D.l⊂α,α∩β=m3.平面α∥平面β,直线l∥α,则( )A.l∥β B.l⊂βC.l∥β或l⊂β D.l,β相交4.已知正方体
截该正方体所得截面为( )A.三角形 B.五边形 C.平行四边形 D.等腰梯形2.已知直线l,m,平面α,β,γ,则下列条件能推出l∥m的是( )A.l⊂α,m⊂β,α∥β B.α∥β,α∩γ=l,β∩γ=mC.l∥α,m⊂α D.l⊂α,α∩β=m3.平面α∥平面β,直线l∥α,则( )A.l∥β B.l⊂βC.l∥β或l⊂β D.l,β相交4.已知正方体![]() 的体积为1,点
的体积为1,点![]() 在线段
在线段![]() 上(点
上(点![]() 异于
异于![]() 两点),点
两点),点![]() 在
在![]() 上满足
上满足![]() ,若平面
,若平面![]() 截正方体
截正方体![]() 所得的截面为五边形,则线段
所得的截面为五边形,则线段![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.平面
5.平面![]() 过正方体的顶点A,
过正方体的顶点A,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() 与
与![]() 所成角的大小为( )A.
所成角的大小为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.在棱长为2的正方体
6.在棱长为2的正方体![]() 中,E为棱BC的中点,F是侧面
中,E为棱BC的中点,F是侧面![]() 内的动点,若
内的动点,若![]() 平面
平面![]() ,则点F轨迹的长度为( )A.
,则点F轨迹的长度为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.在棱长为3的正方体
7.在棱长为3的正方体![]() 中,点Р是侧面
中,点Р是侧面![]() 上的点,且点Р到棱
上的点,且点Р到棱![]() 与到棱AD的距离均为1,用过点Р且与
与到棱AD的距离均为1,用过点Р且与![]() 垂直的平面去截该正方体,则截面在正方体底面ABCD的投影多边形的面积是( )A.
垂直的平面去截该正方体,则截面在正方体底面ABCD的投影多边形的面积是( )A.![]() B.5 C.
B.5 C.![]() D.88.对于不重合的两个平面
D.88.对于不重合的两个平面![]() 与
与![]() ,给定下列条件:①存在平面
,给定下列条件:①存在平面![]() ,使得
,使得![]() ,
,![]() 都垂直于
都垂直于![]() ;②存在平面
;②存在平面![]() ,使得
,使得![]() ,
,![]() 都平行于
都平行于![]() ;③存在直线
;③存在直线![]() ,直线
,直线![]() ,使得
,使得![]() ;④存在异面直线
;④存在异面直线![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() .其中,可以判定
.其中,可以判定![]() 与
与![]() 平行的条件有( )A.1个 B.2个 C.3个 D.4个二、多选题9.已知a,b是两条不重合的直线,
平行的条件有( )A.1个 B.2个 C.3个 D.4个二、多选题9.已知a,b是两条不重合的直线,![]() 、
、![]() 是两个不重合的平面,则下列说法中正确的是( )A.若
是两个不重合的平面,则下列说法中正确的是( )A.若![]() ,
,![]() ,则
,则![]() 与
与![]() 一定相交B.若
一定相交B.若![]() ,
,![]() ,则
,则![]() C.若
C.若![]() ,
,![]() ,则直线a平行于平面
,则直线a平行于平面![]() 内的无数条直线D.若
内的无数条直线D.若![]() ,
,![]() ,
,![]() ,则a与b是异面直线10.已知正方体
,则a与b是异面直线10.已知正方体![]() 的外接球表面积为
的外接球表面积为![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() ,
,![]() 上,且
上,且![]() 四点共面,则( ).A.
四点共面,则( ).A.![]() B.若四边形
B.若四边形![]() 为菱形,则其面积的最大值为
为菱形,则其面积的最大值为![]() C.四边形
C.四边形![]() 在平面
在平面![]() 与平面
与平面![]() 内的正投影面积之和的最大值为6D.四边形
内的正投影面积之和的最大值为6D.四边形![]() 在平面
在平面![]() 与平面
与平面![]() 内的正投影面积之积的最大值为411.下面四个命题中正确的有( )A.在空间中,若两条直线不相交,则它们一定平行B.平行于同一个平面的两个平面平行C.如果一条直线和两条平行直线中的一条相交,那么它也和另一条相交D.已知空间四条直线
内的正投影面积之积的最大值为411.下面四个命题中正确的有( )A.在空间中,若两条直线不相交,则它们一定平行B.平行于同一个平面的两个平面平行C.如果一条直线和两条平行直线中的一条相交,那么它也和另一条相交D.已知空间四条直线![]() ,如果
,如果![]() ,且
,且![]() ,那么
,那么![]() 12.已知
12.已知![]() ,
,![]() 表示两条不重合的直线,
表示两条不重合的直线,![]() ,
,![]() ,
,![]() 表示三个不重合的平面,给出下列命题,其中正确的是( )A.若
表示三个不重合的平面,给出下列命题,其中正确的是( )A.若![]() ,
,![]() ,且
,且![]() ,则
,则![]() B.若
B.若![]() ,
,![]() 相交且都在
相交且都在![]() ,
,![]() 外,
外,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() C.若
C.若![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,
,![]() ,则
,则![]() 三、填空题13.如图所示的是正方体的平面展开图.有下列四个命题:①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.其中,正确命题的序号是________.
三、填空题13.如图所示的是正方体的平面展开图.有下列四个命题:①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.其中,正确命题的序号是________.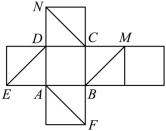 14.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α、β都垂直于γ;②存在平面γ,使α、β都平行于γ;③α内有不共线的三点到β的距离相等;④存在异面直线l,m,使得l
14.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α、β都垂直于γ;②存在平面γ,使α、β都平行于γ;③α内有不共线的三点到β的距离相等;④存在异面直线l,m,使得l![]() α,l
α,l![]() β,m
β,m![]() α,m
α,m![]() β..其中可以判断两个平面α与β平行的条件有___个.15.若平面
β..其中可以判断两个平面α与β平行的条件有___个.15.若平面![]() ∥平面
∥平面![]() ,
,![]() ,下列说法正确的是_____.(填序号) ①a与β内任一直线平行;②a与β内无数条直线平行;③a与β内任一直线不垂直;④a与β无公共点.16.如图,正三棱柱
,下列说法正确的是_____.(填序号) ①a与β内任一直线平行;②a与β内无数条直线平行;③a与β内任一直线不垂直;④a与β无公共点.16.如图,正三棱柱![]() 的底面边长是2,侧棱长是
的底面边长是2,侧棱长是![]() ,M为
,M为![]() 的中点,N是侧面
的中点,N是侧面![]() 上一点,且
上一点,且![]() ∥平面
∥平面![]() ,则线段MN的最大值为________.
,则线段MN的最大值为________.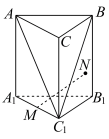 四、解答题17.如图所示,在三棱柱
四、解答题17.如图所示,在三棱柱![]() 中,
中,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,求证:
的中点,求证: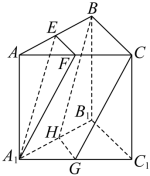 (1)
(1)![]() 平面
平面![]() ; (2)平面
; (2)平面![]() 平面
平面![]() . 18.如图,四棱锥P﹣ABCD的底面为平行四边形.设平面PAD与平面PBC的交线为l,M、N、Q分别为PC、CD、AB的中点.
. 18.如图,四棱锥P﹣ABCD的底面为平行四边形.设平面PAD与平面PBC的交线为l,M、N、Q分别为PC、CD、AB的中点.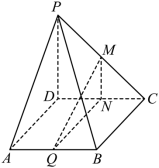 (1)求证:平面MNQ∥平面PAD; (2)求证:BC∥l.
(1)求证:平面MNQ∥平面PAD; (2)求证:BC∥l.
1.D2.B3.C4.B5.B6.B7.C8.B9.BC10.ABD11.BD12.BD13.①②③④14.215.②④16.![]() 17.【详解】(1)证明:∵
17.【详解】(1)证明:∵![]() 分别是
分别是![]() 的中点,∴
的中点,∴![]() ,又在三棱柱
,又在三棱柱![]() 中,
中,![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .(2)证明:由(1)知
.(2)证明:由(1)知![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又∵
,又∵![]() 分别为
分别为![]() 中点, 故
中点, 故![]() ,
,![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,又∵
,又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .18. 【详解】(1)证明:因为M、N、Q分别为PC、CD、AB的中点,底面ABCD为平行四边形,所以MN∥PD,NQ∥AD,又MN⊄平面PAD,PD⊂平面PAD,则MN∥平面PAD,同理可得NQ∥平面PAD,又
.18. 【详解】(1)证明:因为M、N、Q分别为PC、CD、AB的中点,底面ABCD为平行四边形,所以MN∥PD,NQ∥AD,又MN⊄平面PAD,PD⊂平面PAD,则MN∥平面PAD,同理可得NQ∥平面PAD,又![]() 平面MNQ所以平面MNQ∥平面PAD.(2)证明:因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD,又BC⊂平面PBC,平面PBC∩平面PAD=l,所以BC∥l.
平面MNQ所以平面MNQ∥平面PAD.(2)证明:因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD,又BC⊂平面PBC,平面PBC∩平面PAD=l,所以BC∥l.
相关试卷
这是一份高中人教A版 (2019)8.5 空间直线、平面的平行一课一练,共11页。试卷主要包含了下列说法正确的是等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行同步训练题,共4页。试卷主要包含了5 空间直线、平面的平行,下列命题等内容,欢迎下载使用。
这是一份【同步练习】高中数学人教A版(2019)必修第二册--8.5.2 直线与平面平行 同步练习(含解析),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。











