【阶段测试】人教版数学九年级上册-- 期中检测卷（含答案）

人教版数学九年级上册期中检测卷

（时间：120分钟  分数：120分）

一、选择题(共12道题,每小题4分,共48分)

1.下列图形中,既是轴对称图形又是中心对称图形的是(　  　)

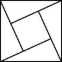
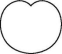
               A         B        C       D

2.若一元二次方程x2+6x+4=0可化成(x+m)2=n的形式,则m+n的值为(　  　)

A.3 B.5 C.6 D.8

3.点A(-3,2)关于原点的对称点是点B,点B关于x轴的对称点是点C,则点C的坐标是(　  　)

A.(3,2) B.(-3,2) C.(3,-2) D.(-2,3)

4.如图,在平面内将该五角星绕其中心旋转180°后所得到的图案是(　  　)

                      A      B       C       D

5.把一个足球垂直于水平地面向上踢,该足球距离地面的高度h(米)与所经过的时间t(秒)之间的关系式为h=10t-t2(0≤t≤14).若存在两个不同的t的值,使足球离地面的高度均为a米,则a的取值范围是(　  　)

A.0≤a≤42 B.0≤a<50  C.42≤a<50 D.42≤a≤50

6.(原创题)已知点A(a,c)在第四象限,则关于x的一元二次方程ax2+bx+c=0的根的情况是(　  　)

A.有两个不相等的实数根 B.有两个相等的实数根

C.无实数根     D.无法判断

7.学校连续三年组织学生参加义务植树,第一年共植树400棵,第三年共植树625棵.设该校植树棵数的年平均增长率为x,根据题意,下列方程正确的是(　  　)

A.625(1-x)2=400  B.400(1+x)2=625

C.625x2=400   D.400x2=625

8.已知抛物线y=x2+mx的对称轴为直线x=2,则关于x的方程x2+mx=5的根是(　  　)

A.0,4  B.1,5   C.1,-5 D.-1,5

9.抛物线的函数解析式为y=(x-2)2-9,则下列结论中,正确的序号为(　  　)

①当x=2时,y取得最小值-9;②若点(3,y1),(4,y2)在其图象上,则y2>y1;③将抛物线向左平移3个单位长度,再向上平移4个单位长度所得抛物线的函数解析式为y=(x-5)2-5;④函数图象与x轴有两个交点,且两交点的距离为6.

A.②③④ B.①②④   C.①③ D.①②③④

10.已知一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,则下面选项正确的是(　  　)

A.1一定不是方程x2+bx+a=0的根

B.0一定不是方程x2+bx+a=0的根

C.1和-1都是方程x2+bx+a=0的根

D.1和-1不都是方程x2+bx+a=0的根

11.如图,已知正方形ABCD与正方形AEFG的边长分别为4 cm,1 cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C,F之间的最小距离为(　  　)

第11题图

A.3 cm   B.2 cm    C.(4-1) cm D.3 cm

12.如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=-1,且过点(0,1).有以下4个结论:①abc>0;②a-b+c>1;③3a+c<0;④若顶点坐标为(-1,2),当m≤x≤1时,y有最大值为2、最小值为-2,则此时m的取值范围是-3≤m≤-1.其中正确结论的个数是(　  　)

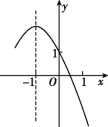
第12题图

A.4 B.3 C.2 D.1

二、填空题(共6道题,每小题4分,共24分)

13.有下列函数:①y=5x-4;②y=x2-6x;③y=2x3-8x2+3;④y=x2-1;⑤y=--2.其中属于二次函数的是　        .(填序号) 

14.已知α,β是关于x的方程x2-x+k-1=0的两个实数根,且α2-2α-β=4,则k的值为　       　. 

15.若点M(-1,y1),N(1,y2),P(,y3)都在抛物线y=-ax2+4ax+a2+1(a>0)上,则y1,y2,y3之间的大小关系是            .(用“<”连接) 

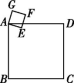
16.将边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置(如图),使得点D落在对角线CF上,EF与AD相交于点H,则HD=　         　.(结果保留根号) 

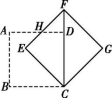
第16题图

17.已知x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等的实数根,且满足(x1-1)(x2-1)=8k2,则k的值为　       　. 

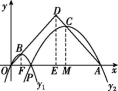
18.如图,已知点A(16,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P,O两点的二次函数y1和过P,A两点的二次函数y2的图象开口均向下,它们的顶点分别为B,C,射线OB与AC相交于点D,当OD=AD=10时,这两个二次函数的最大值之和等于　        　. 

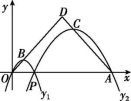
第18题图

三、解答题(共7道题,共78分)

19.(8分)解下列方程:

(1)(x-1)(x+2)=4(x-1);

(2)3x2-6x=1(用公式法).

20.(8分)已知:关于x的方程2x2+kx-1=0.

(1)求证:方程有两个不相等的实数根;

(2)若方程的一个根是x=-1,求另一个根及k的值.

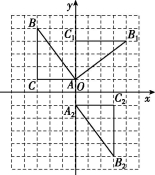
21.(10分)在如图所示的网格图中,每个小正方形的边长均为1个单位长度,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.

(1)试在图中作出△ABC以点A为旋转中心,按顺时针方向旋转90°得到的图形△AB1C1;

(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并写出A,C两点的坐标;

(3)根据(2)中直角坐标系作出与△ABC关于原点对称的图形△A2B2C2,并写出B2,C2两点的坐标.

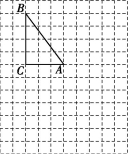
题图

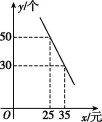
22.(12分)某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图的一次函数关系.

(1)求y与x的函数关系式(不要求写出自变量x的取值范围).

(2)若该玩具某天的销售利润是600元,则当天该玩具的销售单价是多少元?

(3)设该玩具日销售利润为w元,当该玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?

23.(13分)如图①,D为等边三角形ABC内一点,将线段AD绕点A逆时针旋转60°得到AE,连接CE,BD的延长线与AC交于点G,与CE交于点F.

(1)求证:BD=CE.

(2)如图②,连接FA,小颖对该图形进行探究,得出结论:∠BFC=∠AFB=∠AFE.小颖的结论是否正确?若正确,请给出证明;若不正确,请说明理由.

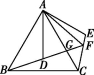
①         ②

24.(13分)如图,A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,运动的时间为t s,一直到达点B为止,点Q以2 cm/s的速度向点D移动,当点P到达点B时点Q随之停止运动.

(1)AP=　　　　cm,BP=　　　　cm,CQ=　　　　cm,DQ=　　　　cm. (用含t的代数式表示) 

(2)当t为多少时,四边形PBCQ的面积为33 cm2?

(3)当t为多少时,点P和点Q的距离为10 cm?

25.(14分)如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A,B(4,0)两点,与y轴交于点C(0,4).

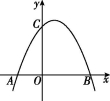
(1)求此抛物线的函数解析式及点A的坐标;

(2)已知点D(1,-1),在直线AD上方的抛物线上有一动点P(x,y)(1<x<4),求△ADP面积的最大值.

期中检测卷

一、选择题

1.C　2.D　3.A　4.C　5.C　6.A　7.B　8.D　9.B　10.D

11.D　解析:如图,连接AF,CF,AC.

∵正方形ABCD与正方形AEFG的边长分别为4 cm,1 cm,

∴∠B=∠G=90°,AB=BC=4 cm,

AG=GF=1 cm,

∴AF===(cm),

AC===4(cm).

∵CF≥AC-AF,∴CF≥3 cm,

∴点C,F之间的最小距离为3 cm.

故选D.

12.A　解析:∵二次函数y=ax2+bx+c的图象的对称轴为直线x=-1,且过点(0,1),∴-=-1,c=1,

∴ab>0,∴abc>0,故①正确.

从图象可以看出,当x=-1时,函数值大于1,因此将x=-1代入解析式,得(-1)2·a+(-1)·b+c>1,

即a-b+c>1,故②正确.

∵-=-1,∴b=2a;从图象可以看出,当x=1时,函数值小于0,∴a+b+c<0,∴3a+c<0,故③正确;

∵二次函数y=ax2+bx+c的顶点坐标为(-1,2),

∴设二次函数的解析式为y=a(x+1)2+2,将(0,1)代入解析式,得1=a+2,解得a=-1,

∴二次函数的解析式为y=-(x+1)2+2,

∴当x=1时,y=-2,

∴根据二次函数的对称性,得-3≤m≤-1,故④正确.

综上所述,①②③④均正确,故有4个正确结论.

故选A.

二、填空题

13.②④　14.-4

15.y1<y3<y2　16.-1

17.1　解析:∵x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等的实数根,∴x1≠x2,

∴x1+x2=-(3k+1),x1x2=2k2+1.

∵(x1-1)(x2-1)=8k2,

即x1x2-(x1+x2)+1=8k2,

∴2k2+1+3k+1+1=8k2,

整理,得2k2-k-1=0,

解得k1=-,k2=1.

∵关于x的方程x2+(3k+1)x+2k2+1=0有两个不相等的实数根,

∴Δ=(3k+1)2-4×1×(2k2+1)>0,

解得k<-3-2或k>-3+2,

∴k=1.

18.6　解析:如图,过点B作BF⊥OA于点F,过点D作DE⊥OA于点E,过点C作CM⊥OA于点M.

∵BF⊥OA,DE⊥OA,CM⊥OA,∴BF∥DE∥CM.

∵OD=AD=10,DE⊥OA,

∴OE=EA=OA=8,

∴由勾股定理得DE==6.

设P(2x,0),根据二次函数的对称性得OF=PF=x.

∵BF∥DE∥CM,

∴△OBF∽△ODE,△ACM∽△ADE,

∴=,=.

∵AM=PM=(OA-OP)=(16-2x)=8-x,

即=,=,

∴BF=x,CM=6-x,

∴BF+CM=6.

三、解答题

19.解:(1)(x-1)(x+2)-4(x-1)=0,

(x-1)(x+2-4)=0,

∴x1=1,x2=2.

(2)原方程可化3x2-6x-1=0,

∴Δ=(-6)2-4×3×(-1)=48,

∴x==,

∴x1=,x2=.

20.(1)证明:由题意,得Δ=k2-4×2×(-1)=k2+8.

∵无论k取何值,k2≥0,

∴k2+8>0,即Δ>0,

∴方程2x2+kx-1=0有两个不相等的实数根.

(2)解:把x=-1代入原方程,得2-k-1=0,

∴k=1,

∴原方程化为2x2+x-1=0,

解得x1=-1,x2=,

∴方程的另一个根为x=,k的值为1.

21.

答图

解:(1)如图,△AB1C1即为所求.

(2)直角坐标系如图,点A的坐标为(0,1),点C的坐标为(-3,1).

(3)如图,△A2B2C2即为所求,点B2的坐标为(3,-5),点C2的坐标为(3,-1).

22.解:(1)设一次函数的关系式为y=kx+b(k≠0),

把(25,50)和(35,30)代入,得解得

∴y与x的函数关系式为y=-2x+100.

(2)设当天该玩具的销售单价是x元,

由题意,得(x-10)×(-2x+100)=600,解得x1=40,x2=20,

∴当天该玩具的销售单价是40元或20元.

(3)根据题意,得

w=(x-10)×(-2x+100)=-2(x-30)2+800.

∵-2<0,∴当x=30时,w有最大值,最大值为800.

故当该玩具的销售单价定为30元时,日销售利润最大,最大利润是800元.

23.(1)证明:∵线段AD绕点A逆时针旋转60°得到AE,

∴AD=AE,∠DAE=60°.

∵∠BAC=60°,∴∠BAC=∠DAE,∴∠BAD=∠CAE.

在△ABD和△ACE中,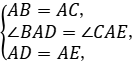

∴△ABD≌△ACE(SAS),∴BD=CE.

(2)解:结论正确.证明如下:

如图,过点A作BD,CF的垂线,垂足分别为M,N.

由(1)知△ABD≌△ACE,∴∠ABD=∠ACE.

又∵∠AGB=∠CGF,∴∠BFC=∠BAC=60°,∴∠BFE=120°.

由(1)知△ABD≌△ACE,∴BD=CE,S△ABD=S△ACE,

∴AM·BD=CE·AN,∴AM=AN.

在Rt△AFM和Rt△AFN中,

∴Rt△AFM≌Rt△AFN(HL),∴∠AFM=∠AFN,

∴∠BFC=∠AFB=∠AFE=60°.

24.解:(1)3t　(16-3t)　2t　(16-2t)

(2)依题意,得[(16-3t)+2t]×6=33,

整理,得16-t=11,

解得t=5,

∴当t为5时,四边形PBCQ的面积为33 cm2.

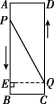
(3)如图,过点Q作QE⊥AB于点E,

则PE=|(16-3t)-2t|=|16-5t|.

依题意,得|16-5t|2+62=102,

即(16-5t)2=82,

解得t1=,t2=,

∴当t为或时,点P和点Q的距离为10 cm.

25.解:(1)把B(4,0)和C(0,4)代入y=-x2+bx+c,得

解得

∴抛物线的函数解析式为y=-x2+x+4.

令y=0,得-x2+x+4=0,解得x=4(舍去)或x=-2,

∴A(-2,0).

(2)过点P作PE⊥x轴于点F,与AD交于点E,如图.

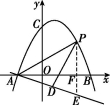
设直线AD的解析式为y=kx+m(k≠0),则

解得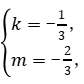

∴直线AD的解析式为y=-x-.

∵P(x,y),即P(x,-x2+x+4),∴E(x,-x-),

∴PE=-x2+x+,

∴S△ADP=S△APE-S△DPE

=PE·(x+2)-PE·(x-1)

=PE·(2+1)=×(-x2+x+)×3

=-x2+2x+7=-(x-)2+.

∵1<<4,∴△ADP面积的最大值为.