初中数学人教版八年级上册13.1.1 轴对称优秀复习练习题

第十三章  轴对称 达标测试卷

一、选择题(每小题3分,共30分)

1.下列图形中,是轴对称图形的是(　 　)

A    B     C      D

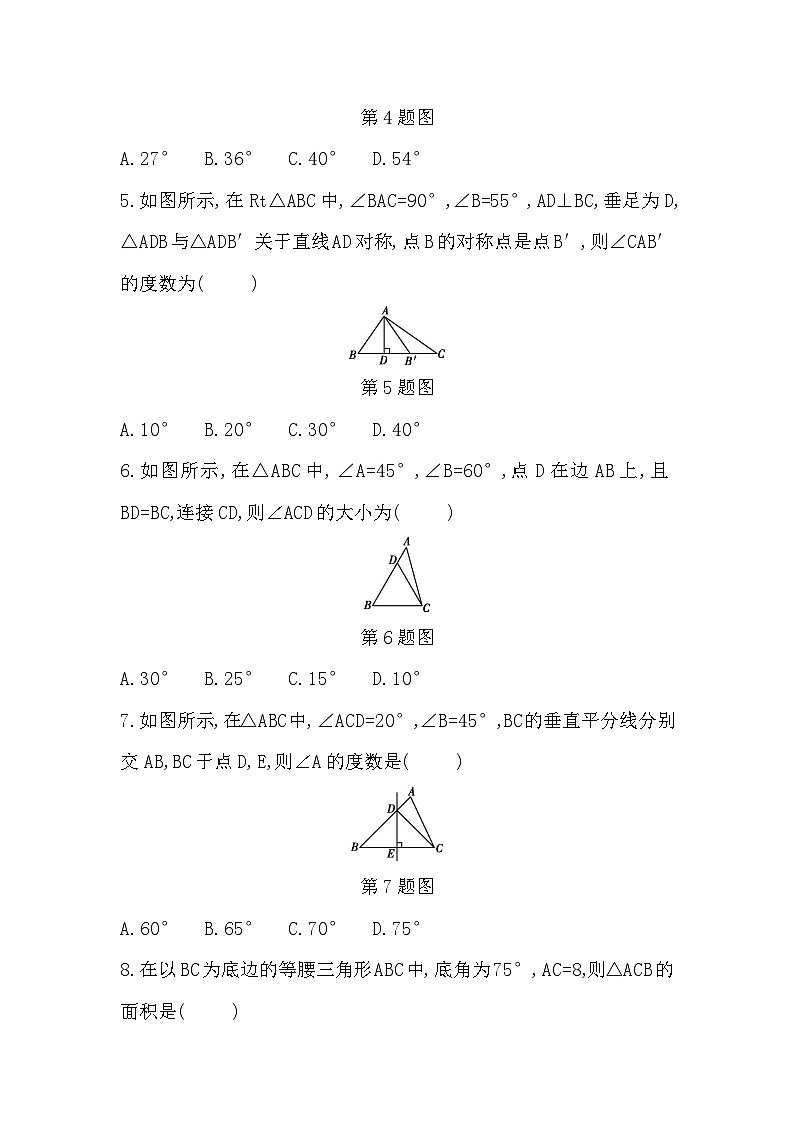
2.如图所示,在△ABC中,∠A=87°,∠ABC的平分线BD交AC于点D,E是BC的中点,且DE⊥BC,那么∠C的度数为(　 　)

第2题图

A.16° B.28° C.31° D.62°

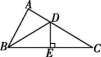
3.如图所示,∠AOB=30°,点C在射线OB上,若OC=6,则点C到OA的距离等于(　 　)

第3题图

A.3　  B.2    C.3  D.12

4.如图所示,BE⊥AC于点D,且AB=BC,BD=ED,若∠ABC=54°,则∠E等于(　 　)

第4题图

A.27° B.36° C.40° D.54°

5.如图所示,在Rt△ABC中,∠BAC=90°,∠B=55°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为(　 　)

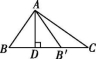
第5题图

A.10° B.20° C.30° D.40°

6.如图所示,在△ABC中,∠A=45°,∠B=60°,点D在边AB上,且BD=BC,连接CD,则∠ACD的大小为(　 　)

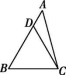
第6题图

A.30° B.25° C.15° D.10°

7.如图所示,在△ABC中,∠ACD=20°,∠B=45°,BC的垂直平分线分别交AB,BC于点D,E,则∠A的度数是(　 　)

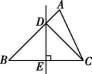
第7题图

A.60° B.65° C.70° D.75°

8.在以BC为底边的等腰三角形ABC中,底角为75°,AC=8,则△ACB的面积是(　 　)

A.12 B.24 C.18 D.16

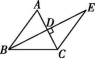
9.如图所示,在△ABC中,AB=AC,AD,BE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于CP+EP最小值的是(　 　)

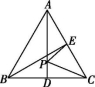
第9题图

A.AC B.AD C.BE D.BC

10.如图所示,△ABC是等边三角形,线段AD是△ABC中BC边上的高,DE⊥AC于点E,则的值为(　 　)

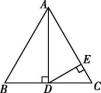
第10题图

A.8 B.6 C.9 D.4

二、填空题(每小题3分,共18分)

11.墙上有一个数字式电子钟,在对面墙上的镜子里看到该电子钟显示的时间如图所示,那么它的实际时间是　           　. 

第11题图

12.若一个等腰三角形的三个内角的度数之比为1∶1∶3,则这个等腰三角形的顶角的度数为　　           　　. 

13.如图所示,在△ABC中,∠C=90°,∠A=15°,斜边AB的垂直平分线交AC于点E,交AB于点D,AE=10 cm,则BC=　　           　　cm. 

第13题图

14.如图所示,在△ABC中,∠ABC=90°,AD=DC,AE⊥BD,若∠DAE=28°,则∠BAE=　　           　　. 

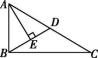
第14题图

15.如图所示,线段AB,BC的垂直平分线l1,l2相交于点O,若∠1=38°,则∠AOC的度数为　　           　　. 

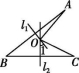
第15题图

16.在△ABC中,AB=AC,AB的垂直平分线交直线AC于点D,若∠BDA =64°,则∠ACB的度数为　　           　　. 

三、解答题(共52分)

17.(8分)如图所示,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-3,-2).

(1)图中点C关于x轴对称的点D的坐标是　　　　; 

(2)如果将点B沿着与y轴平行的方向向上平移5个单位长度得到点B1,那么A,B1两点之间的距离是　　　　; 

(3)在(1)的条件下,求三角形ACD的面积.

18.(8分)如图所示,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=8,求CE的长.

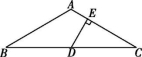
19.(8分)如图所示,在△ABC中,AB=AC,AD是△ABC底边BC上的中线,点P为线段AB上一点.

(1)在AD上找一点E,使得PE+EB的值最小.

(2)若点P为AB的中点,当∠BPE满足什么条件时,△ABC是等边三角形?说明理由.

20.(8分)如图所示,已知在等边三角形ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.

21.(10分)如图所示,在△ABC中,AB=AC,AD是高,AM是△ABC外角

∠CAE的平分线.

(1)作∠ADC的平分线DN;(尺规作图,保留作图痕迹,不写作法和

证明)

(2)设DN与AM交于点F,判断△ADF的形状,并说明理由.

22.(10分)如图所示,过等边三角形ABC的边AB上一点P作PE⊥AC于点E,Q为BC延长线上一点,且PA=CQ,连接PQ交边AC于点D.

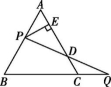
(1)求证:PD=QD;

(2)若△ABC的边长为1,求DE的长.

第十三章　达标测试卷答案

[测控导航表]

一、选择题

1.B　2.C　3.A　4.A　5.B　6.C　7.C　8.D　

9.C　解析:如图所示,连接PB.

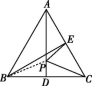
∵AB=AC,BD=CD,∴AD⊥BC,

∴PB=PC,∴PC+PE=PB+PE.

∵PE+PB≥BE,

∴点P,B,E在同一条直线上时,PB+PE的值最小,最小值为BE的长度.故选C.

10.A　解析:∵△ABC是等边三角形,

∴AB=AC=BC,∠BAC=∠C=60°.

∵AB=AC,AD⊥BC,

∴BD=CD=BC,∠DAC=∠BAC=30°,

∴AC=2CD,S△ADC=S△ABC.

∵DE⊥AC,∴∠DEC=90°,∴∠EDC=90°-∠C=30°,

∴CD=2EC,∴AC=4EC,

∴S△ADC=4S△CDE,S△ABC=8S△CDE,

∴=8.

故选A.

二、填空题

11.12:51　12.108°　13.5　14.31°

15.76°　解析:连接BO并延长BO到点P,如图所示.

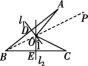
∵线段AB,BC的垂直平分线l1,l2相交于点O,

∴AO=OB=OC,∠BDO=∠BEO=90°,

∴∠DOE+∠ABC=180°.

∵∠DOE+∠1=180°,∴∠ABC=∠1=38°.

∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C.

∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,

∴∠AOC=∠AOP+∠COP=∠A+∠ABO+∠OBC+∠C=2∠ABC=2×38°=76°.

16.61°或29°　解析:如图①所示,∵DE垂直平分AB,

∴AD=BD,∴∠BAC=∠ABD.

∵∠BDA=64°,∴∠BAC=∠ABD=58°.

∵AB=AC,∴∠ACB=61°.

如图②所示,∵DE垂直平分AB,∴AD=BD,

∴∠BAD=∠ABD.

∵∠BDA=64°,∴∠BAD=∠ABD=58°,

∴∠BAC=122°.

∵AB=AC,∴∠ACB=29°.

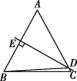
①       ②

三、解答题

17.解:(1)(3,2)

(2)3

(3)三角形ACD的面积为×4×3=6.

18.解:如图所示,连接AD.

∵AB=AC,D为BC的中点,

∴AD⊥BC且AD平分∠BAC.

∵∠BAC=120°,

∴∠DAE=60°.

∵DE⊥AC,

∴∠ADE=90°-60°=30°.

在Rt△ADE中,

∵AE=8,∠ADE=30°,

∴AD=2AE=16.

∵AB=AC,∠BAC=120°,

∴∠C=∠B=30°,

∴AC=2AD=32,

∴CE=AC-AE=32-8=24.

19.解:(1)如图所示,连接CP交AD于点E,则点E为所求.

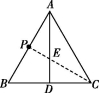
(2)∠BPE=90°.理由如下:

∵∠BPE=90°,∴CP⊥AB.

∵点P为AB的中点,

∴CP垂直平分AB,∴CA=CB.

∵AB=AC,∴AB=AC=BC,

∴△ABC是等边三角形.

20.求证:(1)DE=2DM;

(2)M是BE的中点.

证明:(1)∵三角形ABC是等边三角形,

∴∠ACB=∠ABC=60°.

又∵CE=CD,

∴∠E=∠CDE.

又∵∠ACB=∠E+∠CDE,

∴∠E=∠ACB=30°.

∵DM⊥BC,

∴DE=2DM.

(2)连接BD,如图所示.

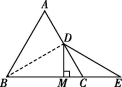
∵在等边三角形ABC中,D是AC的中点,

∴∠DBC=∠ABC=×60°=30°.

由(1)知∠E=30°,

∴∠DBC=∠E,

∴DB=DE.

又∵DM⊥BC,

∴M是BE的中点.

21.解:(1)如图所示.

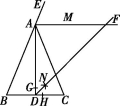
(2)△ADF的形状是等腰直角三角形.

理由如下:∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.

∵AF平分∠EAC,∴∠EAF=∠FAC,

∴∠FAD=∠FAC+∠DAC=∠EAC+∠BAC=×180°=90°,

∴△ADF是直角三角形.

∵AB=AC,∴∠B=∠ACB.

∵∠EAC=2∠EAF=∠B+∠ACB,∴∠EAF=∠B,

∴AF∥BC,∴∠AFD=∠FDC.

∵DF平分∠ADC,∴∠ADF=∠FDC=∠AFD,

∴AD=AF,∴△ADF是等腰直角三角形.

22.(1)证明:如图所示,过点P作PF∥BC交AC于点F,

∴∠AFP=∠ACB,∠FPD=∠Q,∠PFD=∠QCD.

∵△ABC为等边三角形,

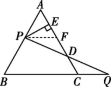
∴∠A=∠ACB=60°,

∴∠A=∠AFP=60°,

∴△APF是等边三角形,

∴AP=PF.

又∵AP=CQ,

∴PF=CQ,

∴△PFD≌△QCD,

∴PD=QD.

(2)解:∵△APF是等边三角形,PE⊥AC,

∴AE=EF.

∵△PFD≌△QCD,

∴CD=DF,

∴DE=EF+DF=AE+CD=AC.

∵AC=1,

∴DE=.