初中数学12.1 全等三角形精品课堂检测

第十二章  全等三角形 达标测试卷

一、选择题(每小题3分,共30分)

1.下列各条件中,不能作出唯一三角形的是(　 　)

A.已知两边和夹角      B.已知两角和夹边

C.已知两边和其中一边的对角   D.已知三边

2.下列条件能判定△ABC≌△DEF的一组是(　 　)

A.AB=DE,BC=EF,∠A=∠D 

B.∠A=∠D,∠B=∠E,∠C=∠F

C.AB=DE,△ABC的周长等于△DEF的周长 

D.∠A=∠D,∠C=∠F,AC=DF

3.如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AE+DE=3 cm,那么AC等于(　 　)

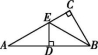
第3题图

A.2 cm B.3 cm C.4 cm D.5 cm

4.如图所示,为测量池塘两端A,B的距离,学校课外实践小组在池塘旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得

∠ACD=∠ACB,CD=CB,再测得AD的长就是AB的长.其依据是(　 　)

第4题图

A.SSS B.SAS C.ASA D.AAS

5.如图所示,在CD上求一点P,使它到OA,OB的距离相等,则点P是(　 　)

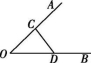
第5题图

A.线段CD的中点     B.OA与OB的垂直平分线的交点

C.OA与CD的垂直平分线的交点 D.CD与∠AOB的平分线的交点

6.如图所示为正方形网格,则∠1+∠2+∠3等于(　 　)

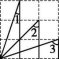
第6题图

A.105° B.120° C.115° D.135°

7.如图所示,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是(　 　)

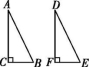
第7题图

A.∠A=∠D,∠B=∠E  B.AC=DF,AB=DE

C.∠A=∠D,AB=DE  D.AC=DF,CB=FE

8.如图所示,在AB,AC上各取一点E,D,使AE=AD,连接BD,CE相交于点O,再连接AO,BC,若∠1=∠2,则图中的全等三角形共有(　 　)

第8题图

A.5对  B.6对   C.7对  D.8对

9.如图所示,在△ABC中,AB=AC,点D是△ABC外一点,连接AD,BD,CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC,若

∠ABC=62°,则∠BDC的度数为(　 　)

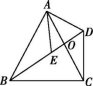
第9题图

A.56° B.60° C.62° D.64°

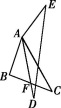
10.如图所示,在△ABD和△ACE中,AB=AD,AC=AE,AB>AC,∠DAB=∠CAE =50°,连接BE,CD相交于点F,连接AF.下列结论:①BE=CD;②∠EFC= 50°;③AF平分∠DAE;④FA平分∠DFE.其中正确的有(　 　)

第10题图

A.1个 B.2个 C.3个 D.4个

二、填空题(每小题3分,共18分)

11.肖老师为班级中每位同学准备了长分别为a,b,c的三根木条,所有同学都用三根木条首尾顺次拼接组成三角形,这时小陈同学说:“我们所有人的三角形的形状和大小是完全一样的.”小陈同学的说法依据是　          　. 

12.如图所示,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为　　          　. 

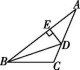
第12题图

13.如图所示,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为

2米/秒,则这个人运动到点M所用的时间是　　          　秒. 

第13题图

14.我们把顶点在小正方形顶点上的三角形叫做格点三角形,在如图所示的方格纸中,除了格点三角形ABC外,可画出与△ABC全等的格点三角形　　          个. 

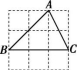
第14题图

15.如图所示,△ABC≌△A1B1C,若∠A=50°,∠A1B1C=45°,∠ACB1= 65°,则∠α的度数为　　          　. 

第15题图

16.如图所示,在平面直角坐标系中,已知点A(2,0),B(0,4),若△BOC与△ABO全等,则点C的坐标为　　          　. 

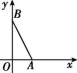
第16题图

三、解答题(共52分)

17.(8分)如图所示,已知△ABC和△ADC有公共边AC,且AB=AD,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使∠B =∠D,并说明理由.

18.(8分)小明利用一根3 m长的

竿子来测量路灯的高度.他的方法是这样的:如图所示,在路灯前选一点P,使BP=3 m,并测得∠APB=70°,然后把竖直的竿子CD(CD=3 m)在BP的延长线上移动,使∠DPC=20°,此时量得BD=11.2 m.根据这些数据,小明计算出了路灯的高度.你能计算出路灯的高度吗?

19.(8分)如图所示,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且BE=CF,DB=DC,求证:AD是∠EAC的平分线.

20.(8分)如图所示,在△ABC中,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t s后,它们分别爬行到了D,E处,设DC与BE的交点为F.

(1)求证:△ACD≌△CBE.

(2)在小蚂蚁的爬行过程中,∠BFC的大小有无变化?请说明理由.

21.(10分)如图所示,点B在线段AC上,点E在线段BD上,∠ABD=

∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点.试探索BM和BN的关系,并证明你的结论.

22.(10分)已知:AD=AC,AB=AE,AD交BC于点F.

(1)如图①所示,当∠BAD=∠CAE时,设DE交BC于点N,交AC于点M,求证:∠AMD=∠AFC.

(2)如图②所示,当∠BAC+∠DAE=180°,且点F为BC的中点时,线段DE与线段AF之间存在某种数量关系,写出你的结论,并加以证明.

①             ②

第十二章　达标测试卷答案

[测控导航表]

一、选择题

1.C　2.D　3.B　4.B　5.D　6.D　7.A　8.A　

9.A　解析:∵∠EAD=∠BAC,

∴∠BAC-∠EAC=∠EAD-∠EAC,

即∠BAE=∠CAD.

在△ABE和△ACD中,

∴△ABE≌△ACD(SAS),∴∠ABD=∠ACD.

∵∠BOC是△ABO和△DCO的外角,

∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC,

∴∠ABD+∠BAC=∠ACD+∠BDC,

∴∠BAC=∠BDC.

∵AB=AC,∴∠ABC=∠ACB=62°,

∴∠BAC=180°-∠ABC-∠ACB=180°-62°-62°=56°,

∴∠BDC=∠BAC=56°.

故选A.

10.C　解析:∵∠DAB=∠CAE=50°,

∴∠BAE=∠DAC=50°+∠BAC.

在△BAE和△DAC中,

∴△BAE≌△DAC(SAS),

∴BE=CD,∠AEB=∠ACD,故①正确.

如图所示,设BE交AC于点G,

则∠EFC=∠CGE-∠ACD=∠CGE-∠AEB=∠CAE=50°,

故②正确.

如图所示,过点A作AI⊥BE于点I,AJ⊥CD于点J.

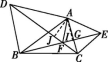
∵S△BAE=S△DAC,∴AI·BE=AJ·CD,∴AI=AJ,

∴点A在∠DFE的平分线上,

∴FA平分∠DFE,故④正确.

假设∠DAF=∠EAF,则∠DAF-∠DAB=∠EAF-∠CAE,

∴∠BAF=∠CAF.

∵∠AFD=∠AFE,∠BFD=∠CFE,

∴∠AFD+∠BFD=∠AFE+∠CFE,

∴∠AFB=∠AFC.

在△AFB和△AFC中,

∴△AFB≌△AFC(ASA),∴AB=AC,这与已知条件相矛盾,

∴∠DAF≠∠EAF,故③错误.

故选C.

二、填空题

11.SSS

12.2

13.4　

14.15

15.20°　解析:∵△ABC≌△A1B1C,∠A1B1C=45°,

∴∠ABC=∠A1B1C=45°.

∵∠A=50°,

∴∠ACB=180°-∠ABC-∠A=85°.

∵∠ACB1=∠65°,

∴∠α=∠ACB-∠ACB1=85°-65°=20°.

16.(2,4),(-2,0)或(-2,4)　解析:如图所示,则C(-2,0),C′(-2,4),C′′(2,4).

故答案为(2,4),(-2,0)或(-2,4).

三、解答题

17.解:添加条件:CB=CD(答案不唯一).

理由:在△ABC和△ADC中,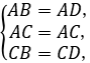

∴△ABC≌△ADC(SSS),

∴∠B=∠D.

18.解:∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,

∴∠DCP=∠APB=70°.

在△CPD和△PAB中,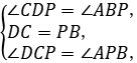

∴△CPD≌△PAB(ASA),∴DP=AB.

∵DB=11.2 m,PB=3 m,

∴AB=DP=11.2-3=8.2(m).

答:路灯的高度是8.2 m.

19.证明:∵DE⊥AB交AB的延长线于点E,DF⊥AC于点F,

∴∠BED=∠CFD,

∴△BDE与△CDF是直角三角形.

在Rt△BDE和Rt△CDF中,

∴Rt△BDE≌Rt△CDF(HL),

∴DE=DF.

又∵DE⊥AB交AB的延长线于点E,DF⊥AC于点F,

∴AD是∠EAC的平分线.

20.(1)证明:∵小蚂蚁同时从A,C出发,速度相同,

∴t s后两只小蚂蚁爬行的路程AD=CE.

∵在△ACD和△CBE中,∴△ACD≌△CBE(SAS).

(2)解:无变化.理由如下:∵△ACD≌△CBE,∴∠EBC=∠ACD,

∴∠BFC=180°-∠EBC-∠BCD=180°-∠ACD-∠BCD=180°-∠ACB.

∵∠A=∠ABC=∠ACB,∴∠ACB=60°,

∴∠BFC=180°-60°=120°,∴∠BFC的大小无变化.

21.解:BM=BN,BM⊥BN.证明如下:

在△ABE和△DBC中,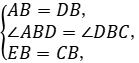

∴△ABE≌△DBC(SAS),

∴∠BAE=∠BDC,AE=CD.

∵M,N分别是AE,CD的中点,∴AM=DN.

在△ABM和△DBN中,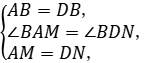

∴△ABM≌△DBN(SAS),

∴BM=BN,∠ABM=∠DBN.

∵∠ABD=∠DBC,∠ABD+∠DBC=180°,

∴∠ABD=∠ABM+∠MBE=90°,

∴∠MBE+∠DBN=90°,即BM⊥BN.

故BM=BN,BM⊥BN.

22.(1)证明:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,

∴∠BAC=∠EAD.

在△BAC和△EAD中,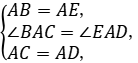

∴△BAC≌△EAD(SAS),∴∠C=∠D.

又∠DNF=∠CNM,∴∠DNF+∠D=∠CNM+∠C,∴∠AFC=∠AMD.

(2)解:DE=2AF.

证明:延长AD至G,使AF=GF,连接CG,如图所示.

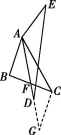
∵F为BC的中点,∴BF=CF.

在△AFB和△GFC中,∴△AFB≌△GFC(SAS),

∴AB=GC,∠BAF=∠CGF,

∴AB∥CG,

∴∠BAC+∠ACG=180°.

∵∠BAC+∠DAE=180°,∴∠ACG=∠DAE.

∵AB=AE,∴AE=CG.

在△DAE和△ACG中,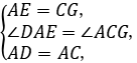

∴△DAE≌△ACG(SAS),∴DE=AG=2AF,∴DE=2AF.