初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.4 整式的乘法精品同步练习题

第十四章  整式的乘法与因式分解 达标测试卷

一、选择题(每小题3分,共30分)

1.下列计算中,正确的是(　 　)

A.a6÷a2=a3  B.(2x2)3=8x6

C.3a2×2a2=6a2 D.(-1)0×a=-a

2.计算2x2y·(x-3xy2)的结果为(　 　)

A. 2x3y-3x3y3  B.2xy2-6x3y3 

C.2x3y-6x3y3  D.2x2y+6x3y3

3.下列从左至右的变形中,属于因式分解的是(　 　)

A.4a2-8a=a(4a-8)

B.-x2+y2=(-x+y)(-x-y)

C.x2-x+=

D.x2+1=x

4.已知△ABC的三边长a,b,c满足(a-b)(c2-a2-b2)=0,则△ABC的形状是(　 　)

A.等腰三角形或直角三角形 B.等腰直角三角形

C.等腰三角形     D.直角三角形

5.计算(12x3-8x2+16x)÷(-4x)的结果是(　 　)

A.-3x2+2x-4  B.-3x2-2x+4  C.-3x2+2x+4  D.3x2-2x+4

6.已知x,y满足则x2-y2的值为(　 　)

A.8 B.-8 C.10 D.-10

7.若(x+2)(x+a)=x2+bx-2,则a+b等于(　 　)

A.-1 B.0 C.1 D.2

8.有三个连续奇数,若中间一个数为n,则这三个连续奇数的积为(　 　)

A.4n3-n  B.n3-4n  C.8n2-8n　 D.4n3-2n

9.已知(x2+y2+1)2-4=0,那么x2+y2+2 023的值为(　 　)

A.2 024    B.2 022    C.2 022或2 024   D.不能确定

10.如图所示,长方形ABCD的周长是12 cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH.若正方形ABEF和ADGH的面积之和为

20 cm2,则长方形ABCD的面积是(　 　)

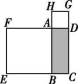
A.6 cm2 B.7 cm2 C.8 cm2 D.4 cm2

二、填空题(每小题3分,共18分)

11.(2022西宁)计算:3x2·(-2xy3)=　             　. 

12.(2022临沂)因式分解:2x2-4x+2= 　           　. 

13.若2a+b=3,则4a+2b=　6　;若3m+2n=4,则8m·4n=　       　. 

14.已知x2-mx+49是完全平方式,则m=　           　. 

15.若多项式A除以2x2-3,得到的商式为3x-4,余式为5x+2,则A=　           　. 

16.若实数x满足x2-2x-1=0,则2x3-2x2-6x+2 020=　           . 

三、解答题(共52分)

17.(6分)计算:

(1)(x2)3·(x2)4÷(x2)5;

(2)a(a-3b)+(a+b)2-a(a-b).

18.(6分)分解因式:

(1)3b2-12b+12;

(2)a3(x-y)+ab2(y-x).

19.(8分)化简求值:

(1)已知(x-1)(2x-1)-(x+1)2+1,其中x2-5x=3;

(2)已知[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷(-2x),其中x=1,y=-2.

20.(10分)将4个数a,b,c,d排成两行两列,两边各加一条竖直线记成,定义 =ad-bc,若=24,求x的值.

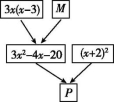
21.(10分)如图所示,已知上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.

(1)求整式M,P;

(2)将整式P因式分解;

(3)求整式P的最小值.

22.(12分)将图①中正方形的阴影部分裁剪下来,重新拼成一个如图②所示的长方形.

(1)比较图②和图①阴影部分的面积,可以推出公式:(x+y)(x-y) =　　　　. (用含x,y的式子表示) 

(2)运用你所得到的公式,计算下列各题:

①(2m+n-p)(2m-n+p);

②(a+2b-3c)2-(a-2b+3c)2.

①

②

第十四章　达标测试卷答案

[测控导航表]

一、选择题

1.B　2.C　3.C　4.A　5.A　6.B　7.B　8.B　

9.A　解析:∵(x2+y2+1)2-4=0,

∴(x2+y2+1)2=4.

∵x2+y2≥0,∴x2+y2+1=2,

∴x2+y2=1,

∴x2+y2+2 023=1+2 023=2 024.

故选A.

10.C　解析:设AB=x cm,AD=y cm,

则2(x+y)=12,且x2+y2=20,

即x+y=6,x2+y2=20,

∴(x+y)2=x2+2xy+y2=20+2xy=62,

∴2xy=16,

∴xy=8,即长方形ABCD的面积是8 cm2.

故选C.

二、填空题

11.-6x3y3　12.2(x-1)2　13.6　16　14.±14

15.6x3-8x2-4x+14　解析:∵多项式A除以2x2-3,得到的商式为3x-4,余式为5x+2,

∴A=(2x2-3)(3x-4)+5x+2

=6x3-8x2-9x+12+5x+2

=6x3-8x2-4x+14.

故答案为6x3-8x2-4x+14.

16.2 022　解析:∵x2-2x-1=0,

∴x2=2x+1,x2-2x=1,

∴原式=2x·x2-2x2-6x+2 020

=2x(2x+1)-2x2-6x+2 020

=4x2+2x-2x2-6x+2 020

=2x2-4x+2 020

=2(x2-2x)+2 020

=2×1+2 020

=2 022.

三、解答题

17.解:(1)(x2)3·(x2)4÷(x2)5

=x6·x8÷x10

=x14÷x10

=x4.

(2)a(a-3b)+(a+b)2-a(a-b)

=a2-3ab+a2+2ab+b2-a2+ab

=a2+b2.

18.解:(1)3b2-12b+12

=3(b2-4b+4)

=3(b-2)2.

(2)a3(x-y)+ab2(y-x)

=a(x-y)(a2-b2)

=a(x-y)(a+b)(a-b).

19.解:(1)(x-1)(2x-1)-(x+1)2+1

=2x2-x-2x+1-x2-2x-1+1

=x2-5x+1.

当x2-5x=3时,原式=3+1=4.

(2)[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷(-2x)

=(x2-4xy+4y2+x2-4y2-4x2+2xy)÷(-2x)

=(-2x2-2xy)÷(-2x)

=x+y.

当x=1,y=-2时,原式=1+(-2)=-1.

20.解:由题意,得(x+1)2-(x-1)2=24,

x2+2x+1-(x2-2x+1)=24,

x2+2x+1-x2+2x-1=24,

4x=24,

x=6.

21.解:(1)根据题意,得M=3x2-4x-20-3x(x-3)

=3x2-4x-20-3x2+9x

=5x-20;

P=3x2-4x-20+(x+2)2

=3x2-4x-20+x2+4x+4

=4x2-16.

(2)P=4x2-16

=4(x2-4)

=4(x+2)(x-2).

(3)∵P=4x2-16,x2≥0,

∴当x=0时,整式P的最小值为-16.

22.解:(1)x2-y2

(2)①原式=[2m+(n-p)]·[2m-(n-p)]

=(2m)2-(n-p)2

=4m2-n2+2np-p2.

②原式=[(a+2b-3c)+(a-2b+3c)]·[(a+2b-3c)-(a-2b+3c)]

=2a(4b-6c)

=8ab-12ac.