【阶段测试】高中数学人教A版(2019)选修第一册--第 3 章圆锥曲线的方程(单元测试)含解析
展开![]() 第 3 章圆锥曲线的方程(单元测试)
第 3 章圆锥曲线的方程(单元测试)
考试时间:120分钟 满分:150分
一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.
1.双曲线![]() =1的焦点坐标是( )
=1的焦点坐标是( )
A.(0,±1) B.(±1,0) C.![]() D.
D.![]()
2.椭圆![]() +
+![]() =1的离心率是( )
=1的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.抛物线y2=﹣2x的准线方程为( )
A.x=﹣1 B.x=1 C.![]() D.
D.![]()
4.已知平面α和两条异面直线a,b满足a⊂α,b⊥α,平面α内的动点M到两条直线a,b的距离相等,则点M的轨迹是( )
A.两条直线 B.椭圆 C.双曲线 D.抛物线
5.设F是双曲线C:![]() 的右焦点,l是双曲线C的一条渐近线,过F作一条直线垂直于l,垂足为P,则sin∠OFP的值为( )
的右焦点,l是双曲线C的一条渐近线,过F作一条直线垂直于l,垂足为P,则sin∠OFP的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.直线2x+3y=0是双曲线![]() 的一条渐近线,则实数a的值为( )
的一条渐近线,则实数a的值为( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
7.已知双曲线C与椭圆![]() =1有共同的焦点,且焦点到该双曲线渐近线的距离等于1,则双曲线C的方程为( )
=1有共同的焦点,且焦点到该双曲线渐近线的距离等于1,则双曲线C的方程为( )
A.![]() =1 B.y2﹣
=1 B.y2﹣![]() =1 C.
=1 C.![]() =1 D.y2﹣
=1 D.y2﹣![]() =1
=1
8.已知F1,F2是椭圆![]() 的左,右焦点,点A是椭圆上的一个动点,则△AF1F2的内切圆的半径的最大值是( )
的左,右焦点,点A是椭圆上的一个动点,则△AF1F2的内切圆的半径的最大值是( )
A.1 B.![]() C.
C.![]() D.
D.![]()
二、多选题:本大题共4小题,每个小题5分,共20分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.
9.下列有关双曲线2x2﹣y2=8的性质说法正确的是( )
A.离心率为![]() B.顶点坐标为(0,±2)
B.顶点坐标为(0,±2)
C.实轴长为4 D.虚轴长为![]()
10.在平面直角坐标系xOy中,抛物线y2=6x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.若直线AF的斜率![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.准线方程为x=﹣3 B.焦点坐标![]()
C.点P的坐标为![]() D.PF的长为3
D.PF的长为3
11.已知椭圆C:![]() 内一点M(1,2),直线l与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是( )
内一点M(1,2),直线l与椭圆C交于A,B两点,且M为线段AB的中点,则下列结论正确的是( )
A.椭圆的焦点坐标为(2,0)、(﹣2,0)
B.椭圆C的长轴长为4![]()
C.直线l的方程为x+y﹣3=0
D.|AB|=![]()
12.定义:以双曲线的实轴为虚轴,虚轴为实轴的双曲线与原双曲线互为共轭双曲线.以下关于共轭双曲线的结论正确的是( )
A.与![]() 共轭的双曲线是
共轭的双曲线是![]()
B.互为共轭的双曲线渐近线不相同
C.互为共轭的双曲线的离心率为e1,e2,则e1e2≥2
D.互为共轭的双曲线的4个焦点在同一圆上
三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知O为坐标原点,双曲线![]()
![]() =1(a>0,b>0)的左焦点为F,左顶点为A,过点F向双曲线的一条渐近线作垂线,垂足为P,且|AF|+|FP|=|OF|,则该双曲线的离心率为 .
=1(a>0,b>0)的左焦点为F,左顶点为A,过点F向双曲线的一条渐近线作垂线,垂足为P,且|AF|+|FP|=|OF|,则该双曲线的离心率为 .
14.若关于x,y的方程![]() =1表示的是曲线C,给出下列四个命题:
=1表示的是曲线C,给出下列四个命题:
①若C为椭圆,则1<t<3;
②若C为双曲线,则t>3或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<2.
其中正确的命题是 .(把所有正确命题的序号都填在横线上)
15.已知双曲线C:![]()
![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,左、右顶点分别为A1,A2,点P是双曲
=1(a>0,b>0)的左、右焦点分别为F1,F2,左、右顶点分别为A1,A2,点P是双曲
线C上不同于A1,A2的任意一点,若△PF1F2与△PA1A2的面积之比为![]() :1,则双曲线C的离心率为 .
:1,则双曲线C的离心率为 .
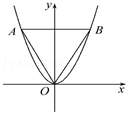
16.如图所示,等边三角形OAB的边长为8![]() ,且其三个顶点均在抛物线 C:x2=2py(p>0)上.则抛物线C的方程为 .
,且其三个顶点均在抛物线 C:x2=2py(p>0)上.则抛物线C的方程为 .
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.求适合下列条件的椭圆标准方程:
(1)与椭圆![]() +y2=1有相同的焦点,且经过点(1,
+y2=1有相同的焦点,且经过点(1,![]() );
);
(2)经过A(2,﹣![]() ),B(﹣
),B(﹣![]() ,﹣
,﹣![]() )两点.
)两点.
18.求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,虚轴长为8,离心率为![]() ;
;
(2)与双曲线![]() =1有共同的渐近线,且过点
=1有共同的渐近线,且过点![]() .
.
19.已知抛物线C的顶点是坐标原点O,而焦点是双曲线4x2﹣y2=1的右顶点.
(1)求抛物线C的方程;
(2)若直线l:y=x﹣2与抛物线相交于A、B两点.
①求弦长|AB|;
②求证:OA⊥OB.
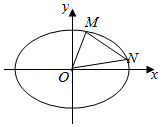
20.如图,椭圆C:x2+3y2=a2(a>0).
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若a=![]() ,M,N是椭圆C上两点,且|MN|=2
,M,N是椭圆C上两点,且|MN|=2![]() ,求△MON面积的最大值.
,求△MON面积的最大值.
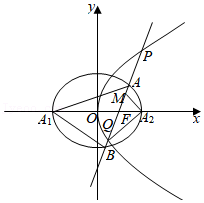
21.如图,椭圆C:![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,短轴长为2
,短轴长为2![]() ,椭圆的左、右顶点为A1、A2.过椭圆与抛物线的公共焦点F的直线l与椭圆相交于A,B两点,与抛物线E相交于P,Q两点,点M为PQ的中点.
,椭圆的左、右顶点为A1、A2.过椭圆与抛物线的公共焦点F的直线l与椭圆相交于A,B两点,与抛物线E相交于P,Q两点,点M为PQ的中点.
(1)求椭圆C和抛物线E的方程;
(2)记△ABA1的面积为S1,△MA2Q的面积为S2,若S1≥3S2,求直线l在y轴上截距的范围.
22.已知双曲线C:![]()
![]() =1(a>0,b>0),焦距为2
=1(a>0,b>0),焦距为2![]() ,渐近线方程为y=
,渐近线方程为y=![]() x.
x.
(1)求双曲线C的方程;
(2)已知M,N是双曲线C上关于x轴对称的两点,点P是C上异于M,N的任意一点,直线PM、PN分别交x轴于点T、S,试问:|OS|•|OT|是否为定值,若不是定值,说明理由,若是定值,请求出定值(其中O是坐标原点).