初中1.3 绝对值复习练习题

1.3绝对值基础

一、单选题

1．下列说法：①绝对值相等的两个数互为相反数；②绝对值等于本身的数只有正数；③不相等的两个数的绝对值不相等；④绝对值相等的两数一定相等．其中正确的个数有(      )

A．0个 B．1个 C．2个 D．3个

【答案】A

【分析】

根据①互为相反数的两个数绝对值相等；②绝对值等于一个正数的数有两个，绝对值等于0的数有一个，没有绝对值等于负数的数进行分析即可．

【详解】

解：①绝对值相等的两个数互为相反数，说法错误，正确说法应该是互为相反数的两个数绝对值相等；
②绝对值等于本身的数只有正数，说法错误，例如，0=|0|，0既不是正数也不是负数；
③不相等的两个数的绝对值不相等，说法错误，例如，2≠-2，但|2|=|-2|；
④绝对值相等的两数一定相等，说法错误，例如，|2|=|-2|，但2≠-2；
∴正确的说法有0个，
故选：A．

【点睛】

此题主要考查了绝对值，关键是掌握绝对值的性质．

2．-3的绝对值等于（   ）

A． B． C．-3 D．3

【答案】D

【分析】

根据绝对值的定义判断即可.

【详解】

|-3|=3.

故选D.

【点睛】

本题考查绝对值的概念,关键在于熟记相关基础知识.

3．下列说法中正确的是（    ）

A．0是最小的正数

B．任何有理数的绝对值都是正数

C．最大的负有理数是-1

D．如果两个数互为相反数，那么它们的绝对值相等

【答案】D

【分析】

根据正数的意义，可判断A，根据绝对值的意义，可判断B，根据负有理数的意义，可判断C，根据互为相反数的两个数的绝对值相等，可判断D．

【详解】

解：A 0不是正数，故A错误；
B  0的绝对值是0，故B错误；
C  没有最大负有理数，故C错误；
D  互为相反数的绝对值相等，故D正确；
故选：D．

【点睛】

本题考查了有理数，注意没有最大负有理数．

4．下列各数中，是负数的是（    ）

A．-（-3） B． C． D．

【答案】B

【分析】

根据相反数、绝对值的性质进行化简，然后判断.

【详解】

解：A.，不是负数；

B. ，是负数；

C. ，不是负数；

D. ，不是负数；

故选：B.

【点睛】

本题考查了相反数、绝对值的性质，有理数的分类，正确化简各数是解题的关键.

5．如果，那么对a和b的关系描述最准确的是(    )

A．互为相反数 B．相等或者互为相反数

C．a=b=0 D．以上说法均不正确

【答案】C

【分析】

由非负数的性质可得a=0、 b=0，进而可得答案．

【详解】

解：∵，∴a=0、 b=0，∴a= b=0．

故选：C．

【点睛】

本题主要考查了绝对值的意义和非负数的性质，属于基本题型，掌握非负数的性质是解题关键．

6．﹣1绝对值的相反数是（　　）

A．﹣2 B．﹣1 C．0 D．1

【答案】B

【分析】

先根据负数的绝对值是其相反数，再根据相反数的定义得出答案．

【详解】

解：﹣1的绝对值为1，

所以﹣1绝对值的相反数是﹣1，

故选：B．

【分析】

此题考查的是求一个数的绝对值和相反数，掌握绝对值的性质和相反数的定义是解决此题的关键．

7．2的相反数和绝对值分别是（    ）

A．2，2 B．-2，2 C．-2，-2 D．2，-2

【答案】B

【分析】

根据相反数和绝对值和意义求解．

【详解】

解：由相反数和绝对值的意义可以得到：

2的相反数是-2，2 的绝对值是|2|=2，

故选B ．

【点睛】

本题考查相反数和绝对值的计算，熟练掌握相反数和绝对值的意义是解题关键 ．

8．下列说法正确的有（　　）

①0减去一个数，仍得这个数；

②减去一个负数，差一定大于被减数；

③一个数的平方一定是正数；

④有理数分为正数、负数和0的三部分；

⑤一个数的相反数不可能是它本身；

⑥-2与2都是相反数；

⑦数轴上的点都表示有理数；

⑧最小的整数是0；

⑨代数式是二次三项式；

⑩单项式的系数是，次数是6

A．1个 B．2个 C．3个 D．4个

【答案】A

【分析】

根据有理数减法法则、平方的非负性、有理数的分类、相反数的性质、数轴上的点与实数的关系、多项式的定义依次进行判断即可解答．

【详解】

解：0减去一个数，等于这个数的相反数，故①错误；

减去一个负数，等于加上这个数的相反数，即等于加上一个正数，差一定大于被减数，故②正确；

一个数的平方一定是正数或0，故③错误；

有理数分为正有理数、负有理数和0的三部分，正数包括正有理数和正无理数，负数包括负有理数和负无理数，故④错误；

0的相反数是0，等于它本身，故⑤错误；

-2是2的相反数，相反数要成对出现，不能单独说-2是相反数，故⑥错误；

有理数可以用数轴上的点来表示，但数轴上的点不都表示有理数，也可以表示无理数，故⑦错误；

没有最小的整数，故⑧错误；

代数式不是整式，也就不能叫做二次三项式，故⑨错误；

单项式的系数是，次数是5，故⑩错误

故选：A

【点睛】

本题主要考查有理数减法法则、平方的非负性、有理数的分类、相反数的性质、数轴上的点与实数的关系、多项式的定义，熟练掌握各个定义和法则是解答本题的关键．

二、填空题

9．如果，则_____

【答案】±7

【详解】

试题分析：因为，所以±7.

考点：绝对值.

10．绝对值是5的有理数是_____．

【答案】±5

【详解】

分析：根据绝对值得定义：“在数轴上，表示一个数a的点到原点的距离叫做这个数的绝对值”求解即可.

详解：∵-5和5到原点的距离都等于5，

∴绝对值是5的有理数是±5.

点睛：本题考查了绝对值得意义，题目比较简单，熟练掌握绝对值定义是解答本题的关键.

11．若|5﹣x|＝1，则x＝_____．

【答案】4或6

【分析】

根据绝对值的定义得到5﹣x＝±1，解方程即可得到结论．

【详解】

解：∵|5﹣x|＝1，

∴5﹣x＝1或5﹣x＝-1

∴x＝4或6，

故答案为：4或6．

【解答】

本题考查了绝对值的意义和解一元一次方程等知识，将绝对值方程化为两个一元一次方程是解题关键．

12．点A表示3，在数轴上与点A距离6个单位长度的点表示的数为_______．

【答案】-3或9

【分析】

根据数轴上的两点之间的距离的计算方法，可以列出绝对值的方程，通过解方程求解即可．

【详解】

设这个数为，

由题意得：，

∴或，

解得：或，

故答案为：-3或9．

【点睛】

本题考查数轴表示数、绝对值以及方程的意义和解法，明确数轴上两点之间距离的计算方法是解题的关键．

13．相反数是本身的数___________，绝对值是本身的数___________．

【答案】0    非负数   

【详解】

解：因为正数的相反数是负数，0的相反数是它本身（0），负数的相反数是正数，

所以相反数是本身的数是0；

因为正数的绝对值是它本身，0的绝对值为0，负数的绝对值是它的相反数，

所以绝对值是本身的数是正数和0，即非负数．

故答案是：0， 非负数．

14．若有理数a是一个负数，则式子|a|+a的结果为_____．

【答案】0

【分析】

根据题意条件对原式化简即可得出结论．

【详解】

是一个负数，

，
故答案为：0．

【点睛】

本题考查绝对值化简计算问题，熟练掌握绝对值的代数意义是解题关键．

15．在数－0.34，，0.3，－35%，，中，最大的数是__________，最小的数是_________．

【答案】，    -35%   

【解析】

【分析】

先把给出的数都化为小数，再根据正数大于一切负数，两个负数比较大小，绝对值大的反而小，即可得出答案.

【详解】

，，，

最大的数是：，最小的数是.

故答案为：；.

【点睛】

此题考查了有理数的大小，解决有关小数、百分数、分数之间的大小比较，一般把分数、百分数化为小数再进行比较，从而解决问题.

16．若|x|=，则实数x=______．

【答案】±

【分析】

当a＞0时，绝对值等于a的数有两个，它们分别位于原点的两侧，且到原点的距离相等．

【详解】

解：在数轴上到原点的距离为的数有两个，它们是±．

故答案为：±．

【点睛】

本题主要考查的是绝对值的定义，掌握绝对值的定义是解题的关键．

三、解答题

17．已知求的值．

【答案】1或−3

【分析】

由已知可求a＝3或a＝−1，代入所求式子即可．

【详解】

∵|a−1|＝2，

∴a＝3或a＝−1，

当a＝3时，−3＋|1＋a|＝−3＋4＝1；

当a＝−1时，−3＋|1＋a|＝−3；

综上所述，所求式子的值为1或−3．

【点睛】

本题考查绝对值的性质；熟练掌握绝对值的性质，能够准确的去掉绝对值符号进行运算是解题的关键．

18．画一条数轴，把下列各数在数轴上表示出来，并用“＜”把它们连接起来．            

－4，  3.5，  0，， 2

【答案】-4＜＜0＜2＜3.5

【解析】

【分析】

根据数轴是表示数的一条直线，可把数在数轴上表示出来，根据数轴上的点表示的数右边的总比左边的大，可得答案；

【详解】

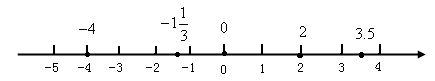
-4＜＜0＜2＜3.5．

【点睛】

本题考查了有理数大小比较，数轴上的点表示的数右边的总比左边的大．

19．已知a32与互为相反数，求式子a2b2的值．

【答案】25．

【分析】

利用相反数与非负数的性质：两个非负数之和为0，则它们都为0，即由可得，从而得到答案．

【详解】

由题意知：

∴，即：

∴

【点睛】

本题考查相反数与非负数，掌握相反数与非负数的性质是解题的关键．

20．把数 在数轴上表示出来，然后用“>”把它们连接起来.

【答案】在数轴上表示见解析, ．

【分析】

先把各个数在数轴上表示出来，再根据在数轴上的位置进行比较即可求出答案．

【详解】

解：把数在数轴上表示出来如下：

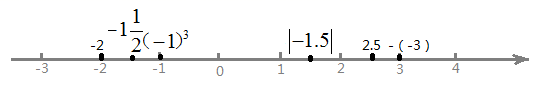
用“>”把它们连接起来： ．

【点睛】

本题考查利用数轴比较有理数的大小，相反数，绝对值等知识点，熟记有理数的大小比较法则是解题的关键，注意：在数轴上表示的数，右边的数总比左边的数大．

21．出租车司机小李某天下午在东西方向的公路上载运客人，如果规定向东为正，向西为负，出发地记为点.出租车的行程如下（单位：千米）：.

（1）最后一名客人到达目的地时，小李距出车地点的距离是多少?

（2）若汽车耗油量为升/千米，那么这天下午汽车共耗油多少升？

【答案】（1）4千米；（2）10.08升．

【分析】

（1）求出各数之和，根据计算结果判断即可；

（2）求出各数绝对值之和，得出行驶里程，再乘以0.12即可得到结果．

【详解】

解：（1）根据题意得：：

（＋12）＋（−7）＋（＋10）＋（−13）＋（−11）＋（＋4）＋（−13）＋（＋14）＝−4（千米），

故最后一名客人到达目的地时，小李距出车地点的距离4千米；

（2）这天下午行驶总里程为：|＋12|＋|−7|＋|＋10|＋|−13|＋|−11|＋|＋4|＋|−13|＋|＋14|＝84（千米），

则共耗油量为：84×0.12＝10.08（升）；

所以这天下午汽车共耗油10.08升．

【点睛】

本题考查了正数和负数，利用绝对值的意义求出行驶里程是解答此题的关键．

22．已知，求(a＋b)2019＋b2020的值

【答案】0.

【分析】

利用绝对值的非负性可求出a、b的值，再代入即可.

【详解】

解：∵|a+2|≥0，(b﹣1)2≥0

又∵|a+2|+(b﹣1)2＝0

∴|a+2|＝0且(b﹣1)2＝0

∴a+2＝0且b﹣1＝0

∴a＝－2且b=1

∴原式=(－2+1)2019+12020

=－1+1

=0

【点睛】

此题考查的是绝对值的非负性和有理数的乘方运算.

23．某体育用品公司生产了一批比赛用的篮球，比赛用的篮球质量有严格规定，其中误差符合要求，现质检员从中抽取6个篮球进行检查，检查结果如下表：

（1）有几个篮球符合质量要求？（2）其中质量最接近标准的是几号球？

【答案】（1）有5个篮球符合质量要求；（2）⑤号球的质量最接近标准质量．

【解析】

【分析】

（1）根据绝对值的性质即可求解；

（2）根据绝对值的性质即可求解.

【详解】

解：（1），，，，，，

只有第④个球的质量绝对值大于，不符合质量要求，其他都符合，

所以有5个篮球符合质量要求．

（2）因为，绝对值最小，所以⑤号球的质量最接近标准质量．

【点睛】

此题主要考查绝对值的应用，解题的关键是熟知绝对值的性质与应用.

24．某同学学习编程后，编了一个关于绝对值的程序，当输入一个数值后，屏幕输出的结果总比该数的绝对值小1.某同学输入－7后，把输出的结果再次输入，则最后屏幕输出的结果是多少？

【答案】5.

【分析】

根据绝对值的代数意义和已知条件进行分析解答即可.

【详解】

∵|－7|－1＝6，|6|－1＝5，

∴最后屏幕输出的结果为5.

【点睛】

熟知“绝对值的代数意义：一个正数的绝对值是它本身，0的绝对值是0，负数的绝对值是它的相反数”是解答本题的关键.

25．求下列各数的绝对值：12， ，－7.5， 0

【答案】|12|＝12；＝ ， |－7.5|＝7.5，|0|＝0

【详解】

略