第3章 实数（知识清单）-（浙教版）

第3章 实数知识清单

一、平方根和算术平方根的概念

1.算术平方根的定义

如果一个正数的平方等于，即,那么这个正数叫做的算术平方根（规定0的算术平方根还是0）；的算术平方根记作，读作“的算术平方根”，叫做被开方数.

要点：当式子有意义时，一定表示一个非负数，即≥0，≥0.

2.平方根的定义

　  如果，那么叫做的平方根.求一个数的平方根的运算，叫做开平方.平方与开平方互为逆运算. (≥0)的平方根的符号表达为，其中是的算术平方根.

二、平方根和算术平方根的区别与联系

1．区别：（1）定义不同；（2）结果不同：和

2．联系：（1）平方根包含算术平方根；

（2）被开方数都是非负数；

        （3）0的平方根和算术平方根均为0．

要点：（1）正数的平方根有两个，它们互为相反数，其中正的那个叫它的算术平方根；负数没有平方根．

（2）正数的两个平方根互为相反数，根据它的算术平方根可以立即写出它的另一个平方根.因此，我们可以利用算术平方根来研究平方根.

三、平方根的性质

四、平方根小数点位数移动规律

被开方数的小数点向右或者向左移动2位，它的算术平方根的小数点就相应地向右或者向左移动1位.例如：，，，.

五、有理数与无理数

有限小数和无限循环小数都称为有理数.无限不循环小数又叫无理数.

要点：（1）无理数的特征：无理数的小数部分位数无限.无理数的小数部分不循环，不能表示成分数的形式.

       （2）常见的无理数有三种形式：①含类.②看似循环而实质不循环的数，如：1.313113111…….③带有根号的数，但根号下的数字开方开不尽，如.

六、实数

有理数和无理数统称为实数.

1.实数的分类

按定义分：

    实数

按与0的大小关系分：

    实数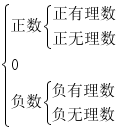

 2.实数与数轴上的点的关系

我们尝试用数轴上的一个点来表示．

由前面的学习，我们知道两个边长为1的小正方形可以拼成一个面积为2的正方形ABCD，它的边长为．观察正方形ABCD，可知它的一边是一个直角三角形的斜边，这个直角三角形的两条直角边长都是1．

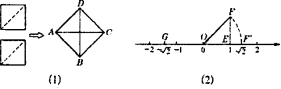
这样，就在数轴上确定一个点来表示．

要点：每一个实数都可以用数轴上的点表示，而且这些点是唯一的；反过来，数轴上的每一个点都表示一个实数．数轴上的点与实数一一对应。

3.两个实数比较大小

①负数小于0,0小于正数；两个正数绝对值大的数较大，两个负数绝对值大的数较小；从数轴上看，右边的点表示的数比左边的大。

②数轴上，如果点A,点B所对应的数分别为a，b，那么A,B两点的距离

4.估算：怎样估算无理数 (①误差小于1)？(②误差小于0.1)？

误差小于0.1就是指估算出来的值与准确值之间的差的绝对值小于0.1.

估算无理数的方法是： 

（1）通过平方运算，采用“夹逼法”，确定真正值所在范围；

（2）根据问题中误差允许的范围内取出近似值。

（3）“精确到”与“误差小于”意义不同。如精确到1m是四舍五入到个位，答案惟一；误差小于1m，答案在真正值左右1m都符合题意，答案不惟一。在本章中误差小于1m就是估算到个位，误差小于10m就是估算到十位。

记忆常用数的近似值：≈1.414   ≈1.732   ≈2.236

七、立方根的定义

如果一个数的立方等于，那么这个数叫做的立方根或三次方根.这就是说，如果，那么叫做的立方根.求一个数的立方根的运算，叫做开立方.

要点：一个数的立方根，用表示，其中是被开方数，3是根指数. 开立方和立方互为逆运算.

八、立方根的特征

立方根的特征：正数的立方根是正数，负数的立方根是负数，0的立方根是0.

要点：任何数都有立方根，一个数的立方根有且只有一个，并且它的符号与这个非零数的符号相同. 两个互为相反数的数的立方根也互为相反数.

九、立方根的性质

要点：第一个公式可以将求负数的立方根的问题转化为求正数的立方根的问题.

十、立方根小数点位数移动规律

被开方数的小数点向右或者向左移动3位，它的立方根的小数点就相应地向右或者向左移动1位.例如，，，，.

十一、实数的运算

有理数关于相反数和绝对值的意义同样适合于实数.

当数从有理数扩充到实数以后，实数之间不仅可以进行加、减、乘、除（除数不为0）、乘方运算，而且正数及0可以进行开平方运算，任意一个实数可以进行开立方运算.在进行实数的运算时，有理数的运算法则及运算性质等同样适用.