培优专题01 与三角形模型有关的角度计算-2023-2024学年八年级数学上册精选专题培优讲与练（人教版）

这是一份培优专题01 与三角形模型有关的角度计算-2023-2024学年八年级数学上册精选专题培优讲与练（人教版），文件包含培优专题01与三角形模型有关的角度计算-原卷版docx、培优专题01与三角形模型有关的角度计算-解析版docx等2份试卷配套教学资源，其中试卷共61页， 欢迎下载使用。

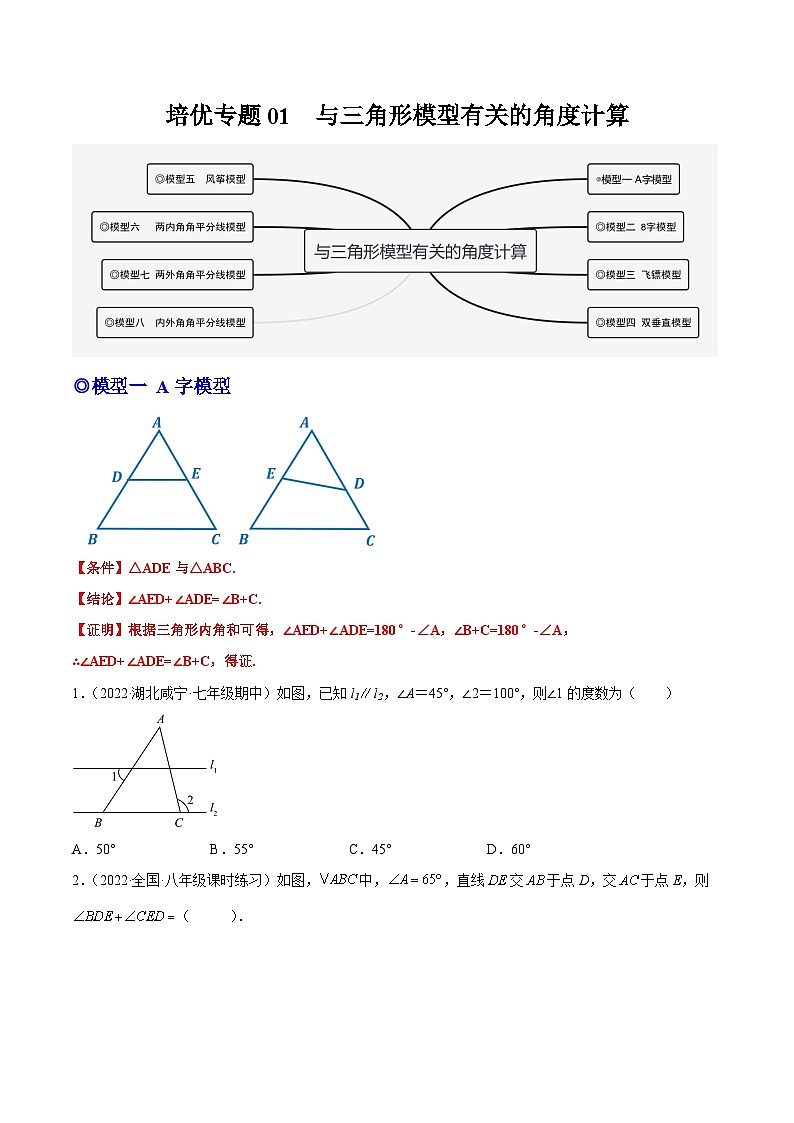
培优专题01 与三角形模型有关的角度计算

◎模型一 A字模型

【条件】△ADE与△ABC.
【结论】∠AED+∠ADE=∠B+C.
【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，
∴∠AED+∠ADE=∠B+C，得证.
1．（2022·湖北咸宁·七年级期中）如图，已知l1l2，∠A＝45°，∠2＝100°，则∠1的度数为（　　）

A．50° B．55° C．45° D．60°
【答案】B
【分析】根据平角的定义得出∠ACB＝80°，根据三角形内角和得到∠ABC＝55°，再根据平行线的性质即可得解．
【详解】解：∵∠2＝100°，
∴∠ACB＝180°−100°＝80°，
∵∠A＝45°，
∴∠ABC＝180°−45°−80°＝55°，
∵l1l2，
∴∠1＝∠ABC＝55°，
故选：B．
【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”是解题的关键．
2．（2022·全国·八年级课时练习）如图，中，，直线交于点D，交于点E，则（       ）．

A． B． C． D．
【答案】D
【分析】根据三角形内角和定理求出，根据平角的概念计算即可．
【详解】解：，
，
，
故选：D．
【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于是解题的关键．
3．（2022·全国·八年级课时练习）如图是某建筑工地上的人字架，若，那么的度数为_________．

【答案】
【分析】根据平角的定义求出，再利用三角形的外角的性质即可解决问题．
【详解】解：如图

，，
，
，
，
故答案为：．
【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．
4．（2020·湖南·常德市第二中学九年级期中）如图，在中，，，，分别在、上，将沿折叠，使点落在点处，若为的中点，则折痕的长为__．

【答案】2
【分析】由折叠的特点可知，，又，则由同位角相等两直线平行易证，故，又为的中点可得，由相似的性质可得．
【详解】解：沿折叠，使点落在点处，
，，
，
又为的中点，AE=AE'
∴AE:AC=1:3
，
即，
．
故答案为：2．
【点睛】本题考查相似三角形的判定和性质，掌握“A”字形三角形相似的判定和性质为解题关键．
5．（2022·全国·八年级课时练习）如图所示，的两边上各有一点，连接，求证．

【答案】见解析
【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可．
【详解】解：和是的外角，
．
又，
．
【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．
◎模型二 8字模型

【条件】AD、BC相交于点O.
【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)
【证明】在△ABO中，由内角和定理：∠A+∠B+∠BOA=180°，在△CDO中，∠C+∠D+∠COD=180°，
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD
∴∠A+∠B=∠C+∠D，得证.
6．（2022·全国·八年级课时练习）如图，AB和CD相交于点O，∠A＝∠C，则下列结论中不能完全确定正确的是（       ）

A．∠B＝∠D B．∠1＝∠A＋∠D C．∠2＞∠D D．∠C＝∠D
【答案】D
【分析】利用三角形的外角性质，对顶角相等逐一判断即可．
【详解】∵∠A＋∠AOD＋∠D＝180°，∠C＋∠COB＋∠B＝180°，∠A＝∠C，∠AOD＝∠BOC，
∴∠B＝∠D，
∵∠1＝∠2＝∠A＋∠D，
∴∠2＞∠D，
故选项A，B，C正确，
故选D．
【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键．
7．（2022·全国·八年级课时练习）如图，∠1=60°，则∠A+∠B+∠C+∠D+∠E+∠F=（　　）

A．240° B．280° C．360° D．540°
【答案】A
【分析】根据三角形内角和定理得到∠B与∠C的和，然后在五星中求得∠1与另外四个角的和，加在一起即可．
【详解】解：由三角形外角的性质得：∠3=∠A+∠E，∠2=∠F+∠D，
∵∠1+∠2+∠3=180°，∠1=60°，
∴∠2+∠3=120°，
即：∠A+∠E+∠F+∠D=120°，
∵∠B+∠C=120°，
∴∠A+∠B+∠C+∠D+∠E+∠F=240°．
故选A．

【点睛】本题考查了三角形的外角和三角形的内角和的相关知识，解决本题的关键是将题目中的六个角分成两部分来分别求出来，然后再加在一起．
8．（2022·全国·八年级课时练习）如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I＝__．

【答案】900°
【分析】根据多边形的内角和，可得答案．
【详解】解：连EF，GI，如图
，
∵6边形ABCDEFK的内角和＝（6－2）×180°＝720°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝720°－（∠1＋∠2），
即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋（∠1＋∠2）＝720°，
∵∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F∠H＋（∠3＋∠4）＝900°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F（∠3＋∠4）＋∠5＋∠6＋∠H＝720°＋180°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＝900°，
故答案为：900°．
【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．
9．（2022·全国·八年级课时练习）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为__．

【答案】1080°
【分析】连KF，GI，根据n边形的内角和定理得到7边形ABCDEFK的内角和＝（7－2）×180°＝900°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，由三角形内角和定理可得到∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，即可得到∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数．
【详解】解：连KF，GI，如图，

∵7边形ABCDEFK的内角和＝（7－2）×180°＝900°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＝900°－（∠1＋∠2），
即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，
∵∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＝900°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K＝1080°．
故∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数为1080°．
故答案为：1080°．
【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．
10．（2022·全国·八年级课时练习）如图，OAB和OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M

（1）如图1，当α＝90°时，∠AMD的度数为 °；
（2）如图2，当α＝60°时，求∠AMD的度数；
（3）如图3，当OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用α表示∠AMD，并用图3进行证明；若不确定，说明理由．
【答案】（1）；（2）；（3）
【分析】（1）如图1，设交于，只要证明，推出，由，可得；
（2）如图2，设交于，只要证明，推出，由，可得；
（3）如图3，设交于，只要证明，推出，由，可得，可得；
【详解】解：（1）如图1中，设交于

∵，
∴
∴
∴
∵
∴
∴
故答案为
（2）如图2，设交于，

∵，
∴
∴
∴
∵
∴
∴
故答案为
（3）如图3，设交于，

∵，
∴
∴
∴
∵
∴
∴
故答案为
【点睛】本题考查了几何变换综合题，全等三角形的判定，三角形内角和性质，解题的关键是灵活运用所学知识解决问题，学会利用“8字型”证明角相等．

◎模型三 飞镖模型

【条件】四边形ABDC如上左图所示.
【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)
【证明】如上右图，连接AD并延长到E，则：
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.
11．（2022·全国·八年级课时练习）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果，，那么的度数是（       ）．

A． B． C． D．
【答案】A
【分析】延长BE交CF的延长线于O，连接AO，根据三角形内角和定理求出再利用邻补角的性质求出，再根据四边形的内角和求出，根据邻补角的性质即可求出的度数．
【详解】延长BE交CF的延长线于O，连接AO，如图，

∵
∴
同理得
∵
∴


∵
∴
∴

∴,
故选：A．
【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：．
12．（2022·全国·八年级课时练习）如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（　　）

A．115° B．120° C．125° D．130°
【答案】D
【详解】∵BE为△ABC的高，∠BAC=50°，
∴∠ABE=90°-50°=40°，
∵CF为△ABC的高，
∴∠BFC=90°，
∴∠BHC=∠ABE+∠BFC=40°+90°=130°．
故选D．
13．（2022·全国·八年级课时练习）如图，若，则____________．

【答案】230°
【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．
【详解】解：如图

∵∠EOC=∠E+∠2=115°，∠2=∠D+∠C，
∴∠E+∠D+∠C=115°，
∵∠EOC=∠1+∠F=115°，∠1=∠A+∠B，
∴∠A+∠B+∠F=115°，
∴∠A+∠B+∠C+∠D+∠E+∠F=230°，
故答案为：230°．
【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．
14．（2022·山东德州·七年级期末）如图，则∠A+∠B+∠C+∠D+∠E的度数是__．

【答案】180°
【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠4＝∠A＋∠2，∠2＝∠D＋∠C，进而利用三角形的内角和定理求解．
【详解】解：如图可知：

∵∠4是三角形的外角，
∴∠4＝∠A＋∠2，
同理∠2也是三角形的外角，
∴∠2＝∠D＋∠C，
在△BEG中，∵∠B＋∠E＋∠4＝180°，
∴∠B＋∠E＋∠A＋∠D＋∠C＝180°．
故答案为：180°．
【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．
15．（2022·全国·八年级课时练习）模型规律：如图1，延长交于点D，则．因为凹四边形形似箭头，其四角具有“”这个规律，所以我们把这个模型叫做“箭头四角形”．

模型应用
（1）直接应用：
①如图2，，则__________；
②如图3，__________；
（2）拓展应用：
①如图4，、的2等分线（即角平分线）、交于点，已知，，则__________；
②如图5，、分别为、的10等分线．它们的交点从上到下依次为、、、…、．已知，，则__________；
③如图6，、的角平分线、交于点D，已知，则__________；
④如图7，、的角平分线、交于点D，则、、之同的数量关系为__________．
【答案】（1）①110；②260；（2）①85；②99；③142；④∠B-∠C+2∠D=0
【分析】（1）①根据题干中的等式直接计算即可；
②同理可得∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE，代入计算即可；
（2）①同理可得∠BO1C=∠BOC-∠OBO1-∠OCO1，代入计算可得；
②同理可得∠BO7C=∠BOC-（∠BOC-∠A），代入计算即可；
③利用∠ADB=180°-（∠ABD+∠BAD）=180°-（∠BOC-∠C）计算可得；
④根据两个凹四边形ABOD和ABOC得到两个等式，联立可得结论．
【详解】解：（1）①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；
②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°；

（2）①∠BO1C=∠BOC-∠OBO1-∠OCO1
=∠BOC-（∠ABO+∠ACO）
=∠BOC-（∠BOC-∠A）
=∠BOC-（120°-50°）
=120°-35°
=85°；
②∠BO7C=∠BOC-（∠BOC-∠A）
=120°-（120°-50°）
=120°-21°
=99°；
③∠ADB=180°-（∠ABD+∠BAD）
=180°-（∠BOC-∠C）
=180°-（120°-44°）
=142°；
④∠BOD=∠BOC=∠B+∠D+∠BAC，
∠BOC=∠B+∠C+∠BAC，
联立得：∠B-∠C+2∠D=0．
【点睛】本题主要考查了新定义—箭头四角形，利用了三角形外角的性质，还考查了角平分线的定义，图形类规律，解题的关键是理解箭头四角形，并能熟练运用其性质．

◎模型四 双垂直模型

【条件】∠B=∠D=∠ACE=90°.
【结论】∠BAC=∠DCE，∠ACB=∠CED.
【证明】∵∠B=∠D=∠ACE=90°；∴∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∴∠BAC=∠DCE
同理,∠ACB+∠DCE =90°，且∠CED+∠DCE =90°；∴∠ACB=∠CED，得证.
16．（2021·青海海东·八年级期中）如图，已知△ABC≌△CDE，∠B＝90°，点C为线段BD上一点，则∠ACE的度数为（       ）

A．94° B．92° C．90° D．88°
【答案】C
【分析】由全等三角形的性质得出∠ACB＝∠CED，则可得出答案．
【详解】解：∵△ABC≌△CDE，

∴∠ACB＝∠CED，∠B＝∠D＝90°，
∵∠CED+∠ECD＝90°，
∴∠ACB+∠ECD＝90°，
∵∠ACB+∠ECD+∠ACE＝180°，
∴∠ACE＝90°．
故选：C．
【点睛】本题考查了全等三角形的性质；熟练掌握三角形全等的性质定理是解题的关键．
17．（2020·河南·郑州市第八中学模拟预测）如图所示，一副三角尺摆放置在矩形纸片的内部，三角形的三个顶点恰好在矩形的边上，若，则等于（　）

A． B． C． D．
【答案】D
【分析】根据矩形的性质可得∠C=90°，AD∥BC，利用直角三角形的两个锐角互余求出∠GFC，从而求出∠EFB，然后根据平行线的性质可得∠AEF＋∠EFB=180°，从而求出结论．
【详解】解：∵四边形ABCD为矩形
∴∠C=90°，AD∥BC
∵
∴∠GFC=90°－∠FGC=74°
由三角尺可知：∠EFG=60°
∴∠EFB=180°－∠GFC－∠EFG=46°
∵AD∥BC
∴∠AEF＋∠EFB=180°
∴∠AEF=180°－∠EFB=134°
故选D．
【点睛】此题考查的是矩形的性质、直角三角形的性质和平行线的性质，掌握矩形的性质、直角三角形的两个锐角互余和平行线的性质是解决此题的关键．
18．（2022·山东青岛·七年级期末）如图，小虎用10块高度都是的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（，），点在上，点和分别与木墙的顶端重合，则两堵木墙之间的距离为______．

【答案】40 cm
【分析】根据题意可得AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE＝∠DAC，再证明△ADC≌△CEB即可，利用全等三角形的性质进行解答．
【详解】解：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，
∴∠ADC＝∠CEB＝90°，
∴∠ACD＋∠BCE＝90°，∠ACD＋∠DAC＝90°，
∴∠BCE＝∠DAC，
在△ADC和△CEB中，
，
∴△ADC≌△CEB（AAS）；
由题意得：AD＝EC＝12cm，DC＝BE＝28cm，
∴DE＝DC＋CE＝40（cm），
答：两堵木墙之间的距离为40cm，
故答案为：40 cm．
【点睛】此题主要考查了全等三角形的应用，涉及到垂直的定义、直角三角形的性质和连个三角形全等的判定与性质等知识点，解题的关键是正确找出证明三角形全等的条件．
19．（2021·江苏盐城·七年级期中）将含有角的直角三角板（）和直尺按如图方式摆放，已知，则______．

【答案】24
【分析】过点B作BC//MN，由平行线传递性，可得BC//KL，再由平行线的性质可得 ， ，最后由在直角三角形中两锐角互余的关系，求出 ．
【详解】解：过点B作BC//MN，如图所示：

MN//KH
BC//KL

又

又 BC//MN

又

又


故答案为：24
【点睛】本题考查了平行线的判定与性质(两直线平行，内错角相等)，平行线传递性(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)，直角三角形中两锐角互余，角的和差计算等综合知识点．难点是作已知直线的平行线．
20．（2022·全国·八年级专题练习）如图1，已知中，，，、分别与过点的直线垂直，且垂足分别为E，D．


(1)猜想线段AD、、三者之间的数量关系，并给予证明．
(2)如图2，当过点C的直线绕点旋转到的内部，其他条件不变，如图2所示，
①线段AD、、三者之间的数量关系是否发生改变？若改变，请直接写出三者之间的数量关系，若不改变，请说明理由；
②若，时，求的长．
【答案】(1)，证明见解析
(2)①发生改变，；②1.3
【分析】（1）证明，可得，CD＝BE， 即可求解；
（2）①证明，可得，CD＝BE， 即可求解；②由①可得，从而得到，即可求解．
（1）
解：，   理由如下：
∵、分别与过点的直线垂直，
∴，
∴，
∵，
∴，
∴，
在和中，，
，
，CD＝BE，
∵ DE＝EC＋CD，     
；
（2）
解：①发生改变．
∵、分别与过点的直线垂直，
∴，
∴，
∵，
∴，
∴，
在和中，，
，
，CD＝BE，
∵ DE＝CE-CD，       
∴；
②由①知：，
∴，
∴BE的长为1.3.
【点睛】本题主要考查了全等三角形的判定和性质、等角的余角相等，熟练掌握全等三角形的判定和性质是解题的关键．

◎模型五 风筝模型

【条件】四边形ABPC，分别延长AB、AC于点D、E，如上左图所示.
【结论】∠PBD+∠PCE=∠A+∠P.
【证明】如上右图，连接AP，则：∠PBD=∠PAB+∠APB，∠PCE=∠PAC+∠APC，
∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC，得证.
21．（2022·内蒙古赤峰·八年级期末）如图，将的一角折叠，若，则（       ）

A．50° B．65° C．115° D．130°
【答案】C
【分析】根据折叠性质证得∠3=∠4，∠5=∠6，再根据平角定义求得∠4+∠5=115°，然后根据三角形的内角和定理求解即可．
【详解】解：如图，

由折叠性质得：∠3=∠4，∠5=∠6，
∵∠1+∠3+∠4=180°，∠5+∠6+∠2=180°，
∴∠1+∠2+2∠4+2∠5=360°，
∵∠1+∠2=130°，
∴2∠4+2∠5=360°－130°=230°，
∴∠4+∠5=115°，
∵∠4+∠5+∠A=180°，∠A+∠B+∠C=180°，
∴∠B+∠C=∠4+∠5=115°，
故选：C．
【点睛】本题考查三角形折叠中的角度问题，熟练掌握折叠性质是解答的关键.
22．（2022·海南海口·七年级期末）如图，把△ABC纸片沿MN折叠，使点C落在△ABC内部点C′处，若∠C=36°，则∠1+∠2等于（       ）

A．54° B．62° C．72° D．76°
【答案】C
【分析】根据折叠可知∠C=∠，四边形内角和为360°，即可求出+，用平角的定义即可求出∠1+∠2
【详解】∵△CMN折叠得到
∴∠C=∠
∵∠1=180°-，∠2=180°-
∴∠1+∠2=180°-+180°-=360°-（+）
∵+=360°-∠C-=360°-36°-36°=288°
∴∠1+∠2=360°-288°=72°
故选：C
【点睛】本题主要考查了折叠问题，掌握三角形的内角和定理，四边形的内角和以及平角的定义是解题的关键．
23．（2022·山东烟台·七年级期中）如图，在三角形纸片ABC中，，将纸片的一角折叠，使点C落在△ABC内，若，则∠2的度数为_________.


【答案】30°##30度
【分析】根据题意，已知∠A=65°，∠B=75°，可结合三角形内角和定理和四边形内角和求解．
【详解】解：如图，设折痕为DE；
∵，，
∴，
∴，
又∵，
∴，
故答案为：30°．


【点睛】本题主要是考查了三角形、四边形内角和，即三角形的内角和为180°，四边形的内角和为360°；熟练掌握三角形的内角和定理是解题的关键．
24．（2022·湖北恩施·一模）图，把等边沿直线折叠，点落在处，若，则______．


【答案】
【分析】先求出的度数，再根据折叠得到，即可求出的度数．
【详解】∵等边沿直线折叠
∴，
∵
∴
∴
∴
故答案为：
【点睛】此题考查翻折问题，折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．

25．（2022·江苏·扬州市竹西中学七年级期末）如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A＝∠1+∠2．请你继续探索：


(1)如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图②，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．
(2)如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）
【答案】(1)∠1﹣∠2＝2∠A，理由见解析
(2)∠A+∠D＝180°+（∠1+∠2），理由见解析
【分析】（1）连接，根据三角形的外角的性质以及轴对称的性质进行分析；
（2）根据平角的定义以及四边形的内角和定理进行计算即可．
（1）解：如图所示，连接，
∵，；∴∠1﹣∠2＝2∠A；
（2）解：由图形折叠的性质可知，，则，即，所以，∠1+∠2＝2（∠A+∠D）﹣360°，即．
【点睛】本题考查了折叠的性质，三角形的外角的性质及多边形内角和，解题的关键掌握这些知识点．

◎模型六 两内角角平分线模型

【条件】△ABC中，BI、CI分别是∠ABC和∠ACB的角平分线，且相交于点I.
【结论】
【证明】∵BI是∠ABC平分线，∴∵CI是∠ACB平分线，∴
由A→B→I→C→A的飞镖模型可知：
∠I=∠A+∠2+∠3=∠A++=∠A+=.
26．（2022·山东东营·七年级期末）如图，在△ABC中，BF平分∠ABC，CF平分∠ACB，∠BFC=125°，则∠A的度数为（　　）

A．60° B．80° C．70° D．45°
【答案】C
【分析】先根据三角形内角和定理得出的度数，再由角平分线的性质得出的度数，根据三角形内角和定理即可得出结论．
【详解】解：∵，
∴．
∵平分，平分，
∴，
∵，
∴．
故选：C．
【点睛】本题考查的是三角形内角和定理，以及三角形角平分线的定义，熟知三角形内角和是180°是解答此题的关键．
27．（2022·福建·泉州五中七年级期末）如图，在四边形ABCD中，∠A+∠D＝α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P＝（       ）

A．90°﹣α B．α C．90°+α D．360°﹣α
【答案】B
【分析】先求出∠ABC＋∠BCD的度数，然后根据角平分线的定义以及三角形的内角和定理求∠P的度数．
【详解】解：在四边形ABCD中，∠ABC＋∠BCD＝360°−（∠A＋∠D）＝360°−α，
∵BP和CP分别为∠ABC、∠BCD的平分线，
∴∠PBC＋∠PCB＝∠ABC＋∠BCD＝（∠ABC＋∠BCD）＝（360°−α）＝180°−α，
∴∠P＝180°−（∠PBC＋∠PCB）＝180°−（180°−α）＝α．
故选：B．
【点睛】本题考查了多边形的内角和以及三角形的内角和定理，关键是先求出∠ABC＋∠BCD的度数．
28．（2022·河南鹤壁·七年级期末）已知中，．在图1中、的平分线交于点，则可计算得；在图2中，设、的两条三等分角线分别对应交于、，则_______________．

【答案】
【分析】首先根据三角形内角和定理求得，再由三等分角线可得，由三角形内角和定理即可求得．
【详解】解：，
，
、的两条三等分角线分别对应交于、，
，
，
故答案为：．
【点睛】本题考查三角形内角和定理，解题的关键是熟练运用三等分角线求解．
29．（2022·江苏常州·七年级期中）如图，在△MBC中，∠ABC、∠ACB的角平分线OB、OC交于点O，若∠O=m°，则∠A的度数是______________________________°（用含m的代数式表示）．

【答案】（2m-180）
【分析】先由角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，再利用三角形内角和定理求解即可．
【详解】解：∵OB，OC分别是∠ABC和∠ACB的角平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∵∠O+∠OBC+∠OCB=180°，
∴∠OBC+∠OCB=180°-∠O=180°-m°，
∴∠ABC+∠ACB=2∠OBC+2∠OCB=360°-2m°，
∴∠A=180°-∠ABC-∠ACB=2m°-180°，
故答案为：（2m-180）．
【点睛】本题主要考查了三角形内角和定理，角平分线的定义，熟知相关知识是解题的关键．

30．（2021·重庆·垫江第八中学校七年级阶段练习）在△ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN⊥BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．


(1)如图1，若∠A=110°，∠BEC=130°，则∠2= °，∠3－∠1= °；
(2)如图2，猜想∠3－∠1与∠A的数量关系，并证明你的结论；
(3)若∠BEC=，∠BDC=，用含和的代数式表示∠3－∠1的度数．（直接写出结果即可）
【答案】(1)20；55；
(2)，证明见解析
(3)
【分析】（1）根据三角形外角的性质即可求出∠ACE的度数，根据角平分线的定义即可求出∠2的度数，进而求出∠3的度数，∠ACB的度数，利用三角形内角和定理和角平分线的定义求出∠1的度数即可得到答案；
（2）根据角平分线的定义得到，再根据三角形内角和定理表示出∠3．然后推出∠3-∠1=90°-∠1-∠2，再根据三角形内角和定理求解即可；
（3）在△BCE和△BCD中根据三角形内角和定理得到∠1+∠2，再根据（2）中结论求解即可；
（1）
解：∵∠A=110°，∠BEC=130°，
∴∠ACE=∠BEC-∠A=20°，
∵CE平分∠ACB，
∴∠2=∠ACE=20°，∠ACB=40°，
∴∠ABC=180°-∠A-∠ACB=30°，
∵BD平分∠ABD，
∴，
∵MN⊥BC，即∠MNC=90°，
∴∠3=180°-∠2-∠MNC=70°，
∴∠3-∠1=55°，
故答案为：20；55；
（2）
解：，证明如下：
∵在△ABC中，BD，CE是它的两条角平分线，
∴，
∵MN⊥BC，即∠MNC=90°，
∴∠3=180°-∠MNC-∠2=90°-∠2，
∴∠3-∠1=90°-∠1-∠2，
∵∠ABC+∠ACB=180°-∠A，
∴，即，
∴；
（3）
解：∵在△ABC中，BD，CE是它的两条角平分线，
∴，
∵∠1+∠BCD+∠BDC=180°，∠2+∠BEC+∠EBC=180°，
∴，
∴，
由（2）得，
∴，
∴，
∴．
【点睛】本题主要考查了三角形内角和定理，三角形外角的像这种，角平分线的定义，垂直的定义，熟知三角形内角和为180度是解题的关键．

◎模型七 两外角角平分线模型

【条件】△ABC中，BI、CI分别是△ABC的外角的角平分线，且相交于点O.
【结论】.
【证明】∵BO是∠EBC平分线，∴，∵CO是∠FCB平分线，∴
由△BCO中内角和定理可知：∠O=180°-∠2 -∠5 =180°--=180°--===.
31．（2022·江苏·江阴市祝塘第二中学七年级阶段练习）如图，在△ABC中，设∠A＝x°，∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2；…；∠A2021BC与∠A2021CD的平分线相交于点A2022，得∠A2022，则∠A2022是（　　）度．

A．x B．x C．x D．x
【答案】C
【分析】先由三角形的外角性质得∠A＝∠ACD−∠ABC，∠A1＝∠A1CD−∠A1BC，再由角平分线的定义得到∠A1BC＝∠ABC，∠A1CD＝∠ACD，从而可以得到∠A1＝∠ACD− ∠ABC＝∠A，同样的道理可得，∠A2＝∠A1，∠A3＝∠A2，…，最后得到∠A2022的度数．
【详解】解：∵∠ACD是△ABC三角形的外角，∠A1CD是△A1BC的外角，
∴∠A＝∠ACD−∠ABC，∠A1＝∠A1CD−∠A1BC，
∵BA1和CA1分别是∠ABC和∠ACD的角平分线，
∴∠A1BC＝∠ABC，∠A1CD＝∠ACD，
∴∠A1＝∠ACD−∠ABC＝∠A＝x°，
同理可得，∠A2＝∠A1＝×x°，∠A3＝∠A2＝××x°，…，
∴∠A2022＝x°，
故选：C．
【点睛】本题考查了三角形的外角性质、角平分线的定义，解题的关键是熟练应用三角形外角的性质定理．
32．（2022·浙江·八年级专题练习）如图，中，，BD平分，平分的外角，、交于点，则的度数（　　）

A． B． C． D．
【答案】A
【分析】设，根据外角性质得出，再由角平分线的性质得出，，最后根据外角性质得出，将，的值代入式子中进而得出结果．
【详解】解：设，
根据外角性质可知：，
平分，平分的外角，
，．
根据外角性质：，
．
故选：A．
【点睛】本题考查角平分线、外角的性质的理解与运用能力．主要涉及以下知识点：三角形的一个外角等于与它不相邻的两个内角和；角平分线分得的两个角相等，都等于该角的一半．灵活运用相关知识点是解本题的关键．
33．（2022·陕西·西安博爱国际学校八年级期末）如图，在△ABC中，∠ABC=75°，∠A=40°，∠ACD是△ABC的外角，若∠ABC与∠ACD的平分线交于点P，则∠BPC的大小为_____．

【答案】20°##20度
【分析】由三角形的外角性质可得∠ACD=115°，再由角平分线的定义可得∠PBC=32.5°，∠PCD=57.5°，再利用三角形的外角性质即可求∠BPC的度数．
【详解】解：∵∠ABC=75°，∠A=40°，∠ACD是△ABC的外角，
∴∠ACD=∠ABD+∠A=115°，
∵∠ABC与∠ACD的平分线交于点P，
∴∠PBC=∠ABC=37.5°，∠PCD=∠ACD=57.5°，
∵∠PCD是△BCP的外角，
∴∠BPC=∠PCD-∠PBC=20°．
故答案为：20°．
【点睛】本题主要考查三角形的外角性质，解答的关键是熟记三角形的外角性质并灵活运用．
34．（2022·陕西·西安市曲江第一中学八年级期末）如图，在中，的内角和外角的角平分线交于点P，已知，则的度数为____________．

【答案】##84度
【分析】根据AP为∠CAB的角平分线， BP为外角∠CBD的平分线，可知∠CAM=∠BAP=∠BAC，∠PBC=∠PBD=∠CBD，另外根据∠CBD=∠C+∠CAB，∠PBD=∠PAB+∠P可得∠P=∠C，从而可以求出答案．
【详解】解：如下图，

AP为∠CAB的角平分线，BP为外角∠CBD的平分线，两角平分线交于点P， ∠CAM=∠BAP=∠BAC，∠PBC=∠PBD=∠CBD，
∠CBD=∠C+∠CAB，
∠PBC=∠PBD=(∠C+2∠PAB) =∠C+∠PAB，
∠PBD=∠PAB+∠P，
∠P=∠C，
，
，
【点睛】本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键。
35．（2022·江苏镇江·七年级期中）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．

(1)如果∠ABC＝50°，∠ACB＝60°，则∠BPC= °；
(2)如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，直接写出∠Q与∠BPC之间满足的数量关系 ；
(3)如图③，延长线段BP、QC交于点E，若∠Q=∠E，求∠A的度数．
【答案】(1)125
(2)∠Q+∠BPC=180°
(3)∠A＝72°
【分析】（1）依据∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4的度数，依据三角形内角和定理，即可得到∠BPC的度数；
（2）根据角平分线的定义和平角的定义可得出，再由四边形的内角和定理可得结论；
（3）根据题意求出∠Q=54°，从而得∠QBC+∠QCB=126°，∠MBC+∠NCB=252°，∠ABC+∠ACB=108°，最后由三角形内角和定理可得结论．
（1）
如图，
∵∠ABC=50°，∠ACB=60°，∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4=25°+30°=55°，
∴△BCP中，∠P=180°-55°=125°，
故答案为：125；

（2）
∵BP平分∠ABC，
∴
∵BQ平分
∴
又
∴，
同理可得，
∵
∴
（3）
∵∠EBQ＝90°．且∠Q＝∠E，
∴∠E+∠E=90°,
∴∠E=36°，,
∴∠Q=54°
∴∠QBC+∠QCB=126°，
∴∠MBC+∠NCB=252°
∴∠ABC+∠ACB=108°，
∴∠A＝180°-（∠ABC+∠ACB）=72°．
【点睛】本题是三角形综合题，考查了三角形内角和定理、外角的性质，角平分线定义等知识；灵活运用三角形的内角和定理、外角的性质是解题的关键．
◎模型八 内外角角平分线模型

【条件】△ABC中，BP、CP分别是△ABC的内角和外角的角平分线，且相交于点P.
【结论】
【证明】 ∵BP是∠ABC平分线，∴ ∵CP是∠ACE平分线，∴
由△ABC外角定理可知：∠ACE=∠ABC+∠A即：2∠1=2∠3+∠A ……①
对①式两边同时除以2，得：∠1=∠3+ ……②又在△BPC中由外角定理可知：∠1=∠3+∠P ……③
比较②③式子可知：.==.

36．（2022·江苏·江阴市周庄中学七年级阶段练习）如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①；②∠ACB=2∠ADB；③∠ADC=90°﹣∠ABD；④∠BDC=∠BAC．其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
【答案】C
【分析】利用AD平分∠EAC，推出∠EAD=∠CAD，结合等腰三角形的性质及三角形的外角性质判断①正确；根据，得到∠ADB=∠DBC，再由BD平分∠ABC，得到∠ABC=2∠DBC，由此判断②正确；根据两直线平行，内错角相等可得∠ADC=∠DCF，再根据三角形的一个外角等于与它不相邻的两个内角的和，角平分线的定义整理可得∠ADC=90°﹣∠ABD，判断出③正确；根据∠ACF＝2∠DCF，∠ACF＝∠BAC＋∠ABC，∠ABC＝2∠DBC，∠DCF＝∠DBC＋∠BDC，得出∠BAC＝2∠BDC，判断出④错误．
【详解】解：∵AD平分∠EAC，
∴∠EAD=∠CAD，
∵∠EAC=∠ABC+∠ACB，∠ABC＝∠ACB，
∴∠EAD=∠CAD=∠ABC=∠ACB，
∴，故①正确；
∵，
∴∠ADB=∠DBC，
∵BD平分∠ABC，
∴∠ABC=2∠DBC，
∴∠ACB＝2∠ADB，故②正确；
∵，
∴∠ADC=∠DCF，
∵CD是∠ACF的平分线，
∴∠ADC=∠ACF
=（∠ABC+∠BAC）
=（180°﹣∠ACB）
=（180°﹣∠ABC）
=90°﹣∠ABD
故③正确；
∵∠ACF＝2∠DCF，∠ACF＝∠BAC＋∠ABC，∠ABC＝2∠DBC，∠DCF＝∠DBC＋∠BDC，
∴∠BAC＝2∠BDC，故④错误；
综上分析可知，正确的结论有3个，故C正确．
故选：C．
【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，三角形的内角和定理，平行线的判定与性质，熟记各性质并综合分析，理清图中各角度之间的关系，是解题的关键．
37．（2022·四川宜宾·七年级期末）如图，BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，若∠A＝45°，∠P＝40°，则∠C的度数为（     ）

A．30° B．35° C．40° D．45°
【答案】B
【分析】根据三角形内角和定理，得∠A+∠ADG=∠C+∠GBC，∠A+∠ADE=∠P+∠PBE．根据角平分线的定义，得到∠GBC=2∠PBE，∠ADG=2∠ADE，进而推断出∠A+∠C=2∠P，从而解决此题．
【详解】解：∵∠A+∠ADG+∠AGD=180°，∠ABC+∠C+∠BGC=180°，
∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC，
又∵∠AGD=∠BGC，
∴∠A+∠ADG=∠C+∠GBC．
∴∠A-∠C=∠GBC-∠ADG．
同理，∠A+∠ADE=∠P+∠PBE．
∴∠A-∠P=∠PBE-∠ADE．
∵BP平分∠ABC，DP平分∠ADC，
∴∠GBC=2∠PBE，∠ADG=2∠ADE．
∴∠A-∠C=2（∠A-∠P）．
∴∠A+∠C=2∠P．
又∵∠A=45°，∠P=40°，
∴∠C=35°．
故选：B．
【点睛】本题主要考查三角形内角和定理以及角平分线的性质，熟练掌握三角形内角和定理以及角平分线的性质是解决本题的关键．
38．（2021·江苏·南通市通州区育才中学七年级阶段练习）如图，在中，，的平分线交于点，是外角与内角平分线交点，是，外角平分线交点，若，则_____________度．

【答案】30
【分析】根据角平分线的性质和平角定义可得∠OCD＝∠ACO＋∠ACD＝90°，根据外角的性质可得，继而即可求解．
【详解】解：∵平分，平分的外角
∴，
∵
∴
∴
∴

【点睛】本题考查角平分线的性质，平角定义，三角形的外角性质，解题的关键是根据角平分线的性质和平角定义可得∠OCD＝90°，根据外角的性质求得．
39．（2022·全国·八年级课时练习）在Rt△ABC中，∠BAC＝90°，BD、CE分别平分∠ABC和∠ACB且BD、CE相交于点O，过点O作FO⊥BD交AB于点F，连FD．若∠A﹣∠ACB＝α（0°＜α＜60°），则∠AFD＝_____．

【答案】45°＋α
【分析】延长FO交BC于H，连接DH，证明△FBO≌△HBO（ASA），推出BD垂直平分FH，得到∠AFD=∠DHC，根据四边形内角和推出∠BFO=∠ADO=∠BHO，得到∠CDO=∠CHO，由此证明△OCD≌△OCH，得到CD=CH，利用三角形内角和求出∠CHD，即可得到∠AFD的度数．
【详解】解：如图，延长FO交BC于H，连接DH，

∵∠BAC−∠ACB＝α，
∴∠ACB＝90°−α，
∵FO⊥BD，
∴∠BOF=∠BOH＝90°，
∵BD平分∠ABC，
∴∠FBO=∠HBO，
∵OB=OB，
∴△FBO≌△HBO（ASA），
∴∠BFO=∠BHO，OF=OH，
∴BD垂直平分FH，
∴DF=DH，
∴∠DFH=∠DHF，
∴∠AFD=∠DHC，
∵∠BAC＝90°，∠FOD＝90°，
∴∠AFO+∠ADO＝180°，
∴∠BFO=∠ADO=∠BHO，
∴∠CDO=∠CHO，
∵CO平分∠ACB，
∴∠DCO＝∠HCO，
∵OC=OC，
∴△OCD≌△OCH（AAS），
∴CD=CH，
∴∠CDH=∠CHD=（180°-∠ACB）=45°+α，
∴∠AFD＝∠CHD＝45°＋α，
故答案为：45°＋α．
【点睛】本题是三角形的综合问题，主要考查了直角三角形的性质，三角形的内角和定理、四边形内角和定理、角平分线的定义、全等三角形的判定及性质，解题的关键是熟练掌握全等三角形的判定定理及性质定理．
40．（2022·福建·泉州市城东中学七年级期中）如图1，在△ABC中，∠CBM和∠BCN是△ABC的外角，∠CBM，∠BCN的平分线BD，CD交于点D．

(1)若，求∠BDC的度数：
(2)过点D作DE⊥BD，垂足为D，过点B作BFDE交DC的延长线于点F（如图2），求证：BF是∠ABC的平分线．
【答案】(1)59°
(2)见解析
【分析】(1)依据三角形内角和定理可得，∠ABC+∠ACB＝118°，进而得出∠CBM+∠BCN＝360°﹣118°＝242°，再根据∠CBM，∠BCN的平分线BD，CD交于点D，即可得到，∠DBC+∠BCD＝121°，即可得出∠D＝180°﹣121°＝59°；
(2)依据DE⊥BD，BFDE，即可得出∠2+∠3＝90°，∠1+∠4＝90°，再根据∠3＝∠4，可得∠1＝∠2，进而得到BF是∠ABC的平分线．
（1）
解：∵△ABC中，∠A＝62°，
∴∠ABC+∠ACB＝118°，
又∵∠ABM＝∠ACN＝180°，
∴∠CBM+∠BCN＝360°﹣118°＝242°，
又∵∠CBM，∠BCN的平分线BD，CD交于点D，
∴∠CBD＝∠CBM，∠BCD＝∠BCN，
∴△BCD中，∠DBC+∠BCD＝(∠CBM+∠BCN)＝×242°＝121°，
∴∠BDC＝180°﹣121°＝59°；
（2）
如图2，∵DE⊥BD，BFDE，
∴∠DBF＝180°﹣90°＝90°，
即∠2+∠3＝90°，
∴∠1+∠4＝90°，
又∵∠3＝∠4，
∴∠1＝∠2，
∴BF是∠ABC的平分线．

【点睛】本题考查了三角形的外角性质，平行线的性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．