





所属成套资源:2023-2024学年八年级数学上册精选专题培优讲与练(人教版)
- 培优专题01 与三角形模型有关的角度计算-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 9 次下载
- 培优专题02 与三角形有关的线段和角的问题-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 8 次下载
- 培优专题04 构造三角形全等的方法技巧-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 7 次下载
- 培优专题05 全等三角形十大模型之平移和轴对称模型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 6 次下载
- 培优专题06 全等三角形十大模型之旋转和一线三等角模型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 6 次下载
培优专题03 证明三角形全等的基本思路-2023-2024学年八年级数学上册精选专题培优讲与练(人教版)
展开
这是一份培优专题03 证明三角形全等的基本思路-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题03证明三角形全等的基本思路-原卷版docx、培优专题03证明三角形全等的基本思路-解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
培优专题03 证明三角形全等的基本思路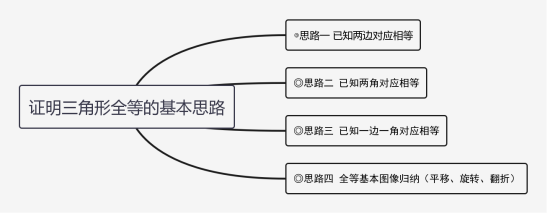 ◎思路一 已知两边对应相等方法归纳:①寻找第三遍对应相等,用“SSS”;②寻找夹角对应相等,用SAS 。1.(2022·全国·八年级专题练习)如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
◎思路一 已知两边对应相等方法归纳:①寻找第三遍对应相等,用“SSS”;②寻找夹角对应相等,用SAS 。1.(2022·全国·八年级专题练习)如图,AB=AC,DB=DC则直接由“SSS”可以判定( ) A.△ABD≌△ACD B.△ABE≌△ACEC.△EBD≌△ECD D.以上答案都不对2.(2022·全国·八年级专题练习)如图,这是一个平分角的仪器,
A.△ABD≌△ACD B.△ABE≌△ACEC.△EBD≌△ECD D.以上答案都不对2.(2022·全国·八年级专题练习)如图,这是一个平分角的仪器,![]() ,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证
,将点A放在一个角的顶点,使AB、AD分别与这个角的两边重合,可证![]() ,从而得到AC就是这个角的平分线.其中证明
,从而得到AC就是这个角的平分线.其中证明![]() 的数学依据是( )
的数学依据是( ) A.SSS B.ASA C.SAS D.AAS3.(2021·江西省宜春实验中学一模)如图所示,在△ABC中,AB=3,AC=2,AD是△ABC的中线,若AD的长为偶数,则AD=___.
A.SSS B.ASA C.SAS D.AAS3.(2021·江西省宜春实验中学一模)如图所示,在△ABC中,AB=3,AC=2,AD是△ABC的中线,若AD的长为偶数,则AD=___.  4.(2022·山东济南·七年级期中)如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为______m.
4.(2022·山东济南·七年级期中)如图,小明想测量池塘两端A,B间的距离,为了安全起见,小明借助全等三角形的知识,用了这样一个间接测量A,B间的距离方法:在地上取一点可以直接到达A点和B点的点C,测得AC长20m,BC长为20m,在AC的延长线上找一点D,使得CD长为20m,在BC的延长线上找一点E,使得CE长为20m,又测得此时D和E的距离为25m,根据小明的数据,可知A,B之间的距离为______m.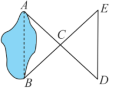 5(2022·全国·八年级专题练习)如图,AC=AE,∠1=∠2,AB=AD.求证:△ABC≌△ADE.
5(2022·全国·八年级专题练习)如图,AC=AE,∠1=∠2,AB=AD.求证:△ABC≌△ADE. ◎思路二 已知两角对应相等方法归纳:①寻找夹边对应相等,用“ASA”;②寻找任一对应角的对边对应相等,用“AAS”6.(2022·浙江·八年级专题练习)用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点A,O,D在同一条直线上,量出CD的长度即知小河AB的宽度.这里判断△AOB≌△DOC的依据是( )
◎思路二 已知两角对应相等方法归纳:①寻找夹边对应相等,用“ASA”;②寻找任一对应角的对边对应相等,用“AAS”6.(2022·浙江·八年级专题练习)用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点A,O,D在同一条直线上,量出CD的长度即知小河AB的宽度.这里判断△AOB≌△DOC的依据是( )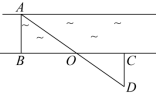 A.SAS或SSA B.SAS或ASA C.AAS或SSS D.ASA或AAS7.(2022·全国·八年级专题练习)如图,
A.SAS或SSA B.SAS或ASA C.AAS或SSS D.ASA或AAS7.(2022·全国·八年级专题练习)如图,![]() ,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,则BE=( )
,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,则BE=( )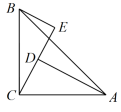 A.1cm B.0.8cm C.4.2cm D.1.5cm8.(2022·上海·七年级专题练习)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带________去玻璃店.
A.1cm B.0.8cm C.4.2cm D.1.5cm8.(2022·上海·七年级专题练习)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带________去玻璃店.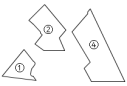 9.(2022·江苏·八年级专题练习)如图,在
9.(2022·江苏·八年级专题练习)如图,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 于点E,若
于点E,若![]() 的面积为
的面积为![]() ,则阴影部分的面积为________
,则阴影部分的面积为________![]() .
.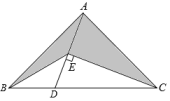 10.(2022·全国·八年级专题练习)如图,已知∠D=∠B,DF⊥AC,BE⊥AC.
10.(2022·全国·八年级专题练习)如图,已知∠D=∠B,DF⊥AC,BE⊥AC. (1)求证:AD∥BC;(2)若AE=CF,求证:△AFD≌△CEB. ◎思路三 已知一边一角对应相等方法归纳:①有一边和该边的对角对应相等,寻找另一角对应相等,用“AAS”;②有一边和该边的邻角对应相等,寻找该角的另一边对应相等,用“SAS”;③有一边和该边的邻角对应相等,寻找另一角对应相等,用“AAS”或“ASA”。11.(2022·全国·八年级课时练习)如图,AB
(1)求证:AD∥BC;(2)若AE=CF,求证:△AFD≌△CEB. ◎思路三 已知一边一角对应相等方法归纳:①有一边和该边的对角对应相等,寻找另一角对应相等,用“AAS”;②有一边和该边的邻角对应相等,寻找该角的另一边对应相等,用“SAS”;③有一边和该边的邻角对应相等,寻找另一角对应相等,用“AAS”或“ASA”。11.(2022·全国·八年级课时练习)如图,AB![]() DE,AB=DE,下列条件中,不能判定△ABC≌△DEF的是( )
DE,AB=DE,下列条件中,不能判定△ABC≌△DEF的是( )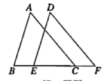 A.DF
A.DF![]() AC B.∠A=∠D C.CF=BE D.AC=DF12.(2022·全国·八年级专题练习)如图,点B,C,E在同一直线上,且
AC B.∠A=∠D C.CF=BE D.AC=DF12.(2022·全国·八年级专题练习)如图,点B,C,E在同一直线上,且![]() ,
,![]() ,
,![]() ,下列结论不一定成立的是( )
,下列结论不一定成立的是( )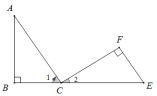 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 13.(2021·湖北·襄阳市樊城区青泥湾中学八年级阶段练习)如图,点D,E分别在线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是______(只需一个即可,图中不能再添加其他点或线)
13.(2021·湖北·襄阳市樊城区青泥湾中学八年级阶段练习)如图,点D,E分别在线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是______(只需一个即可,图中不能再添加其他点或线)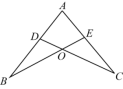 14.(2020·江苏·南京市金陵汇文学校八年级开学考试)如图,已知∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.(1)若以“ASA”为依据,还需要添加一个条件为___________;(2)若以“AAS”为依据,还需要添加一个条件为___________.
14.(2020·江苏·南京市金陵汇文学校八年级开学考试)如图,已知∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.(1)若以“ASA”为依据,还需要添加一个条件为___________;(2)若以“AAS”为依据,还需要添加一个条件为___________.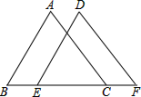 15.(2022·全国·八年级专题练习)已知:如图,点E、F在CD上,且∠A=∠B,AC
15.(2022·全国·八年级专题练习)已知:如图,点E、F在CD上,且∠A=∠B,AC![]() BD,CF=DE.求证:ΔAEC≌ΔBFD.
BD,CF=DE.求证:ΔAEC≌ΔBFD.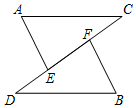 ◎思路四 全等基本图像归纳(平移、旋转、翻折)16.(2022·山东烟台·八年级期末)如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE ⊥DE ,则△BDC通过下列变换能与△ACE重合的是( )
◎思路四 全等基本图像归纳(平移、旋转、翻折)16.(2022·山东烟台·八年级期末)如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE ⊥DE ,则△BDC通过下列变换能与△ACE重合的是( )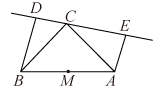 A.绕点C逆时针旋转90度 B.沿AB的垂直平分线翻折C.绕AB的中点M顺时针旋转90度 D.沿DE方向平移17.(2020·山东济宁·八年级期末)如图,在等边
A.绕点C逆时针旋转90度 B.沿AB的垂直平分线翻折C.绕AB的中点M顺时针旋转90度 D.沿DE方向平移17.(2020·山东济宁·八年级期末)如图,在等边![]() 中,
中,![]() ,将线段
,将线段![]() 沿
沿![]() 翻折,得到线段
翻折,得到线段![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() 以下说法:①
以下说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )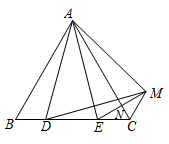 A.
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个18.(2019·安徽合肥·八年级期末)如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=
个18.(2019·安徽合肥·八年级期末)如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=![]() EC中,正确的是_____.
EC中,正确的是_____. 19.(2022·黑龙江哈尔滨·二模)如图,在矩形
19.(2022·黑龙江哈尔滨·二模)如图,在矩形![]() 中,
中,![]() ,点E是边
,点E是边![]() 上一点,连接
上一点,连接![]() ,过点E作
,过点E作![]() ,交
,交![]() 于点F,将
于点F,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,若
,若![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.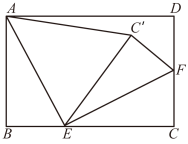 20.(2021·山东临沂·八年级期末)如图,点
20.(2021·山东临沂·八年级期末)如图,点![]() 为定角
为定角![]() 的平分线上的一个定点,
的平分线上的一个定点,![]() ,
,![]() ,且
,且![]() 与
与![]() 互补,若
互补,若![]() 在绕点
在绕点![]() 旋转的过程中,其两边分别与
旋转的过程中,其两边分别与![]() ,
,![]() 相交于
相交于![]() ,
,![]() 两点.
两点.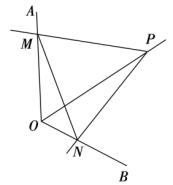 (1)试判断
(1)试判断![]() 的形状,并给出证明;(2)
的形状,并给出证明;(2)![]() 的值是否为定值?若是请求出这个定值,若不是,请说明理由;(3)四边形
的值是否为定值?若是请求出这个定值,若不是,请说明理由;(3)四边形![]() 的面积是否为定值?请说明理由.
的面积是否为定值?请说明理由.
相关试卷
这是一份培优专题16 分式的运算-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题16分式的运算-原卷版docx、培优专题16分式的运算-解析版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
这是一份培优专题12 最短路径-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题12最短路径-原卷版docx、培优专题12最短路径-解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份培优专题09 全等三角形十大模型之角平分线和半角模型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题09全等三角形十大模型之角平分线和半角模型-原卷版docx、培优专题09全等三角形十大模型之角平分线和半角模型-解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。









