培优专题05 全等三角形十大模型之平移和轴对称模型-2023-2024学年八年级数学上册精选专题培优讲与练（人教版）

这是一份培优专题05 全等三角形十大模型之平移和轴对称模型-2023-2024学年八年级数学上册精选专题培优讲与练（人教版），文件包含培优专题05全等三角形十大模型之平移和轴对称模型-原卷版docx、培优专题05全等三角形十大模型之平移和轴对称模型-解析版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
培优专题05 全等三角形的十大模型之平移、轴对称模型（题型较难，根据情况选做，部分题目是后面学习内容）◎模型一：平移模型【模型解读】把△ABC沿着某一条直线l平行移动，所得到△DEF与△ABC称为平移型全等三角形，图①，图②是常见的平移型全等三角线.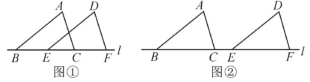【常见模型】 1．（2022·江西赣州·八年级期末）我们知道两个全等的直角三角形（△ABD和△ACE）可以拼成一个等腰三角形（如图1），那么对其中一个直角三角形作适当改变又能得到什么结论呢？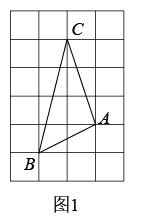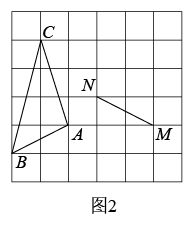现在我们一起来探究吧．(1)如图2，将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC，求证：MB＝MC．(2)将CE向上平移，连接DE，M是DE的中点，连接MB、MC．①如图3，当∠CAE=∠BAD时，求证：MB＝MC；②当∠CAE＞∠BAD时，在图4中补全相应的图形，并直接写出MB、MC的数量关系_______． 2．（2022·湖北荆州·八年级期末）如图，所有的网格都是由边长为1的小正方形构成，每个小正方形的顶点称为格点，△ABC为格点三角形．(1)如图1，计算图中格点△ABC的面积为_______；(2)如图，图2、图3、图4都是6×6的正方形网格，点M、点N都是格点①在图2中作格点△MNP，使△MNP，与△ABC全等；②在图3中作格点△MDE，使△MDE由△ABC平移而得；③在图4中作格点△NFG，使△NFG与△ABC关于某条直线对称．  3．（2022·山西·大同市云州区初级示范中学校二模）数学活动—三角形平移中的数学问题．问题情境：数学活动课上，老师出示了一个问题：如图1，将两块全等的直角三角形纸片和的斜边放在同一直线上，其中，顶点C与顶点E重合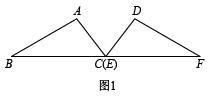．(1)独立思考：将向左平移使得AC的中点G恰好落在DE上，连接AE，CD，AD，如图2，试判断四边形AECD的形状并证明．(2)合作交流：①“希望”小组受此问题的启发，将沿CB方向平移，使得DE与AB交于点M，DF交AC于点N，DF交AB于点H，如图3，求证：．②“希望”小组还发现图3中还有其它相等的线段，在不添加字母的前提下，请你再写出一组相等的线段．(3)提出问题：老师要求各小组向“希望”小组学习，在图3的基础上继续探索．“爱心”小组提出的问题是：如图3，若M恰好是DE的中点，请直接写出线段HM的长度，请解答“爱心”小组提出的问题．  4．（2021·江苏扬州·八年级期末）如图，Rt△ABC与Rt△DEF的边BC、EF在直线l上，∠ACB＝∠EDF＝90°，DE＝DF＝，Rt△DEF沿直线l向左平移．（1）如图1，当点F与点B重合时，连接AE，若AC＝，BC＝3，判断△ABE的形状，并说明理由；（2）如图2，当点D刚好落在AB的中点处，若AB＝4，求CE长；（3）如图3，当点E与点C重合时，若点D刚好落在边AB上，过点F作FM⊥BC，交AB于点M，若AC＝，求FM长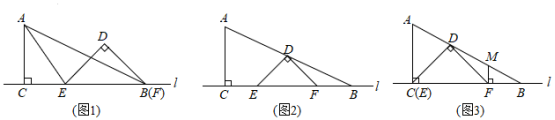．◎模型二：轴对称模型【模型解读】将原图形沿着某一条直线折叠后，直线两边的部分能够完全重合，这两个三角形称之为轴对称型全等三角形，此类图形中要注意期隐含条件，即公共边或公共角相等.【常见模型】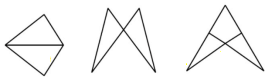   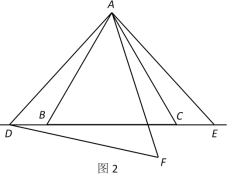5．（2019·山东威海·七年级期末）已知，△ABC为等边三角形，点D，E为直线BC上两动点，且BD＝CE． 点F，点E关于直线AC成轴对称，连接AE，顺次连接A，D，F．（1）如图1，若点D，点E在边BC上，试判断△ADF的形状并说明理由；（2）如图2，若点D，点E在边BC外，求证：．  6．（2022·河南南阳·八年级期末）【教材呈现】东师版数学八年级上册教材页的部分内容，我们都知道演绎推理的方法是研究图形属性的重要方法，请你写出完整的证明过程．我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图，直线是线段的垂直平分线，是上任一点，连接、，将线段沿直线对称，我们发现与完全重合，由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．请你结合图形把已知和求证补充完整，并写出证明过程．已知：如图，，垂足为点，______，点是直线上的任意一点．求证：______．证明：【学以致用】如图，是线段的垂直平分线，则与有何关系？请说明理由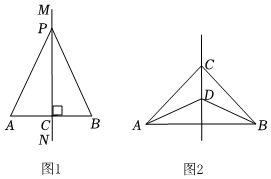． 7．（2022·山西·八年级期末）综合与实践问题情境：如图（1），在Rt△ABC中，AB＝AC，∠BAC＝90°，D为△ABC外的一点，且BD＝BC，∠DBC＝30°，连接AD．(1)若BC＝4，则D到BC边的距离为______．(2)小明在图（1）的基础上，以AB为对称轴构造△ABD的轴对称图形△ABE，得到图（2），连接CE，请判断△BCE的形状，并证明你的结论．(3)在图（2）中，试猜想AE与AD的数量和位置关系，并证明你的猜想．  8．（2022·河南南阳·八年级期末）教材呈现：如图是华师版八年级上册数学教材第94页的部分内容．线段垂直平分线我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴．如图，直线MN是线段AB的垂直平分线，P是MN上任一点，连结PA、PB．将线段AB沿直线MN对折，我们发现PA与PB完全重合．由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．已知：如图，MN⊥AB，垂足为点C，AC＝BC，点P是直线MN上的任意一点求证：PA＝PB．分析：图中有两个直角三角形APC和BPC，只要证明这两个三角形全等，便可证得PA＝PB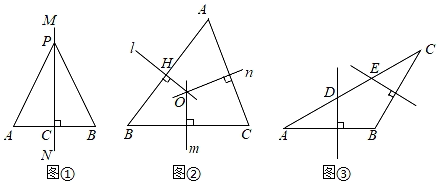．（1）请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程；（2）如图②，在△ABC中，直线l，m，n分别是边AB，BC，AC的垂直平分线．求证：直线l、m、n交于一点；（请将下面的证明过程补充完整）证明：设直线l，m相交于点O．（3）如图③，在△ABC中，AB＝BC，边AB的垂直平分线交AC于点D，边BC的垂直平分线交AC于点E，若∠ABC＝120°，AC＝15，则DE的长为　   　．