




- 培优专题09 全等三角形十大模型之角平分线和半角模型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 5 次下载
- 培优专题10 等腰三角形的性质与判定-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 5 次下载
- 培优专题12 最短路径-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 7 次下载
- 培优专题13 四招轻松搞定幂的问题-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 6 次下载
- 培优专题14 活用乘法公式计算求值-2023-2024学年八年级数学上册精选专题培优讲与练(人教版) 试卷 7 次下载
培优专题11 分类讨论求解等腰三角形的多解问题-2023-2024学年八年级数学上册精选专题培优讲与练(人教版)
展开培优专题11 分类讨论求解等腰三角形的多解问题
◎类型一:对于顶角和底角的分类讨论
方法归纳:方法归纳:对于等腰三角形,只要已知它的一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,就要分两种情况来讨论.在分类时要注意:三角形的内角和等于180°;等腰三角形中至少有两个角相等。
1.(2022·全国·八年级专题练习)若一个等腰三角形有一个内角为82°,则它的底角为( )
A.82° B.16° C.82°或49° D.82°或36°
【答案】C
【分析】分底角为82°与顶角为82°两种情况讨论,当顶角为82°时,底角为![]() ×(180°﹣82°)=49°.
×(180°﹣82°)=49°.
【详解】解:有两种情况:①底角是82°,
②顶角是82°,则底角是![]() ×(180°﹣82°)=49°.
×(180°﹣82°)=49°.
所以底角为82°或49°.
故选:C.
【点睛】本题主要考查了等腰三角形,解决问题的关键是熟练掌握等腰三角形的性质,分类讨论.
2.(2022·江西吉安·八年级期末)某等腰三角形的顶角50°,则其每个底角是( )
A.50° B.60° C.65° D.80°
【答案】C
【分析】根据等腰三角形的性质和三角形的内角和定理即可得到结论.
【详解】解:![]() 等腰三角形的顶角
等腰三角形的顶角![]() ,
,
![]() 每个底角
每个底角![]() ,
,
故选:C.
【点睛】本题考查了等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.
3.(2022·陕西·西安爱知初级中学八年级阶段练习)若等腰三角形有一个内角为40°,则它的顶角度数为________.
【答案】100°或40°
【分析】根据题意可分当顶角为40°时和底角为40°时进行分类求解即可.
【详解】解:①当顶角为40°时,则底角的度数为:![]() ;
;
②当底角的度数为40°时,顶角的度数为![]() ;
;
综上所述:它的顶角的度数为40°或100°;
故答案为:40°或100°.
【点睛】本题主要考查等腰三角形的性质,解题的关键是熟练掌握等腰三角形的性质.
4.(2021·甘肃·庄浪县阳川中学八年级期中)等腰三角形的顶角为36°,它的底角为______.
【答案】72°##72度
【分析】根据等腰三角形的性质和三角形的内角和即可得到结论.
【详解】解:∵(180°-36°)÷2=72°,
∴底角是72°.
故答案为:72°.
【点睛】本题考查了等腰三角形的性质,三角形的内角和定理,熟记各性质定理是解题的关键.
5.(2021·黑龙江·肇源县第二中学九年级期中)以正方形ABCD的边BC为边作等边△PBC,连接AP、DP,则∠APB=_____.
【答案】![]() 或
或![]()
【分析】分两种情况讨论:当点P在正方形ABCD内部时;当点P在正方形ABCD外部时,即可求解.
【详解】解:如图,当点P在正方形ABCD内部时,
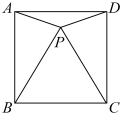
∵△PBC是等边三角形,
∴BP=BC,∠PBC=60°,
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∴BA=BP,∠ABP=∠ABC-∠PBC=90°-60°=30°,
∴![]() ;
;
如图,当点P在正方形ABCD外部时,
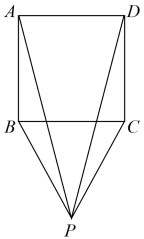
∵△PBC是等边三角形,
∴BP=BC,∠PBC=60°,
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∴BA=BP,∠ABP=∠ABC+∠PBC=90°+60°=150°,
∴![]() ;
;
综上所述,∠APB=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
【点睛】本题主要考查了正方形的性质,等边三角形的性质,等腰三角形的性质,利用分类讨论思想解答是解题的关键.
◎类型二 对腰长和底长的分类讨论
方法归纳:在解答已知等腰三角形边长的问题时,当题目条件中没有明确说明哪条边是“腰”,哪条边是“底”时,往往要进行分类讨论。判定的依据是:三角形的任意两边之和大于第三边;两边之差小于第三边。
6.(2020·全国·八年级单元测试)已知等腰三角形的一边长5cm,另一边长8cm,则它的周长是![]()
![]()
A.18cm B.21cm C.18cm或21cm D.无法确定
【答案】C
【分析】解决本题要注意分为两种情况,5为底或8为底,还要考虑到各种情况是否满足三角形的三边关系来进行解答.
【详解】等腰三角形有两边分别是5cm和8cm,此题有两种情况:①5为底边,那么8就是腰,则等腰三角形的周长为5+8+8=21cm;②8为底边,那么5是腰,则等腰三角形的周长为5+5+8=18cm,∴等腰三角形的周长为21或18cm,故答案为C.
【点睛】本题考查了等腰三角形的性质及基本概念,利用等腰三角形的性质是解决本题的关键.
7.(2021·山东临沂·八年级期中)等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
A.7cm B.7cm或5cm C.5cm D.3cm
【答案】D
【分析】分3cm长的边是腰和底边两种情况,分别利用三角形的周长,等腰三角形的性质和三角形的三边关系进行讨论即可求解.
【详解】解:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是13﹣3﹣3=7cm,而3+3<7,不满足三角形的三边关系.
故底边长是3cm.
故选:D.
【点睛】本题主要考查了等腰三角形的性质和三角形的三边关系,正确理解题意,分两种情况讨论,并且注意到利用三角形的三边关系定理,是解题的关键.
8.(2022·全国·七年级开学考试)一个三角形三个内角的比是3:3:6,且最短边长为10厘米,则该三角形的面积是 _____平方厘米.
【答案】50
【分析】首先根据题意和三角形的内角和确定三角形的形状,然后根据确定的形状求解面积即可.
【详解】解:∵![]() ,三角形的内角和为180°,
,三角形的内角和为180°,
∴![]() ,
,![]() ,
,
该三角形的三个内角分别为45°,45°,90°,
∴该三角形为等腰直角三角形,
∵该三角形最短边长为10厘米,
∴等腰三角形的腰长为10厘米,
∴该三角形面积为:![]() 平方厘米,
平方厘米,
故答案为:50.
【点睛】本题考查三角形的内角和定理,理解并熟记三角形的内角和是解题关键.
9.(2017·山东烟台·七年级期末)已知等腰三角形的周长为![]() ,其中一边长为
,其中一边长为![]() ,那么这个等腰三角形的底边长为____.
,那么这个等腰三角形的底边长为____.
【答案】![]() 或
或![]()
【分析】由于长为5cm的边可能为腰,也可能为底边,故应分两种情况讨论.
【详解】由题意知,应分两种情况:
(1)当腰长为5cm时,则另一腰也为5cm
底边为18−2×5=8cm,
∵0<8<5+5,
∴边长分别为5cm,5cm,8cm,能构成三角形;
(2)当底边长为5cm时,腰的长=(18−5)÷2=6.5cm,
∵0<5<6.5+6.5
∴边长为6.5cm,6.5cm,5cm,能构成三角形.
故答案为5或8.
【点睛】本题考查等腰三角形的性质,分两种情况讨论是解题关键.
10.(2017·新疆·乌鲁木齐市第九十八中学七年级阶段练习)已知等腰三角形一腰上的中线将它的周长分为6和9两部分,则它的底边长是_________.
【答案】7或3
【详解】根据题意画出图形,如图,
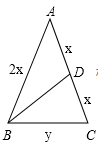
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
有两种情况:
①若AB+AD的长为6,则2x+x=6,
解得x=2,
则x+y=9,即2+y=9,
解得y=7;
②若AB+AD的长为9,则2x+x=9,
解得x=3,
则x+y=6,即3+y=6,
解得y=3;
所以等腰三角形的底边长是7或3.
故答案为7或3.
点睛:本题主要考查等腰三角形的性质、三角形中线的性质和分类讨论思想.利用等腰三角形的性质并运用分类讨论思想是解题的关键所在.
◎类型三:对锐角、直角和钝角三角形的讨论
方法归纳:根据等腰三角形顶角的大小,可以将其分为锐角、直角和钝角三角形,不同的三角形其高、中线、垂直平分线的交点位置均不同,比如锐角三角形腰上的高在这个三角形的内部;直角三角形腰上的高在这个三角形上;纯角三角形腰上的高在这个三角形的外部,因此在解答时需要分类讨论。
11.(2022·山东东营·七年级期末)若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角度数为( )
A.75或15° B.75° C.39° D.30°或80°
【答案】A
【分析】首先根据题意作图,然后分别从等腰三角形一腰上的高在内部与在外部去分析,根据直角三角形中,如果直角边是斜边的一半,则此直角边所对的角是30°角,再由等边对等角的知识,即可求得这个三角形的底角.
【详解】解:如图①:
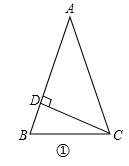
∵CD⊥AB,
∴∠ADC=90°,
∵CD=![]() AC,
AC,
∴∠A=30°,
∵AB=AC,
∴∠B=∠ACB=![]() ;
;
如图②:
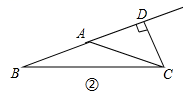
∵CD⊥AB,
∴∠ADC=90°,
∵CD=![]() AC,
AC,
∴∠CAD=30°,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAC=∠B+∠ACB=2∠B=30°,
∴∠B=∠ACB=15°.
∴这个三角形的底角为:75°或15°,故A正确.
故选:A.
【点睛】本题主要考查了直角三角形的性质与等腰三角形的性质,解题的关键是注意数形结合思想与分类讨论思想的应用,小心别漏解.
12.(2022·江苏·八年级课时练习)等腰三角形的一个角是80°,则它底角的度数是( )
A.80°或20° B.80° C.80°或50° D.20°
【答案】C
【分析】根据题意,分已知角是底角与不是底角两种情况讨论,结合三角形内角和等于180°,分析可得答案.
【详解】解:根据题意,一个等腰三角形的一个角等于80°,
①当这个角是底角时,即该等腰三角形的底角的度数是80°,
②设该等腰三角形的底角是x,
则2x+80°=180°,
解可得,x=50°,即该等腰三角形的底角的度数是50°;
综上,该等腰三角形的底角的度数是50°或80°.
故选:C.
【点睛】本题考查了等腰三角形的性质,及三角形内角和定理;通过三角形内角和定理,列出方程求解是正确解答本题的关键.
13.(2021·福建·莆田第七中学八年级期中)在△ABC中,∠A=70°,AB=AC,则∠B的度数是____.
【答案】55°##55度
【分析】根据三角形内角和定理及等腰三角形的两个底角相等解答即可.
【详解】解:
∵在△ABC中,AB=AC,
∴∠C=∠B,
又∵∠A=70°,
∴![]() ,
,
故答案为:55°.
【点睛】本题考查了三角形内角和定理,等腰三角形的性质,掌握等腰三角形两底角相等的性质是解题的关键.
14.(2022·江西吉安·七年级期末)在![]() 中,
中,![]() ,点P是射线BA上的任意一点,当
,点P是射线BA上的任意一点,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的度数为______.
的度数为______.
【答案】108°或72°或36°
【分析】分三种情况讨论:当![]() 时,推出
时,推出![]() ,推出
,推出![]() ;当
;当![]() 时,推出
时,推出![]() ;当
;当![]() 时,推出
时,推出![]() .
.
【详解】解:当![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
综上,∠BPC的度数为108°或72°或36°.
故答案为:108°或72°或36°.
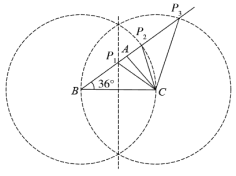
【点睛】本题主要考查了等腰三角形的存在性,解决问题的关键是熟练掌握等边对等角的性质,三角形的三个角都有可能是顶角,分类讨论.
15.(2022·福建泉州·七年级期末)“特征值”的定义:等腰三角形的顶角与其一个底角的度数的比值称为这个等腰三角形的“特征值”,记作“![]() ”.若等腰
”.若等腰![]() 中,
中,![]() ,则它的特征值
,则它的特征值![]() ______.
______.
【答案】![]() 或
或![]()
【分析】分两种情况讨论:若∠A为顶角,若∠A为底角,结合等腰三角形的性质,即可求解.
【详解】解:若∠A为顶角,
则等腰三角形的底角为![]() ,
,
∴特征值![]() ;
;
若∠A为底角,
则等腰三角形的顶角为![]() ,
,
∴特征值![]() ;
;
综上所述,特征值![]()
![]() 或
或![]() .
.
故答案为:![]() 或
或![]()
【点睛】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意到本题中,已知∠A的度数,要分∠A是顶角和底角两种情况,以免造成答案的遗漏.
培优专题11 线段的动点问题-【核心考点突破】2022-2023学年七年级数学上册精选专题培优讲与练(人教版): 这是一份初中人教版本册综合复习练习题,文件包含七年级数学上册培优专题11线段的动点问题-原卷版docx、七年级数学上册培优专题11线段的动点问题-解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
培优专题16 分式的运算-2023-2024学年八年级数学上册精选专题培优讲与练(人教版): 这是一份培优专题16 分式的运算-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题16分式的运算-原卷版docx、培优专题16分式的运算-解析版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
培优专题15 因式分解的类型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版): 这是一份培优专题15 因式分解的类型-2023-2024学年八年级数学上册精选专题培优讲与练(人教版),文件包含培优专题15因式分解的类型-原卷版docx、培优专题15因式分解的类型-解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。












