培优专题16 分式的运算-2023-2024学年八年级数学上册精选专题培优讲与练（人教版）

培优专题16  分式的运算

◎类型一：分式的混合运算

分式的乘法法则:分式乘分式,用分子的积作积的分子,分母的积作积的分母.用式子表示为：.

分式的除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘.用式子表示为：.

分式的乘方法则：分式乘方是把分子、分母各自乘方.用式子表示为：

分式加减法的法则是：同分母分式相加减，分母不变，把分子相加减.用式子表示是：.

异分母分式相加减，先通分，变为同分母的分式，再加减.

用式子表示是：.

1．（2022·河南·郑州市第十九初级中学九年级期末）化简分式：（1﹣）÷的最后的结果是（    ）

A．1﹣x B． C． D．

2．（2022·辽宁沈阳·八年级期末）计算的结果是（    ）

A． B． C． D．x

3．（2021·河北·南皮县桂和中学八年级阶段练习）已知．

（1）化简后的结果为______；

（2）若是整数，且，则的值为______．

4．（2022·福建厦门·八年级期末）化简分式：(1－)÷＝________．

5．（2022·河南南阳·八年级阶段练习）（1）计算：•﹣．

（2）解方程：．

（3）先化简，后求值（+1）÷，其中x＝．

6．（2022·山东·济南市天桥区泺口实验学校八年级期中）化简下列分式．

(1)

(2)÷

(3)÷

7．（2022·吉林·长春博硕学校八年级阶段练习）化简：

(1)；

(2)．

◎类型二：分式的化简求值

8．（2022·河北·石家庄市藁城区第一中学八年级阶段练习）已知，，则的值为（   ）

A． B． C． D．

9．（2022·河南洛阳·八年级期末）已知，则的值为（    ）

A． B． C． D．3

10．（2022·河北保定师范附属学校九年级期末）如果，那么＝_____．

11．（2022·四川成都·八年级期末）已知，则______．

12．（2022·安徽·安庆九一六学校八年级阶段练习）已知x＝+2，y＝﹣2，求代数式的值．

13．（2022·甘肃·陇西县巩昌中学八年级阶段练习）先化简，再求值：，其中，．

14．（2022·四川省彭州中学实验学校八年级期中）先化简，然后从1、﹣1、2、﹣2中选取一个你认为合适的数作为m的值代入求值．

15．（2022·山西·运城市盐湖区教育科技局教学研究室八年级期末）（1）①解不等式组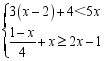，并写出它的非负整数解；

②解方程；

（2）先化简，然后a在、1、2三个数中任选一个合适的数代入求值．

16．（2022·湖北黄石·中考真题）先化简，再求值：，从-3，-1，2中选择合适的a的值代入求值．

17．（2022·四川达州·八年级期末）先化简再求值：，其中，且a是整数．

18．（2022·山东威海·八年级期末）已知，，求下列代数式的值：

(1)

(2)