





所属成套资源:2023-2024学年高二数学上学期精品讲义(人教A版)
专题11 双曲线(课时训练)-2023-2024学年高二数学上学期精品讲义(人教A版)
展开
这是一份专题11 双曲线(课时训练)-2023-2024学年高二数学上学期精品讲义(人教A版),文件包含专题11双曲线课时训练原卷版-高二数学上学期精品讲义人教A版docx、专题11双曲线课时训练解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
专题11 双曲线A组 基础巩固1.(2021·北京房山·)双曲线![]() 的渐近线方程为( )A.
的渐近线方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.(2020·沅陵县第一中学高二月考)等轴双曲线的一个焦点是
2.(2020·沅陵县第一中学高二月考)等轴双曲线的一个焦点是![]() ,则其标准方程为( )A.
,则其标准方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.(2021·全国高二单元测试)以双曲线
3.(2021·全国高二单元测试)以双曲线![]() 的焦点为顶点,顶点为焦点的椭圆方程是( )A.
的焦点为顶点,顶点为焦点的椭圆方程是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.(2021·全国高二课时练习)已知双曲线的下、上焦点分别为
4.(2021·全国高二课时练习)已知双曲线的下、上焦点分别为![]() ,
,![]() ,
,![]() 是双曲线上一点且
是双曲线上一点且![]() ,则双曲线的标准方程为( )A.
,则双曲线的标准方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.(2021·全国高二课时练习)已知双曲线
5.(2021·全国高二课时练习)已知双曲线![]() 的实轴的一个端点为
的实轴的一个端点为![]() ,虚轴的一个端点为
,虚轴的一个端点为![]() ,且
,且![]() ,则双曲线方程为( )A.
,则双曲线方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.(2021·云南玉溪·高三月考(理))双曲线
6.(2021·云南玉溪·高三月考(理))双曲线![]() :
:![]() 的一条渐近线的方程为
的一条渐近线的方程为![]() ,则双曲线
,则双曲线![]() 的离心率为( )A.
的离心率为( )A.![]() B.2 C.4 D.
B.2 C.4 D.![]() 7.(2019·长沙市南雅中学高二月考)已知
7.(2019·长沙市南雅中学高二月考)已知![]() 、
、![]() 为双曲线
为双曲线![]() 的左、右焦点,点
的左、右焦点,点![]() 在
在![]() 上,
上,![]() ,则
,则![]() ( )A.
( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.(2021·全国高二课前预习)已知双曲线的实轴和虚轴等长,且过点(5,3),则双曲线方程为( )A.
8.(2021·全国高二课前预习)已知双曲线的实轴和虚轴等长,且过点(5,3),则双曲线方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.(2021·江西南昌·高三开学考试(理))已知双曲线
9.(2021·江西南昌·高三开学考试(理))已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线l与C的左、右支分别相交于M、N两点,若
的直线l与C的左、右支分别相交于M、N两点,若![]() ,
,![]() ,则双曲线的离心率为( )A.
,则双曲线的离心率为( )A.![]() B.
B.![]() C.2 D.
C.2 D.![]() 10.(2021·全国)已知双曲线C与椭圆
10.(2021·全国)已知双曲线C与椭圆![]() 有共同的焦点,且焦点到该双曲线渐近线的距离等于1,则双曲线C的方程为( )A.
有共同的焦点,且焦点到该双曲线渐近线的距离等于1,则双曲线C的方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.(2020·全国高二单元测试)已知双曲线
11.(2020·全国高二单元测试)已知双曲线![]() 的焦距为
的焦距为![]() ,且双曲线的一条渐近线与直线
,且双曲线的一条渐近线与直线![]() 平行,则双曲线的方程为( )A.
平行,则双曲线的方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.(2021·江苏)在直角坐标系xOy中,F1(-c,0),F2(c,0)分别是双曲线C:
12.(2021·江苏)在直角坐标系xOy中,F1(-c,0),F2(c,0)分别是双曲线C:![]() 的左、右焦点,位于第一象限上的点P(x0,y0)是双曲线C上的一点,△PF1F2的外心M的坐标为
的左、右焦点,位于第一象限上的点P(x0,y0)是双曲线C上的一点,△PF1F2的外心M的坐标为![]() ,△PF1F2的面积为2
,△PF1F2的面积为2![]() a2,则双曲线C的渐近线方程为( )A.y=±x B.y=
a2,则双曲线C的渐近线方程为( )A.y=±x B.y=![]() x C.y=
x C.y=![]() x D.y=±
x D.y=±![]() x13.(2020·全国高二单元测试)设双曲线
x13.(2020·全国高二单元测试)设双曲线![]() 经过点
经过点![]() ,且与
,且与![]() 具有相同渐近线,则
具有相同渐近线,则![]() 的方程为__;渐近线方程为__________.14.(2021·江苏鼓楼·金陵中学)已知焦点在x轴上的双曲线
的方程为__;渐近线方程为__________.14.(2021·江苏鼓楼·金陵中学)已知焦点在x轴上的双曲线![]() 的两条渐近线互相垂直,则
的两条渐近线互相垂直,则![]() ___________.15.(2021·山西平城·大同一中高二月考)已知
___________.15.(2021·山西平城·大同一中高二月考)已知![]() 为双曲线
为双曲线![]() 的左、右焦点过
的左、右焦点过![]() 作
作![]() 的垂线分别交双曲线的左、右两支于B,C两点(如图).若
的垂线分别交双曲线的左、右两支于B,C两点(如图).若![]() ,则双曲线的离心率为___________.
,则双曲线的离心率为___________.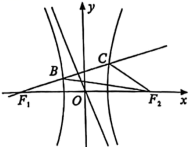 16.(2021·上海浦东新·上外浦东附中高三月考)若双曲线
16.(2021·上海浦东新·上外浦东附中高三月考)若双曲线![]() 的一个焦点为
的一个焦点为![]() ,则实数
,则实数![]() __________.17.(2021·全国高三专题练习(文))(1)求与双曲线
__________.17.(2021·全国高三专题练习(文))(1)求与双曲线![]() 有相同焦点,且经过点
有相同焦点,且经过点![]() 的双曲线的标准方程;(2)已知椭圆
的双曲线的标准方程;(2)已知椭圆![]() 的离心率
的离心率![]() ,求
,求![]() 的值. 18.(2021·全国高三专题练习(理))平面直角坐标系xOy中,求适合下列条件的圆锥曲线的标准方程:(1)求长轴长为4,焦距为2的椭圆的标准方程;(2)求以A(﹣3,0)为一个焦点,实轴长为
的值. 18.(2021·全国高三专题练习(理))平面直角坐标系xOy中,求适合下列条件的圆锥曲线的标准方程:(1)求长轴长为4,焦距为2的椭圆的标准方程;(2)求以A(﹣3,0)为一个焦点,实轴长为![]() 的双曲线的标准方程.
的双曲线的标准方程.
B组 能力提升19.(2021·全国)设![]() 是双曲线
是双曲线![]() 的左焦点.过点
的左焦点.过点![]() 作
作![]() 轴的垂线交双曲线于
轴的垂线交双曲线于![]() 、
、![]() 两点,
两点,![]() 点为双曲线
点为双曲线![]() 的右顶点,若
的右顶点,若![]() 为等边三角形,则双曲线
为等边三角形,则双曲线![]() 的离心率为( )A.
的离心率为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 20.(2021·重庆北碚·西南大学附中高三开学考试)已知双曲线
20.(2021·重庆北碚·西南大学附中高三开学考试)已知双曲线![]() 的左右焦点分别为F1,F2,点M是双曲线右支上一点,满足
的左右焦点分别为F1,F2,点M是双曲线右支上一点,满足![]() ,点N是F1F2线段上一点,满足
,点N是F1F2线段上一点,满足![]() .现将△MF1F2沿MN折成直二面角
.现将△MF1F2沿MN折成直二面角![]() ,若使折叠后点F1,F2距离最小,则
,若使折叠后点F1,F2距离最小,则![]() 为( )A.
为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 21.(2021·浙江)如图,已知椭圆
21.(2021·浙江)如图,已知椭圆![]() 和双曲线
和双曲线![]() 在
在![]() 轴上具有相同的焦点
轴上具有相同的焦点![]() ,
,![]() ,设双曲线
,设双曲线![]() 与椭圆
与椭圆![]() 的上半部分交于A,
的上半部分交于A,![]() 两点,线段
两点,线段![]() 与双曲线
与双曲线![]() 交于点
交于点![]() .若
.若![]() ,则椭圆
,则椭圆![]() 的离心率是( )
的离心率是( )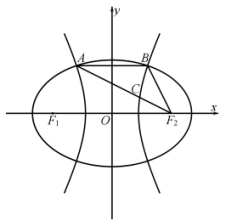 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 22.(2021·永寿县中学高二月考(文))设直线
22.(2021·永寿县中学高二月考(文))设直线![]() 与双曲线
与双曲线![]() 的两条渐近线分别交于
的两条渐近线分别交于![]() 两点.若
两点.若![]() ,其中点M的坐标为
,其中点M的坐标为![]() ,则C的离心率为( )A.
,则C的离心率为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 23.(2021·洛阳市第一高级中学高三月考(文))已知双曲线
23.(2021·洛阳市第一高级中学高三月考(文))已知双曲线![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 向双曲线的一条渐近线引垂线,垂足为
向双曲线的一条渐近线引垂线,垂足为![]() ,交另一条渐近线于
,交另一条渐近线于![]() ,若
,若![]() ,则该双曲线
,则该双曲线![]() 的离心率为______.24.(2021·江苏南京·高二月考)设
的离心率为______.24.(2021·江苏南京·高二月考)设![]() 为双曲线
为双曲线![]() (
(![]() ,
,![]() )的右焦点,过
)的右焦点,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的两条渐近线分别交于A,B两点,且
的两条渐近线分别交于A,B两点,且![]() ,则双曲线
,则双曲线![]() 的离心率为___________.25.(2021·四川省新津中学高二月考(文))有公共焦点
的离心率为___________.25.(2021·四川省新津中学高二月考(文))有公共焦点![]() ,
,![]() 的椭圆和双曲线的离心率分别为
的椭圆和双曲线的离心率分别为![]() ,
,![]() ,点
,点![]() 为两曲线的一个公共点,且满足
为两曲线的一个公共点,且满足![]() ,则
,则![]() 的值为______.26.(2022·江苏高三专题练习)已知双曲线C:
的值为______.26.(2022·江苏高三专题练习)已知双曲线C:![]() (
(![]() ,
,![]() )的渐近线方程为
)的渐近线方程为![]() ,若动点P在C的右支上,
,若动点P在C的右支上,![]() ,
,![]() 分别为C的左,右焦点,
分别为C的左,右焦点,![]() 的最小值是2a(其中O为坐标原点),则
的最小值是2a(其中O为坐标原点),则![]() 的最小值为___________27.(2021·全国高二专题练习)求适合下列条件的双曲线的标准方程:(1)焦点在x轴上,虚轴长为8,离心率为
的最小值为___________27.(2021·全国高二专题练习)求适合下列条件的双曲线的标准方程:(1)焦点在x轴上,虚轴长为8,离心率为![]() ;(2)与双曲线
;(2)与双曲线![]() 有共同的渐近线,且过点
有共同的渐近线,且过点![]() . 28.(2021·江苏高二专题练习)设点
. 28.(2021·江苏高二专题练习)设点![]() 为双曲线
为双曲线![]() 上任意一点,双曲线
上任意一点,双曲线![]() 的离心率为
的离心率为![]() ,右焦点与椭圆
,右焦点与椭圆![]() 的右焦点重合.(1)求双曲线
的右焦点重合.(1)求双曲线![]() 的标准方程;(2)过点
的标准方程;(2)过点![]() 作双曲线两条渐近线的平行线,分别与两渐近线交于点
作双曲线两条渐近线的平行线,分别与两渐近线交于点![]() ,
,![]() ,求证:平行四边形
,求证:平行四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
29.(2021·全国高二课时练习)已知抛物线![]() :
:![]() (
(![]() )的焦点与双曲线
)的焦点与双曲线![]() :
:![]() 右顶点重合.(1)求抛物线
右顶点重合.(1)求抛物线![]() 的标准方程;(2)设过点
的标准方程;(2)设过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,
,![]() 是抛物线
是抛物线![]() 的焦点,且
的焦点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
相关试卷
这是一份专题12 直线与双曲线位置关系(课时训练)-2023-2024学年高二数学上学期精品讲义(人教A版),文件包含专题12直线与双曲线位置关系课时训练原卷版-高二数学上学期精品讲义人教A版docx、专题12直线与双曲线位置关系课时训练解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份专题11 双曲线(重难点突破)-2023-2024学年高二数学上学期精品讲义(人教A版),文件包含专题11双曲线重难点突破原卷版-高二数学上学期精品讲义人教A版docx、专题11双曲线重难点突破解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
这是一份专题09 椭圆(课时训练)-2023-2024学年高二数学上学期精品讲义(人教A版),文件包含专题09椭圆课时训练原卷版-高二数学上学期精品讲义人教A版docx、专题09椭圆课时训练解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。








