专题12 直线与双曲线位置关系（课时训练）-2023-2024学年高二数学上学期精品讲义（人教A版）

专题12 直线与双曲线的位置关系

A组 基础巩固

1．（2021·四川高三月考（理））已知双曲线的下上焦点分别为，，过作双曲线渐近线的垂线，垂足为点，若的面积为，则双曲线的离心率为（    ）

A． B． C． D．

2．（2021·孟津县第一高级中学（文））设为坐标原点，双曲线的右焦点为，点是上在第一象限的点，点满足，且线段互相垂直平分，则的离心率为（    ）

A． B．

C． D．

3．（2021·吉林白山·高三期末（文））已知双曲线：与直线交于，两点，点为上一动点，记直线，的斜率分别为，，的左､右焦点分别为，.若，且的焦点到渐近线的距离为1，则（    ）

A．

B．的离心率为

C．若，则的面积为2

D．若的面积为，则为钝角三角形

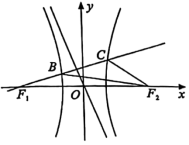
4．（2021·浙江高二单元测试）已知为双曲线的左､右焦点，过作的垂线分别交双曲线的左､右两支于两点(如图).若，则双曲线的渐近线方程为（    ）

A． B．

C． D．

5．（2022·江苏高三专题练习）已知双曲线的右焦点为，右顶点为，，两点在双曲线的右支上，为中点，为轴上一点，且.若，则双曲线的离心率的取值范围是（    ）

A． B． C． D．

6．（2021·四川省内江市第六中学高三月考（理））设为双曲线的右焦点，过点且斜率为的直线与双曲线的两条渐近线分别交于，两点，若，则双曲线的离心率等于（    ）

A． B． C． D．

7．（2021·全国高二课时练习）已知、是双曲线上关于原点对称的两点，是上异于、的动点，设直线、的斜率分别为、．若直线与曲线没有公共点，当双曲线的离心率取得最大值时，且，则的取值范围是（    ）

A． B． C． D．

8．（2021·江西上高二中高二月考（文））已知双曲线，过其右焦点且平行于一条渐近线的直线与另一条渐近线交于点，与双曲线交于点，若，则双曲线的离心率为（    ）

A． B． C． D．

9．（2021·江苏）已知双曲线的左、右焦点分别为、，点在双曲线的右支上，点．若周长的最小值为，则双曲线的渐近线方程为________．

10．（2020·上海）设是双曲线上一点，双曲线的一条渐近线方程为，分别是双曲线的左、右焦点，若，则_______．

11．（2020·全国高二课时练习）过双曲线的右焦点作一条与其渐近线平行的直线，交于点.若点的横坐标为,则的离心率为­       .

12．（2021·全国高三专题练习（文））已知分别为双曲线的左、右焦点，若双曲线左支上存在一点P使得，则双曲线的离心率的取值范围是_________.

13．（2021·全国高二课时练习）双曲线C的离心率为，且与椭圆有公共焦点．

（1）求双曲线C的方程．

（2）双曲线C上是否存在两点A，B关于点（4，1）对称？若存在，求出直线AB的方程；若不存在，说明理由．

14．（2021·全国）已知双曲线的离心率为2，为双曲线的右焦点，为双曲线上的任一点，且点到双曲线的两条渐近线距离的乘积为.

（1）求双曲线的方程；

（2）设过点且与坐标轴不垂直的直线与双曲线相交于点，，线段的垂直平分线与轴交于点，求的值.

B组 能力提升

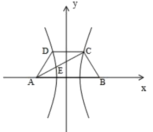
15．（2021·江苏高二专题练习）如图，在梯形中，已知，，双曲线过三点，且以为焦点，则双曲线的离心率为_____________.

16．（2021·江苏高二专题练习）设，分别是双曲线的左､右焦点，若双曲线右支上存在一点，使，为坐标原点，且，则该双曲线的离心率为__________.

17．（2021·江苏高二单元测试）已知双曲线的右焦点为F，左顶点为A，O为坐标原点，以OF为直径作圆交双曲线的一条渐近线于点P，且，则双曲线的离心率________.

18．（2021·上海复旦附中青浦分校高二月考）已知双曲线C：的离心率为，且经过.

（1）求双曲线C的方程；

（2）若过点的直线交双曲线C于x轴下方不同的两点P､Q，设P､Q中点为M，求三角形面积的取值范围.

19．（2020·江苏高二单元测试）如图，若F1，F2是双曲线的两个焦点．

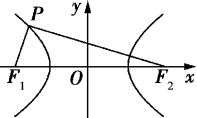
（1）若双曲线上一点M到它的一个焦点的距离等于7，求点M到另一个焦点的距离；

（2）若P是双曲线左支上的点，且，求的面积．

20．（2021·全国高二单元测试）已知椭圆的左、右两个顶点分别为、，曲线是以、两点为顶点，焦距为的双曲线，设点在第一象限且在曲线上，直线与椭圆相交于另一点.

（1）求曲线的方程；

（2）设、两点的横坐标分别为、，求证为一定值；

（3）设△与△（其中为坐标原点）的面积分别为与，且，求的取值范围.

21．（2021·福建高三月考）已知双曲线：(，)的左、右焦点分别为，，双曲线的右顶点在圆：上，且．

(1)求双曲线的标准方程；

(2)动直线与双曲线恰有1个公共点，且与双曲线的两条渐近线分别交于点、，问(为坐标原点)的面积是否为定值？若为定值，求出该定值；若不为定值，试说明理由．

22．（2020·江西省靖安中学高二月考（理））双曲线的一条渐近线方程是，坐标原点到直线的距离为，其中，.

（1）求双曲线的方程；

（2）若是双曲线虚轴在轴正半轴上的端点，过点作直线交双曲线于点，，求时，直线的方程.

.

23．（2021·全国高二课时练习）已知是以，为焦点的双曲线上的一点，且，．

（1）求双曲线的离心率；

（2）过点作直线分别与双曲线两渐近线相交于，两点，若（为坐标原点），，求双曲线的标准方程．

24．（2021·全国高二课时练习）已知双曲线的焦点坐标为，，实轴长为4，

（1）求双曲线的标准方程；

（2）若双曲线上存在一点使得，求的面积．