专题13 抛物线（课时训练）-2023-2024学年高二数学上学期精品讲义（人教A版）

这是一份专题13 抛物线（课时训练）-2023-2024学年高二数学上学期精品讲义（人教A版），文件包含专题13抛物线课时训练原卷版-高二数学上学期精品讲义人教A版docx、专题13抛物线课时训练解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
专题13 抛物线A组 基础巩固1．（2021·四川·成都七中高三期中（文））抛物线上的一点到其焦点的距离等于（    ）A． B． C． D．2．（2021·江西·贵溪市第一中学高二期中（文））已知A（3，2），点F为抛物线的焦点，点P在抛物线上移动，为使取得最小值，则点P的坐标为（    ）A．（0，0） B．（2，2） C． D．3．（2021·江苏如皋·高二月考）已知点M（0，4），点P在曲线上运动，点Q在圆上运动，则的最小值是（    ）A． B． C．4 D．64．（2021·全国·高二课时练习）过点的直线与抛物线交于A，B两点，若线段AB中点的横坐标为2，则（    ）A． B． C． D．5．（2021·重庆南开中学高二期中）由抛物线上一点朝准线作垂线，垂足为，抛物线的焦点为，已知，则（    ）A． B． C． D．6．（2018·浙江诸暨·高二期末）已知抛物线的焦点是，，是抛物线上不与原点重合的两点，且不共线，则(    )A． B．C． D．7．（2021·河南·郸城县第一高级中学一模（文））点为抛物线的焦点，为其准线，过的一条直线与抛物线交于，两点，与交于点．已知点在线段上，若，，按照某种排序可以组成一个等差数列，则的值为（    ）A．或 B．或 C．或 D．或8．（2021·湖南湘潭·一模）已知抛物线：（）的焦点为，点在上，且，若点的坐标为，且，则的方程为（    ）A．或 B．或C．或 D．或9．（2021·黑龙江·大庆实验中学高三月考（文））已知为坐标原点，抛物线上一点到焦点的距离为6，若点为抛物线的准线上的动点，则的最小值为（    ）A．4 B． C． D．10．（2021·全国·高二专题练习）如图，在正方体中，是棱的中点，是侧面上的动点，并且平面，则动点的轨迹是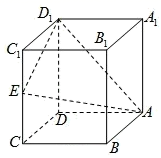（    ）A．圆 B．椭圆 C．抛物线 D．线段11．（2022·全国·高三专题练习）已知抛物线C：的焦点为F，过点F分别作两条直线，，直线l1与抛物线C交于A、B两点，直线l2与抛物线C交于D、E两点，若与的斜率的平方和为1，则的最小值为（　　）A．16 B．20 C．24 D．3212．（2021·全国·高二课时练习）以下关于圆锥曲线的四个命题中是真命题的为______（填序号）.①设A，B为两个定点，k为非零常数，若，则动点P的轨迹是双曲线；②方程的两根可分别作为椭圆和双曲线的离心率；③双曲线与椭圆有相同的焦点；④以过抛物线的焦点的一条弦PQ为直径作圆，则该圆与抛物线的准线相切.13．（2021·河南平顶山·高三月考（理））抛物线的焦点到准线的距离为2，过点的直线与交于，两点，的准线与轴的交点为，若的面积为，则___________.14．（2021·全国·高三专题练习）抛物线的焦点为，已知点为抛物线上的两个动点，且满足，过弦的中点作该抛物线准线的垂线，垂足为，则的最小值为__________ 
B组 能力提升15．（2021·广东中山·模拟预测）为抛物线的焦点，为抛物线内一点，为上的任意一点，的最小值为5，则_______，直线过点，与抛物线交于两点，且为线段的中点，过分别作抛物线的切线，两切线相交于点，则的面积为___________.16．（2021·全国·高二课时练习）已知圆与抛物线相交于，两点，为抛物线的焦点，若直线与抛物线相交于，两点，且与圆相切，切点在劣弧上，当直线的斜率为0时，______；当直线的斜率不确定时，的取值范围是______．17．（2021·全国·高三专题练习（文））探照灯、汽车灯等很多灯具的反光镜是抛物面（其纵断面是拋物线的一部分），正是利用了抛物线的光学性质：由其焦点射出的光线经抛物线反射之后沿对称轴方向射出．根据光路可逆图，在平面直角坐标系中，抛物线，一条光线经过，与轴平行射到抛物线上，经过两次反射后经过射出，则________，光线从点到经过的总路程为________．18．（2021·北京昌平·二模）已知抛物线与椭圆有一个公共焦点，则点的坐标是________；若抛物线的准线与椭圆交于两点，是坐标原点，且是直角三角形，则椭圆的离心率________.19．（2021·全国·高三月考（理））在平面直角坐标系内，已知定点，动点在轴右侧运动（允许动点在轴上），并且点到轴的距离恰好比它到定点的距离小1.（1）求动点的轨迹的方程；（2）斜率存在的直线经过点且与交于，两点，若线段的垂直平分线与轴交于点，求点横坐标的取值范围.
20．（2021·江苏如皋·高二月考）已知抛物线上一点到其焦点F的距离为2.（1）求拋物线方程；（2）直线与拋物线相交于两点，求的长.       21．（2021·全国·高二课时练习）如图，过抛物线的焦点F的直线l交抛物线于点A，B，交其准线于点C，若，且，求此抛物线的方程.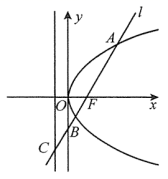
22．（2021·海南昌茂花园学校高三月考）已知动圆过点且与直线相切，圆心的轨迹为曲线．（1）求曲线的方程；（2）若，是曲线上的两个点且直线过的外心，其中为坐标原点，求证：直线过定点．        23．（2021·全国·高二课时练习）动圆与定圆：外切，且与直线：相切，求动圆圆心的轨迹方程．