人教A版（上）第三次月考测试卷（B卷 能力提升）-2023-2024学年高二数学上学期精品讲义（人教A版）

这是一份人教A版（上）第三次月考测试卷（B卷 能力提升）-2023-2024学年高二数学上学期精品讲义（人教A版），文件包含高二上第三次月考测试卷B卷能力提升原卷版-高二数学上学期精品讲义人教A版docx、高二上第三次月考测试卷B卷能力提升解析版-高二数学上学期精品讲义人教A版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
高二（上）第三次月考测试卷（B卷 能力提升）数 学考试时间：120分钟   满分：150分一、单选题：本大题共12小题，每个小题5分，共60分.在每小题给出的选项中，只有一项是符合题目要求的.1．命题“”的否定是（    ）A． B．C． D．2．若双曲线的一条渐近线方程为，则该双曲线的离心率为（    ）A． B． C． D．3．如图是某次文艺比赛中七位评委为其中-位选手所打分数(满分为分)的茎叶图，在去掉一个最高分和一个最低分后所剩个分数的方差为（    ）A． B． C． D．4．为了解某地区的人口年龄分布情况，某机构从该地区年龄在内的居民中随机抽取了位进行调查，并将年龄按，，，，，分组，得到如图所示的频率分布直方图．则下列说法正确的是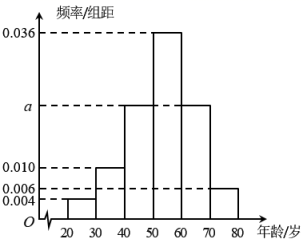（    ）A．频率分布直方图中的值为B．这位居民中有位居民的年龄不低于岁C．估计这位居民的平均年龄为岁D．该地区人口年龄分布在的人数与分布在的人数分别记为，则一定成立5．执行如图所示的程序语句，若输入的值为，输出结果为．则输入的值可能为（    ）A． B． C． D．6．已知，分别为双曲线的左焦点和右焦点，过的直线与双曲线的右支交于，两点，的内切圆半径为，的内切圆半径为，若，则直线的斜率为A．1 B． C．2 D．7．已知直线与曲线的两个不同的交点，则实数的取值范围是（   ）A． B． C． D．8．过抛物线焦点的直线与其交于两点，若，则（    ）A． B． C． D．9．已知椭圆的左、右焦点分别为、，过作轴的平行线交椭圆于两点，为坐标原点，双曲线以为顶点，以直线为渐近线，则双曲线的焦距为（    ）A． B． C． D．10．从，，，，，，这七个数字中随机抽取一个，记事件为“抽取的数字为偶数”，事件为“抽取的数字为的倍数”，则事件发生的概率为（    ）A． B． C． D．11．已知，，实数是常数，，是圆上两个不同点，是圆上的动点，如果，关于直线对称，则面积的最大值是A． B．4 C．6 D．12．已知直线l：x-y+3=0和点A（0，1），抛物线y=x2上一动点P到直线l和点A的距离之和的最小值是（　　）A．2 B． C． D．二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.13．一组数据的极差为_______________________．14．已知命题：若，则；命题，直线与椭圆恒有两个共同点．在命题①；②；③中，所有真命题的序号是_______________________．15．已知圆的圆心为为直线上的动点，过点作圆的切线，切点为，则的最小值为___________．16．如图，，分别是椭圆的左右焦点，以为直径的圆与椭圆交于点，，，，若所在直线垂直平分线段，则椭圆的离心率为______．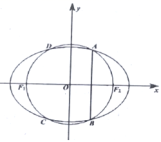
三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤．17．已知命题；命题q：关于x的方程有两个不同的实数根．若为真命题，求实数m的取值范围；若为真命题，为假命题，求实数m的取值范围．     18．为做好传染病的防治工作，某部门收集了所辖个地区一个月中的就诊人数（单位：人）和参与治疗的医务人员人数（单位：人），相关数据如下表： 地地地地地就诊人数（单位：人）参与治疗的医务人员人数（单位：人）（1）研究发现与之间具有线性相关关系，试根据表中统计数据，求出关于的线性回归方程；（2）若该部门将所辖个地区按参与治疗的医务人员人数不超过人和超过人的标准分别划分为“甲类区域”和“乙类区域”．现采用分层抽样的方法在甲乙两类区域参与治疗的所有医务人员中共抽取人进行培训，求所抽取的“甲类区城”的医务人员来自不同地区的概率参考数据：参考公式：，．.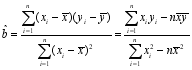
19．为统计某城市居民用水情况．利用随机抽取的位居民某年的月均用水量(单位：)为样本绘制成了如图所示的频率分布直方图．将图中从左至右每个小长方形对应组的中间值为第组左右两个边界值的算术平均数，如与高表示的有序数对作为样本数据，其中记表示取最大值时所对应的的值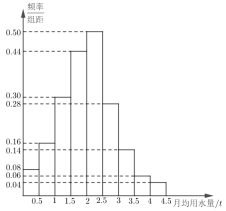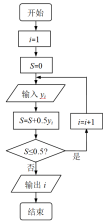．（1）根据频率分布直方图求的值；（2）求程序框图的输出结果的值，令，记．若，则称样本数据符合“左偏分布”；否则不符合“左偏分布”．请问本题的样本数据是否符合“左偏分布”？
20．已知椭圆经过点，且离心率为.（1）求椭圆的方程；（2）不经过点的直线与椭圆交于两点，若点关于原点对称的点为(与点不重合)，直线与轴分别交于两点，求证：点在线段的垂直平分线上.      21．设椭圆的左、右焦点分别为是椭圆上的一点，，原点到直线的距离为.（1）求椭圆的离心率；（2）点为圆上任意点，过点做圆的切线交椭圆于两点.探索关于在时的函数关系式.
22．已知椭圆的右焦点为，点在椭圆上．（1）求椭圆的方程；（2）直线是圆的一条切线，且直线与椭圆相交于点，求面积的最大值．