初中数学北师大版九年级下册1 圆复习ppt课件

这是一份初中数学北师大版九年级下册1 圆复习ppt课件，共28页。PPT课件主要包含了点圆最值---点心线，线圆最值---心垂线，圆中最长弦---直径，过定弦中最小的圆等内容，欢迎下载使用。

平面内一定点P和⊙O上动点E的连线中,当连线过圆心O时,线段PB有最大值和最小值.具体分以下三种情况讨论(规定OP=d,⊙O半径为r)：(i)若P点在⊙O外时,d＞r,如图1:当P,B,O三点共线时,线段PB出现最, PB的最大值为_____，PB的最小值为_____；
(ⅱ)若P点在圆上时,d=r,如图2:当P,B,O三点共线时,线段PB出现最值, PB的最大值为____________________；PB的最小值为________________.
(ⅲ)若P点在⊙O内时,d＜r,如图3:当P,B,O三点共线时,线段PB出现最值, PB的最大值为____, PB的最小值为____.
d+r=2r(即为⊙O的直径)
d-r=0(点D,E重合)
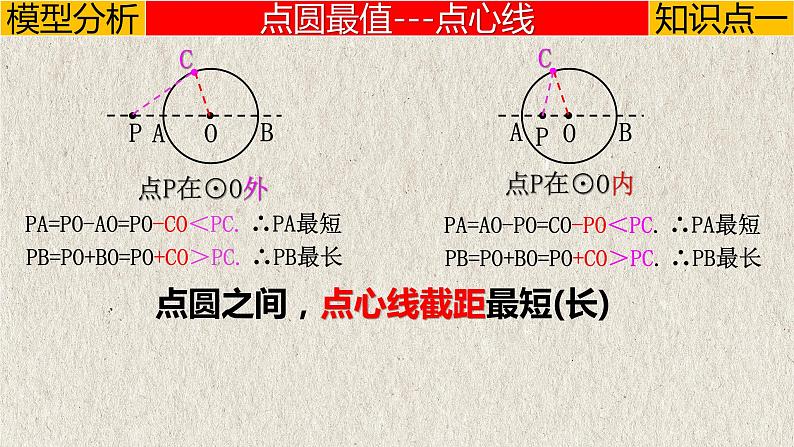
PA=PO-AO=PO-CO＜PC.
PB=PO+BO=PO+CO＞PC.
PA=AO-PO=CO-PO＜PC.
点圆之间，点心线截距最短(长)
【例1】有一架靠在直角墙面的梯子(MN=4)正在下滑,D点出有一只猫紧紧盯住位于梯子MN的正中间E处的老鼠,等待与老鼠距离最小时扑捉.把墙面,梯子,猫和老鼠看成同一平面内的线或点,点D到BA,BC的距离分别为4和2.猫与老鼠的距离DE的最小值为_______.
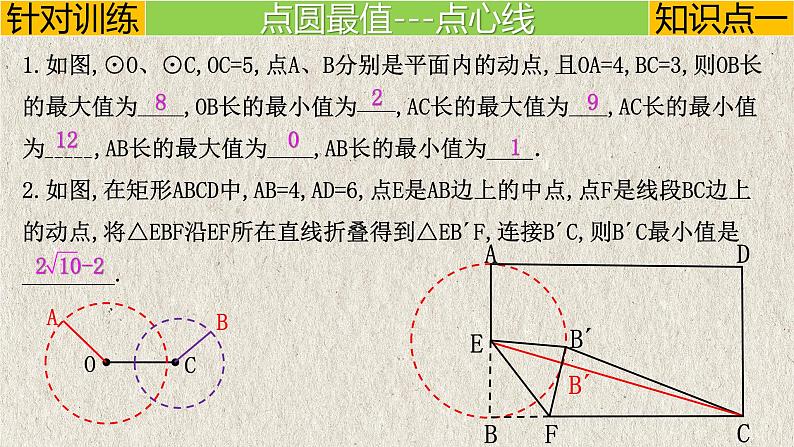
1.如图,⊙O、⊙C,OC=5,点A、B分别是平面内的动点,且OA=4,BC=3,则OB长的最大值为______,OB长的最小值为_____,AC长的最大值为_____,AC长的最小值为_____,AB长的最大值为______,AB长的最小值为____．2.如图,在矩形ABCD中,AB=4,AD=6,点E是AB边上的中点,点F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB´F,连接B´C,则B´C最小值是________.
(i)如图,AB为⊙O的一条定弦,点C为圆上一动点.如图1,若点C在优弧AB上,当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大；如图2,若点C在劣弧AB上,当CH⊥AB且CH的延长线过圆心O时,线段CH即为点C到弦AB的最大距离,此时△ABC的面积最大.
【例2-1】在△ABC中,AB=4,∠C=60º,∠A≥∠B,则BC的长的取值范围是____________,△ABC面积的最大值为____.
(ⅱ)如图,⊙O与直线l相离,点P是⊙O上的一个动点,设圆心O到直线l的距离为d,⊙O的半径为r,则点P到直线l的最小距离是_____,(如图3),点P到直线l的最大距离是_____(如图4).
∵OP+PM＞OM＞OH=OB+BH,OB=OP.
∵AH=OA+OH=OP+OH＞PH＞PM,
①线圆之间,心垂线截距最短(长).
结论：AH最长,BH最短.
【例2】如图,在Rt△ABC中,∠C=90º,AC=6,BC=8,点F在边AC上,并且CF=1,点E为边BC上的动点,△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是_____.
如图,在△ABC中,∠ABC=90º,AB=3,BC=4,O为AC的中点,过点O作OE⊥OF,OE、OF分别交AB、BC于点E、F,则EF的最小值为_______.
1.定圆中最长的弦是直径；
2.定弦中最小的圆是以该弦为直径的圆
3.经过圆中定点最短的弦是垂直于过这点直径的弦；
【例3】在△ABC中,∠ACB=90º,AC=6,BC=8,O为AB的中点,过O作OE⊥OF，OE,OF分别交射线AC,BC于E,F,则EF的最小值为_____.
【简答】∵∠EOF=∠C=90º,
∴C,O均在以EF为直径的圆上.
∵EF是圆的直径,O、C均在圆上,且OC长度固定,要使EF最短,则圆最小,要使圆最小,由于OC为固定长度,则OC为直径时,圆最小,此时EF=CO=OA=OB=5(斜边上中线等于斜边一半)
过⊙O内一点P的最短的弦是与OP垂直的弦AB,
连接OB,OC,过点O作OH⊥CD于点H.
∴PB2=OB2-OP2,CH2=OC2-OH2.
∵OB=OC,OP＞OH.
∴过点P的最短的弦是与OP垂直的弦AB,
1.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心,1为半径作⊙D,P为⊙D上的一个动点,连接AP,OP,AO,则△AOP面积的最大值为_______.2.如图,在边长为2的菱形ABCD中,∠A=60º,M是AD边的中点,N是AB上一个动点,将△AMN沿MN所在直线翻折得到△A´MN,连接A´C,则A´C长的最小值为______.
3.如图,在矩形ABCD中,AB=60,AD=45,P,Q分别是AB,AD边上的动点,PQ=52,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为_____.
∴当OH最短时，MN最长.
4.如图,在Rt△ABC中,∠C=90º,BC=6,AC=8,D,E分别是BC,AC上的一点,且DE=6.若以DE为直径的圆与斜边AB相交于M,N两点,则MN的最大值为_____. 5.如图,在⊙O中,直径AB=12,点D是圆上任意一点(A,B除外),P为CD的中点,过点D作DE⊥AB于点E,连接AD,EP.则EP的最大值为____.
6.如图,AB是⊙O的弦,点C是ACB上的动点(C不与A,B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是_____. 7.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90º,M为OA的中点,OA=5,OB=12.将△COD绕点O旋转,连接AD,CB,并延长交于点P,连接MP,则MP的最大值为_____.
9.在⊙O中,直径AB=6,BC是弦,∠ABC=30º,点P在BC上,点Q在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度；(2)如图2,当点P在BC上移动时,求PQ长的最大值．
10.如图,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC, (1)求∠DPE的度数；(2)求DE的最小值.
【简答】∵∠PEC=∠PDC=90º,故四边形PDCE对角互补,故PDCE四点共圆,如图.∠EOD=2∠ECD=120º,要使得DE最小,则要使圆的半径最小,故直径PC最小,当CP⊥AB时,PC最短为 ,则可求出DE=4.5.