几何模型5.5 “母子、旋转、三平行”模型（相似模型）-中考数学二轮复习必会几何模型剖析（全国通用）课件PPT

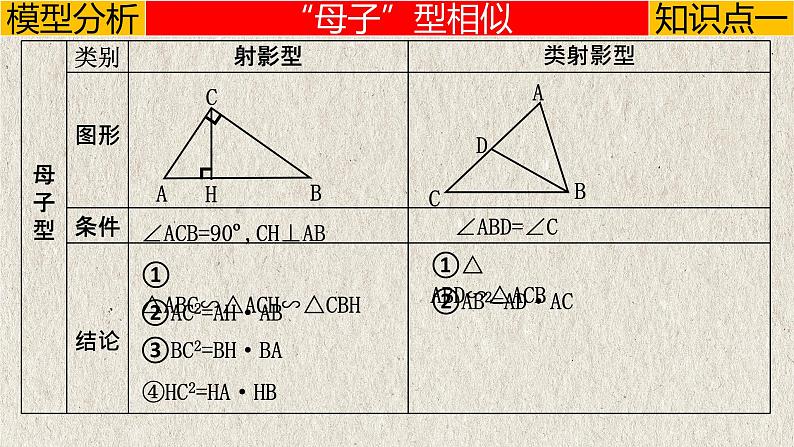
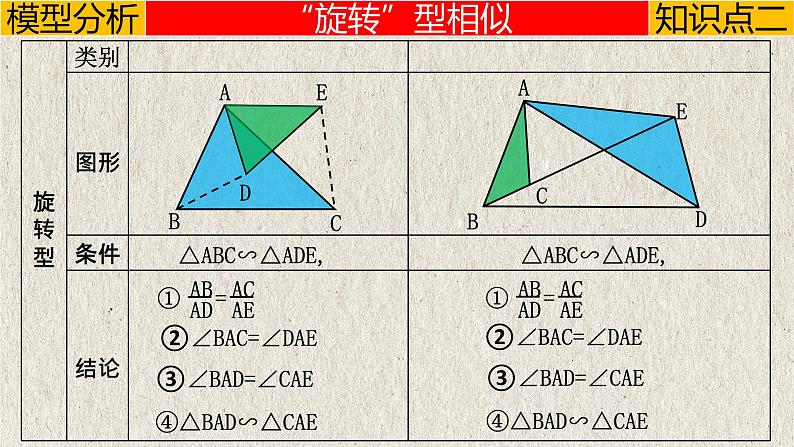
这是一份几何模型5.5 “母子、旋转、三平行”模型（相似模型）-中考数学二轮复习必会几何模型剖析（全国通用）课件PPT，共22页。PPT课件主要包含了“母子”型相似，“旋转”型相似，三平行模型，④HC2HA·HB，②AC2AH·AB，∠ABD∠C，②AB2AD·AC，④△BAD∽△CAE，△ABC∽△ADE，②∠BAC∠DAE等内容，欢迎下载使用。
∠ACB=90º,CH⊥AB
①△ABC∽△ACH∽△CBH
③BC2=BH·BA
①△ABD∽△ACB
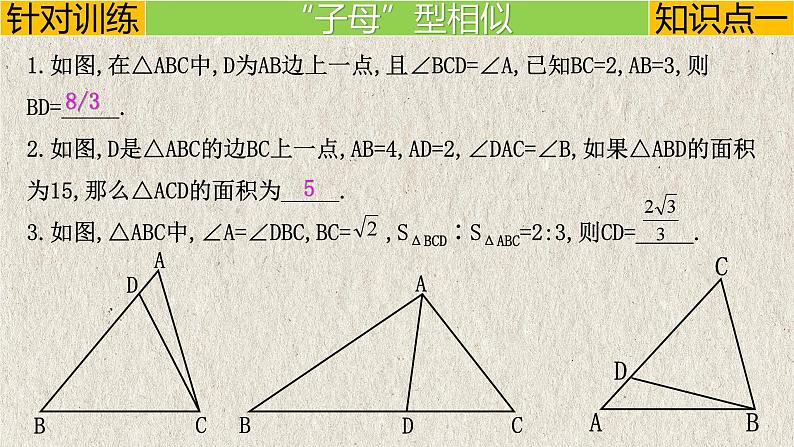
1.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2,AB=3,则BD=_____.2.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为_____.3.如图,△ABC中,∠A=∠DBC,BC= ,SΔBCD∶SΔABC=2:3,则CD=_____.
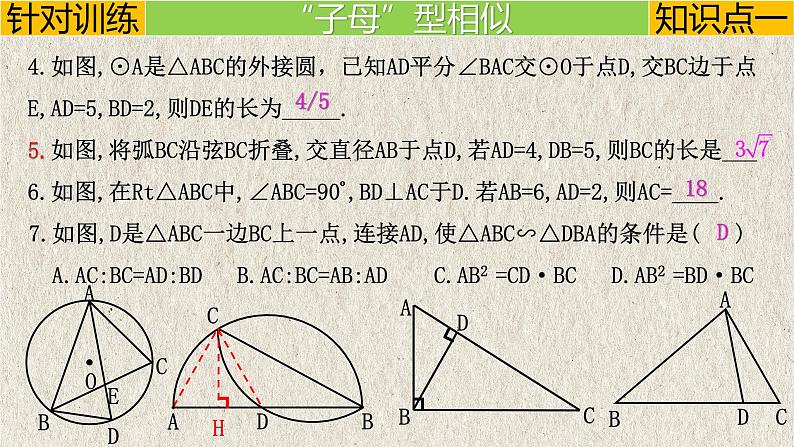
4.如图,⊙A是△ABC的外接圆，已知AD平分∠BAC交⊙O于点D,交BC边于点E,AD=5,BD=2,则DE的长为_____.5.如图,将弧BC沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是___6.如图,在Rt△ABC中,∠ABC=90º,BD⊥AC于D.若AB=6,AD=2,则AC=____.7.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( ) A.AC:BC=AD:BD B.AC:BC=AB:AD C.AB2 =CD·BC D.AB2 =BD·BC
∵∠AEB=∠EAD+∠ADE,∠ADC=∠BDC+∠ADE
∵∠EAB＝∠DAC，
【分析】在Rt△ACB中,∠ACB=90º,∠CAB=30º.
∴∠ADC=∠AFB=60º+90º=150º.
∴△ACD∽△ABF.
连接DF,∴Rt△ACB∽Rt△ADF(一转成双).
在根据勾股定理逆定理可证：△BDF为直角三角形且∠DFB=90º,
【例3】如图,已知AB,CD,EF都与BD垂直,垂足分别是B,D,F,且AB=1,CD=3,那么EF的长是____.
1.如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF,若AB=2,CD=3,则EF=___.2.如图,AB∥DC,AC与BD相交于点E,EF∥DC交BC于点F,CE=5,CF=4,AE=BC,则DC:AB=_____.
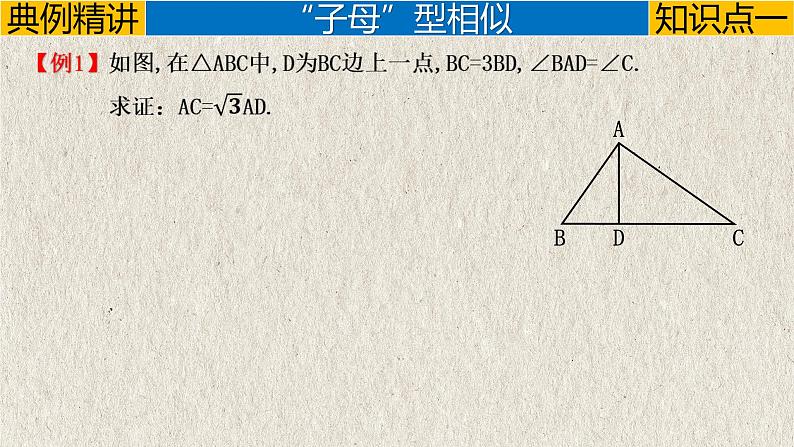
2.在△ABC中,点P为边AB上一点. (1)如图1,若∠ACP=∠B,求证：AC2=AP·AB； (2)如图2,点M为CP的中点,AC=2,∠PBM=∠ACP,AB=3.求BP的长.
【变式】已知:如图,∠ABD=∠C,AD=2且AC=8,求AB长.