


所属成套资源:【单元测试】北师大版(2019)高中数学 选择性必修第二册 单元测试(含答案)
北师大版(2019)高中数学 选择性必修第二册 第一章 空间几何体 A卷基础夯实(Word含答案解析)
展开
这是一份北师大版(2019)高中数学 选择性必修第二册 第一章 空间几何体 A卷基础夯实(Word含答案解析),共11页。
![]() 第一章 空间几何体 A卷 基础夯实-2021-2022学年高一数学人教A版必修2单元测试AB卷【满分:100分】一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知某几何体的三视图如图所示,则该几何体的体积为( )
第一章 空间几何体 A卷 基础夯实-2021-2022学年高一数学人教A版必修2单元测试AB卷【满分:100分】一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知某几何体的三视图如图所示,则该几何体的体积为( )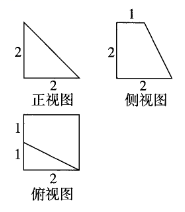 A.2 B.
A.2 B.![]() C.
C.![]() D.42.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A.
D.42.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,已知四边形ABCD的直观图是直角梯形
3.如图,已知四边形ABCD的直观图是直角梯形![]() ,且
,且![]() ,则四边形ABCD的面积为( )
,则四边形ABCD的面积为( )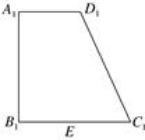 A.3 B.
A.3 B.![]() C.
C.![]() D.64.如图所示的几何体,关于其结构特征,下列说法不正确的是( )
D.64.如图所示的几何体,关于其结构特征,下列说法不正确的是( )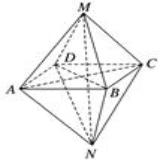 A.该几何体是由两个同底的四棱锥组成的B.该几何体有12条棱、6个顶点C.该几何体有8个面,并且各面均为三角形D.该几何体有9个面,其中一个面是四边形,其余均为三角形5.已知某三棱锥的正视图与侧视图如图所示,则其俯视图可能是( )
A.该几何体是由两个同底的四棱锥组成的B.该几何体有12条棱、6个顶点C.该几何体有8个面,并且各面均为三角形D.该几何体有9个面,其中一个面是四边形,其余均为三角形5.已知某三棱锥的正视图与侧视图如图所示,则其俯视图可能是( )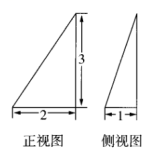
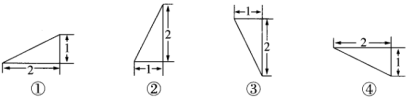 A.①③ B.②④C.①④ D.②③6.已知某几何体的三视图如图所示,则该几何体的体积为( )
A.①③ B.②④C.①④ D.②③6.已知某几何体的三视图如图所示,则该几何体的体积为( )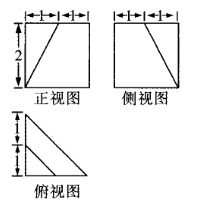 A.4 B.3 C.1 D.
A.4 B.3 C.1 D.![]() 7.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:
7.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:![]() )是( )
)是( )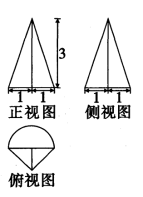 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
8.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )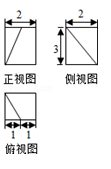 A.9 B.
A.9 B.![]() C.11 D.
C.11 D.![]() 9.已知某几何体的三视图如图所示,则该几何体的表面积为( )
9.已知某几何体的三视图如图所示,则该几何体的表面积为( )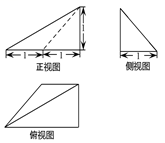 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.已知圆锥的顶点为P,母线PA,PB所成角的余弦值为
10.已知圆锥的顶点为P,母线PA,PB所成角的余弦值为![]() ,PA与圆锥底面所成角为
,PA与圆锥底面所成角为![]() .若
.若![]() 的面积为
的面积为![]() ,则该圆锥的体积为( )A.
,则该圆锥的体积为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题:本题共5小题,每小题5分,共25分.11.菱形ABCD中,
二、填空题:本题共5小题,每小题5分,共25分.11.菱形ABCD中,![]() ,
,![]() ,将
,将![]() 沿BD折起,C点变为E点,当四面体
沿BD折起,C点变为E点,当四面体![]() 的体积最大时,四面体
的体积最大时,四面体![]() 的外接球的面积为________.12.已知棱台
的外接球的面积为________.12.已知棱台![]() .正方形
.正方形![]() 的边长为2,正方形
的边长为2,正方形![]() 的边长为4,平面
的边长为4,平面![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,则棱台
,则棱台![]() 的体积为________.13.在平面四边形PACB中,已知
的体积为________.13.在平面四边形PACB中,已知![]() ,
,![]() ,
,![]() ,
,![]() .沿对角线AB折起得到四面体
.沿对角线AB折起得到四面体![]() ,当PA与平面ABC所成的角最大时,该四面体的外接球的半径为_________.14.两个互相垂直的平面截球O得圆
,当PA与平面ABC所成的角最大时,该四面体的外接球的半径为_________.14.两个互相垂直的平面截球O得圆![]() ,
,![]() ,若圆
,若圆![]() ,
,![]() 的相交弦长为4,则球O表面积的最小值为_______________.15.若圆台的上,下底面半径分别为2,4,高为2,则该圆台的侧面积为_________.三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.16. (10分)已知四棱锥
的相交弦长为4,则球O表面积的最小值为_______________.15.若圆台的上,下底面半径分别为2,4,高为2,则该圆台的侧面积为_________.三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.16. (10分)已知四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() .
.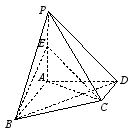 (1)设平面
(1)设平面![]() 平面
平面![]() ,求证:
,求证:![]() ;(2)若E是PA的中点,求四面体PBEC的体积.17. (15分)在底面半径为2高为
;(2)若E是PA的中点,求四面体PBEC的体积.17. (15分)在底面半径为2高为![]() 的圆锥中内接一个圆柱,且圆柱的底面积与圆锥的底面积之比为
的圆锥中内接一个圆柱,且圆柱的底面积与圆锥的底面积之比为![]() ,求圆柱的表面积.
,求圆柱的表面积.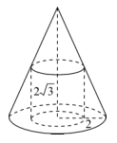
答案以及解析1.答案:C解析:由三视图可知该几何体的直观图为如图所示的多面体ABCDEF,可看作是一个四棱锥和一个三棱锥的组合体,其中四棱锥![]() 的底面是边长为2的正方形,高为2,三棱锥
的底面是边长为2的正方形,高为2,三棱锥![]() 的底面是直角边长为2的等腰直角三角形,高为1,则该几何体的体积
的底面是直角边长为2的等腰直角三角形,高为1,则该几何体的体积![]() ,故选C.
,故选C.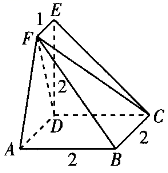 2.答案:A解析:解:恢复后的原图形为一直角梯形,上底为1,高为2,下底为
2.答案:A解析:解:恢复后的原图形为一直角梯形,上底为1,高为2,下底为![]() ,
,![]() .3.答案:C解析:如图,取
.3.答案:C解析:如图,取![]() ,过点
,过点![]() 作
作![]() ,易求得
,易求得![]() ,
,![]() ,故以
,故以![]() 和
和![]() 为坐标轴建立直角坐标系,由直观图原则,B,C与
为坐标轴建立直角坐标系,由直观图原则,B,C与![]() ,
,![]() 重合,然后过点E作
重合,然后过点E作![]() 的平行线,且使得
的平行线,且使得![]() ,即得点A,然后过A作
,即得点A,然后过A作![]() 且使得
且使得![]() ,即四边形ABCD上底和下底边长分别为1,2,高为
,即四边形ABCD上底和下底边长分别为1,2,高为![]() ,故其面积
,故其面积![]() .故选C.
.故选C.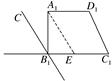 4.答案:D解析:其中ABCD不是面,该几何体有8个面.5.答案:C解析:由正视图与侧视图知,该三棱锥的直观图可为如图(1)、图(2)所示的三棱锥
4.答案:D解析:其中ABCD不是面,该几何体有8个面.5.答案:C解析:由正视图与侧视图知,该三棱锥的直观图可为如图(1)、图(2)所示的三棱锥![]() ,图(1)中
,图(1)中![]() 平面BCD,
平面BCD,![]() ,
,![]() ,
,![]() ,
,![]() ,其俯视图为①,图(2)中
,其俯视图为①,图(2)中![]() 平面BCD,
平面BCD,![]() ,
,![]() ,
,![]() ,其俯视图为④,故选C.
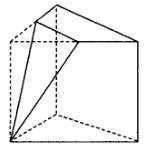
,其俯视图为④,故选C.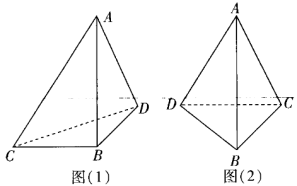 6.答案:D解析:由三视图可知,该几何体为个底面为直角边长为2的等腰直角三角形,高为2的直三棱柱割掉一个底面为直角边长为1的等腰直角三角形,高为2的三棱锥后所剩几何体,如图所示.故该几何体的体积
6.答案:D解析:由三视图可知,该几何体为个底面为直角边长为2的等腰直角三角形,高为2的直三棱柱割掉一个底面为直角边长为1的等腰直角三角形,高为2的三棱锥后所剩几何体,如图所示.故该几何体的体积![]() .
. 7.答案:A解析:由几何体的三视图可得,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长为
7.答案:A解析:由几何体的三视图可得,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长为![]() 的等腰直角三角形,高为3的三棱锥的组合体,故该几何体的体积
的等腰直角三角形,高为3的三棱锥的组合体,故该几何体的体积![]() .8.答案:C解析:由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为
.8.答案:C解析:由三视图可知该几何体是在底面为边长是2的正方形、高是3的直四棱柱的基础上,截去一个底面积为![]() ,高为3的三棱锥形成的,该几何体如图所示.
,高为3的三棱锥形成的,该几何体如图所示.![]() ,所以
,所以![]() .
.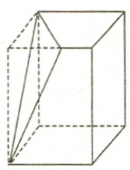 9.答案:A解析:根据三视图知,该几何体是底面为直角梯形的四棱锥
9.答案:A解析:根据三视图知,该几何体是底面为直角梯形的四棱锥![]() ,且侧棱
,且侧棱![]() 底面ABCD;画出图形,如图所示:
底面ABCD;画出图形,如图所示: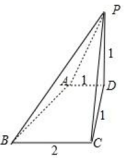 结合图中数据,计算该几何体的表面积为:
结合图中数据,计算该几何体的表面积为:![]()
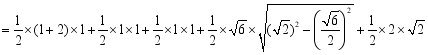
![]()
![]() .10.答案:C解析:如图所示,设底面半径为
.10.答案:C解析:如图所示,设底面半径为![]() ,
,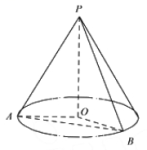
![]() PA与圆锥底面所成角为60°,
PA与圆锥底面所成角为60°,![]() ,
,![]() ,
,![]() 母线PA,PB所成角的余弦值为
母线PA,PB所成角的余弦值为![]() ,
,![]() ,
,![]() ,
,![]() ,故选:C.11.答案:
,故选:C.11.答案:![]() 解析:如图所示,
解析:如图所示,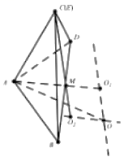 当平面
当平面![]() 平面ABD时,四面体
平面ABD时,四面体![]() 的体积最大,分别从
的体积最大,分别从![]() 和
和![]() 的外接圆圆心
的外接圆圆心![]() ,
,![]() 作其面的垂线,交于点O,即为外接球球心,则易知四边形
作其面的垂线,交于点O,即为外接球球心,则易知四边形![]() 为正方形,由
为正方形,由![]() 知,
知,![]() ,
,![]() ,由正弦定理知
,由正弦定理知![]() ,故
,故![]() ,在
,在![]() 中,
中,![]() ,故四面体
,故四面体![]() 的外接球的面积为
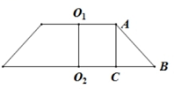
的外接球的面积为![]() .12.答案:28解析:由棱台的体积公式可得
.12.答案:28解析:由棱台的体积公式可得![]() ,所以棱台
,所以棱台![]() 的体积为28.13.答案:
的体积为28.13.答案:![]() 解析:当PA与平面ABC所成的角最大时,最大角为
解析:当PA与平面ABC所成的角最大时,最大角为![]() ,此时平面
,此时平面![]() 平面ABC.在
平面ABC.在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,又
,又![]() ,
,![]() 为直角三角形,
为直角三角形,![]() ,
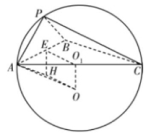
,![]() 平面PAB.如图,设四面体的外接球的球心为O,截面ABC对应圆的圆心为
平面PAB.如图,设四面体的外接球的球心为O,截面ABC对应圆的圆心为![]() ,截面PAB对应圆的圆心为H,E为AB的中点,则球心O到平面PAB的距离为
,截面PAB对应圆的圆心为H,E为AB的中点,则球心O到平面PAB的距离为![]() .设
.设![]() 的外接圆半径为r,由正弦定理可得
的外接圆半径为r,由正弦定理可得![]() ,则
,则![]() .设四面体的外接球半径为R,连接OA,AH在
.设四面体的外接球半径为R,连接OA,AH在![]() 中,
中,![]() ,解得
,解得![]() .
. 14.答案:
14.答案:![]() 解析:设圆
解析:设圆![]() ,
,![]() 的相交弦为AB,球O的半径为R,易知当AB为球O的直径时,R取得最小值,此时球O的表面积最小,为
的相交弦为AB,球O的半径为R,易知当AB为球O的直径时,R取得最小值,此时球O的表面积最小,为![]() .15.答案:
.15.答案:![]() 解析:解:依题意
解析:解:依题意![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以圆台的母线
,所以圆台的母线![]() ,故圆台的侧面积
,故圆台的侧面积![]() .故答案为:
.故答案为:![]() .
. 16.答案:(1)见解析(2)
16.答案:(1)见解析(2)![]() 解析:(1)证明:因为
解析:(1)证明:因为![]() ,
,![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
所以![]() 平面PAB.因为
平面PAB.因为![]() 平面PCD,平面
平面PCD,平面![]() 平面
平面![]() ,所以
,所以![]() .(2)解:
.(2)解:![]() ,
,![]() 平面PAB,所以C,D两点到平面PAB的距离相等.由条件易得
平面PAB,所以C,D两点到平面PAB的距离相等.由条件易得![]() 平面PAB且
平面PAB且![]()
![]() .17.答案:
.17.答案:![]() 解析:因为圆柱的底面积与圆锥的底面积之比为
解析:因为圆柱的底面积与圆锥的底面积之比为![]() ,所以圆柱的底面半径与圆锥的底面半径之比为
,所以圆柱的底面半径与圆锥的底面半径之比为![]() ,所以圆柱的母线长与圆锥的高之比为
,所以圆柱的母线长与圆锥的高之比为![]() ,所以圆柱的底面半径为1,母线长为
,所以圆柱的底面半径为1,母线长为![]() .所以圆柱的表面积
.所以圆柱的表面积![]()






