所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
活动单导学课程苏教版高中数学选择性必修第一册 1.5.1平面上两点间的距离(有答案)
展开这是一份活动单导学课程苏教版高中数学选择性必修第一册 1.5.1平面上两点间的距离(有答案),共6页。
1.5.1 平面上两点间的距离
![]()
1. 探索并掌握平面上两点间的距离公式.
2. 掌握平面上连接两点的线段的中点坐标公式.
3. 运用距离公式和中点坐标公式解决一些简单的问题.
![]()
活动一 | 探究平面上两点间的距离公式 |
1. 回忆初中数轴上两点间的距离公式:
问题1:在平面直角坐标系中,已知点P1(-1,3),P2(3,-2),则它们之间的距离是多少?如何转化为坐标轴上(或平行于坐标轴)的距离问题?
问题2:对于平面上两点P1(x1,y1),P2(x2,y2),它们之间的距离是多少?
思考1
当x1=x2时,P1P2的值是多少?当y1=y2时,P1P2的值是多少?原点O(0,0)与任意一点P(x,y)之间的距离OP的值是多少?
例1 (1) 求A(-1,3),B(2,5)两点间的距离;
(2) 已知A(0,10),B(a,-5)两点间的距离是17,求实数a的值.
活动二 | 探究线段的中点坐标公式 |
问题3:在平面直角坐标系中,若两点P1(-5,-2),P2(3,4),则线段P1P2的中点坐标是什么?如何求得?
问题4:对于平面上两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则点M的坐标是____________.
思考2
已知点P1(x1,y1),P2(x2,y2),M(x0,y0),其中求证:M为P1P2的中点.
例2 已知△ABC的顶点坐标为A(-1,5),B(-2,-1),C(4,7),求BC边上的中线AM的长和中线AM所在直线的方程.

活动三 | 两点间的距离公式和中点坐标公式的应用 |
例3 已知△ABC是直角三角形,斜边BC的中点为M,试建立适当的平面直角坐标系,求证:AM=BC.
![]()
求解这类问题的一般步骤:
(1) 建立平面直角坐标系,用坐标表示有关的量;
(2) 根据距离公式进行有关代数运算;
(3) 把代数结果“翻译”成几何关系.
![]() 已知点A(3,-1),B(,),C(3,4),试判断△ABC的形状.
已知点A(3,-1),B(,),C(3,4),试判断△ABC的形状.
例4 已知直线l:y=x-1.
(1) 求直线l关于点(2,3)对称的直线方程;
(2) 求点P(3,4)关于直线l对称的点Q.
![]() 已知点M(-1,3),N(6,2),点P在x轴上,且使PM+PN取最小值,求点P的坐标.
已知点M(-1,3),N(6,2),点P在x轴上,且使PM+PN取最小值,求点P的坐标.
![]()
1. 已知点M(m,-1),N(5,m),且MN=2,则实数m的值为( )
A. 1 B. 3 C. 1或3 D. -1或3
2. 光线从点A(-3,5)射到x轴上,经x轴反射后经过点B(2,10),则光线从点A到点B的路程为( )
A. 5 B. 2 C. 5 D. 10
3. (多选)已知一条平行于x轴的线段长是5个单位长度,若它的一个端点是A(2,1),则它的另一个端点B的坐标可以是( )
A. (-3,1) B. (7,1) C. (5,1) D. (2,5)
4. (1) 已知两点P(1,-4),A(3,2),则点A关于点P的对称点B的坐标为________;
(2) 点A(2,2)关于直线2x-4y+9=0的对称点的坐标为________.
5. 已知正方形ABCD的边长为4,若E是BC的中点,F是CD的中点,试建立平面直角坐标系,求证:BF⊥AE,BF=AE.
参考答案与解析
【活动方案】
1. 略
问题1:过点P1向x轴作垂线,过点P2向y轴作垂线,两条垂线交于点Q,则点Q的坐标为(-1,-2),且QP1=|3-(-2)|=5,QP2=|3-(-1)|=4.在Rt△P1QP2中,P1P=QP+QP=52+42=41,故P1,P2两点之间的距离为.
问题2:P1P2=
思考1:|y2-y1| |x2-x1|
例1 (1) AB==.
(2) AB==17,
解得 a=±8.
问题3:(-1,1)
问题4:
思考2:略
例2 因为M是线段BC的中点,所以点M的坐标为(1,3).由两点间的距离公式,得AM=2.
由两点式方程得中线AM所在直线的方程为=,即x+y-4=0.
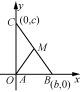
例3 如图,以Rt△ABC的直角边AB,AC所在直线为坐标轴,建立平面直角坐标系,
设B,C两点的坐标分别为(b,0),(0,c).
因为M是BC的中点,
所以点M的坐标为.
由两点间的距离公式,得
AM==,
BC=,所以AM=BC.
跟踪训练 由两点间的距离公式,得
AB==,
AC==5,
BC==.
因为AB=BC,且AC2=AB2+BC2=25,
所以△ABC是以B为直角顶点的等腰直角三角形.
例4 (1) 设M(a,b)为所求直线上的任意一点,其关于点(2,3)的对称点N的坐标为(4-a,6-b).因为点N在直线l上,所以6-b=(4-a)-1,即a-2b+10=0,所以所求直线的方程为x-2y+10=0.
(2) 设点Q(x0,y0),由题意,得PQ⊥l,且PQ的中点在直线l上,
所以解得
所以点Q.
跟踪训练 点M(-1,3)关于x轴的对称点为M′(-1,-3),连接M′N,则直线M′N与x轴的交点即为所求的点P.
直线M′N的方程为=.
令y=0,解得x=,
所以点P的坐标为.
【检测反馈】
1. C 解析:由题意,得=2,解得m=1或m=3.
2. C 解析:点A(-3,5)关于x轴的对称点为A′(-3,-5),则光线从点A到点B的路程即A′B的长,A′B==5,即光线从点A到点B的路程为5.
3. AB 解析:因为AB∥x轴,所以设B(a,1).又AB=5,所以a=-3或a=7.故选AB.
4. (1) (-1,-10) 解析:设点B的坐标为(a,b),则解得故点B的坐标为(-1,-10).
(2) (1,4) 解析:设对称点为A′(m,n),则解得故对称点的坐标为(1,4).
5. 建立平面直角坐标系,如图所示.
则B(4,0),E(4,2),F(2,4),A(0,0).
所以kAE==,kBF==-2,
所以kAE·kBF=×(-2)=-1,即BF⊥AE.
又因为BF==2,AE==2,所以BF=AE.
相关试卷
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.2 直线的两点式方程(有答案),共7页。试卷主要包含了 下列说法中,错误的是, 已知直线l经过点和点.等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.1直线的点斜式方程(有答案),共5页。试卷主要包含了2.1 直线的点斜式方程等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第1章 直线与方程复习(有答案),共8页。试卷主要包含了 梳理本章知识,构建知识网络., 下列说法中,正确的是, 已知点P,直线l等内容,欢迎下载使用。